Задачи к семинару №2
1. Пусть 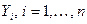 являются независимыми одинаково распределенными случайными величинами с
являются независимыми одинаково распределенными случайными величинами с 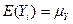 . Покажите, что выборочное среднее
. Покажите, что выборочное среднее 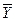 является МНК оценкой генерального среднего.
является МНК оценкой генерального среднего.
Задачи из учебника Стока и Уотсона:
4.6. Покажите, что первое предположение метода наименьших квадратов, т.е. 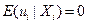 , предполагает, что
, предполагает, что 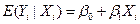 .
.
4.7. Покажите, что 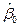 является несмещенной оценкой
является несмещенной оценкой 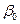 . (Подсказка: Используйте тот факт, что
. (Подсказка: Используйте тот факт, что 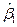 является несмещенной оценкой, как показано в приложении 4.3.)
является несмещенной оценкой, как показано в приложении 4.3.)
4.8. Предположим, что все предположения МНК–регрессии из вставки «Основные понятия 4.3» выполнены, за исключением того, что первое предположение заменяется на предположение 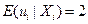 . Какая часть выводов из вставки «Основные понятия 4.4» останется верной? Каковы изменения? Почему? (
. Какая часть выводов из вставки «Основные понятия 4.4» останется верной? Каковы изменения? Почему? (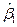 асимптотически нормально распределена со средним значением и дисперсией, заданными во вставке «Основные понятия 4.4»? Что можно сказать о
асимптотически нормально распределена со средним значением и дисперсией, заданными во вставке «Основные понятия 4.4»? Что можно сказать о 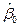 ?
?
4.11. Рассмотрим модель парной линейной регрессии 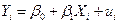 .
.
а. Предположим, вы знаете, что 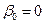 . Выведите формулу оценки наименьших квадратов для
. Выведите формулу оценки наименьших квадратов для 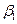 .
.
б. Предположим, вы знаете, что 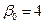 . Выведите формулу оценки наименьших квадратов для
. Выведите формулу оценки наименьших квадратов для 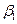 .
.
4.14. Покажите, что линия выборочной регрессии проходит через точку 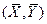 .
.
4.5. Профессор решает провести эксперимент, чтобы измерить как влияет эффект нехватки времени на финальную экзаменационную оценку. Он дает каждому из 400 студентов в его курсе одинаковый итоговый экзамен, но некоторые студенты получают 90 минут, чтобы закончить экзамен, в то время как другие получают 120 минут. Студенты распределяются по группам с разным временем на написание экзаменационной работы случайным образом, основываясь на бросании монеты. Пусть 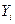 обозначает число результат экзамена i -го студента (
обозначает число результат экзамена i -го студента (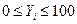 ), а
), а 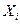 обозначает количество времени, за которое студент закончил экзамен (
обозначает количество времени, за которое студент закончил экзамен (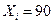 или 120). Рассмотрим модель парной линейной регрессии
или 120). Рассмотрим модель парной линейной регрессии 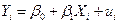 .
.
а. Объясните, что представляет компонента 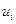 . Почему у разных студентов различные значения
. Почему у разных студентов различные значения 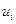 ?
?
б. Объясните, почему 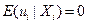 для этой модели регрессии.
для этой модели регрессии.
в. Выполняются ли другие предположения из вставки «Основные понятия 4.3»?
г. Оцененная регрессия имеет вид 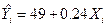 .
.
i. Вычислите предсказанное на основе регрессии значение средней оценки студентов к группе, которая писала экзамен 90 минут. Повторите вычисления для случая 120 минут и 150 минут.
ii. Вычислите предсказанный по регрессии выигрыш в оценке для студента, который получает дополнительные 10 минут на экзамене.
Дополнительные задачи
2. Наблюдались следующие пары значений переменных 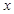 и
и 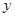 : ( Задача 1.1.2 из УМК-1 )
: ( Задача 1.1.2 из УМК-1 )
(a) 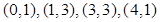 ; (b)
; (b) 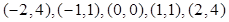 ; (c)
; (c) 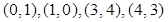 ; (d)
; (d) 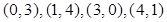 ;
;
(e) 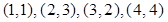 .
.
В каждом из вариантов самостоятельно (“вручную”) постройте диаграмму рассеяния и вычислите выборочный коэффициент корреляции между переменными 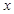 и
и 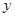 . Проинтерпретируйте полученные значения и сопоставьте их с формой облака точек на диаграммах рассеяния. В любом пункте (например, в пункте (с)) измените масштаб по одной из переменной и вычислите коэффициент корреляции в новой ситуации. [Предложение преподавателя: умножьте x или y сначала на 2, подсчитайте коэффициент корреляции, потом на -2 и тоже подсчитайте коэффициент корреляции]. Изменилось ли значение коэффициента корреляции?
. Проинтерпретируйте полученные значения и сопоставьте их с формой облака точек на диаграммах рассеяния. В любом пункте (например, в пункте (с)) измените масштаб по одной из переменной и вычислите коэффициент корреляции в новой ситуации. [Предложение преподавателя: умножьте x или y сначала на 2, подсчитайте коэффициент корреляции, потом на -2 и тоже подсчитайте коэффициент корреляции]. Изменилось ли значение коэффициента корреляции?
3. Пусть 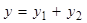 . Пусть методом наименьших квадратов оцениваются модели:
. Пусть методом наименьших квадратов оцениваются модели:
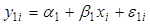 ,
, 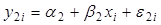 ,
, 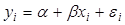 ,
, 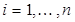 .
.
Покажите, что 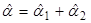 ,
, 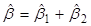 .
.
4. Для модели 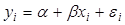 ,
, 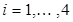 , вычислите оценки коэффициентов по наблюдениям
, вычислите оценки коэффициентов по наблюдениям 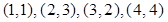 . (Это было сделано ранее.)
. (Это было сделано ранее.)
(а) Используя результаты этих вычислений, найдите оценки коэффициентов “обратной” модели 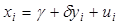 .
.
(б) Вручную постройте график, в котором по оси абсцисс откладываются значения 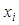 , а по оси ординат – значения
, а по оси ординат – значения 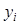 ,
, 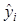 и значения
и значения 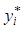 , вычисляемые для значений
, вычисляемые для значений 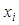 с использованием подобранной ”обратной” модели.
с использованием подобранной ”обратной” модели.
 2017-11-01
2017-11-01 166
166






