Формулировка теоремы: общая нормаль к профилям зубчатых колес, находящимся в зацеплении, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям, т.е.,
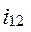
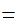
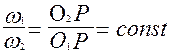 , (10.4)
, (10.4)
где О1, О2 – центры вращения соответственно шестерни и зубчатого колеса; Р – полюс зацепления.
Для доказательства основной теоремы рассмотрим зацепление двух зубьев в некоторый момент времени (рис.5) в точке М со скоростями этих точек 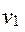
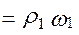
 и
и 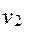
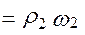 . Проведем через точку касания М общие касательную ТТ и нормаль
. Проведем через точку касания М общие касательную ТТ и нормаль 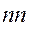 . Очевидно, что условием непрерывности зацепления при вращении колес будет равенство проекций скоростей
. Очевидно, что условием непрерывности зацепления при вращении колес будет равенство проекций скоростей 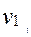 и
и 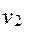 на общую нормаль, т.е.
на общую нормаль, т.е. 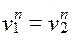 . Обозначая углы векторов с нормалью через
. Обозначая углы векторов с нормалью через 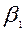 и
и 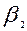 имеем
имеем 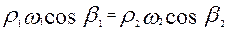 . Откуда:
. Откуда:
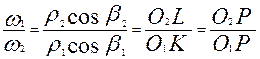 ,
,
что требовалось доказать.  Последнее равенство вытекает из подобия
Последнее равенство вытекает из подобия 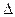 O2PL и
O2PL и 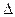 O1PK.
O1PK.
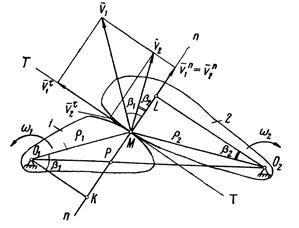
Рис.10.5
Следствие 1. Проекции скоростей на общую касательную ТТ не равны между собой. Поэтому зацепление зубьев происходит со скольжением профилей, от которого возникает износ и потери на трение, зависящие от скорости скольжения 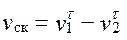 . Скольжения не будет только тогда, когда
. Скольжения не будет только тогда, когда 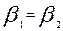 , т.е. в момент зацепления зубьев на линии центров.
, т.е. в момент зацепления зубьев на линии центров.
Следствие 2. Для постоянства передаточного отношения необходимо, чтобы общая нормаль 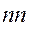 в любой момент зацепления проходила через одну и ту же точку на линии центров, называемую полюсом зацепления Р.
в любой момент зацепления проходила через одну и ту же точку на линии центров, называемую полюсом зацепления Р.
Окружности, проходящие через полюс зацепления, называют начальными (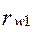 и
и 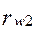 ). Они являются центроидами относительного движения колес.
). Они являются центроидами относительного движения колес.
Основной теореме зацепления и ее следствиям удовлетворяет большое число кривых. Однако с учетом технологических и эксплуатационных требований основной кривой для профилей зубьев является эвольвента круга, предложенная Л. Эйлером в 1754г.
Эвольвента и ее свойства
Эвольвента – это кривая, которую описывает любая точка прямой линии, катящейся без скольжения по окружности, Прямая линия, которая образует эвольвенту, называется производящей, а окружность, по которой она перекатыватся, - основной, ией присваивается индекс b.
Рассмотрим построение эвольвенты. На рис. 6 изображена окружность с центром в точке О.
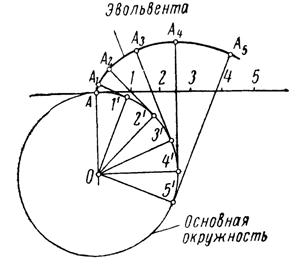
Рис.10.6
К этой окружности проведена касательная в точке А. Будем перекатывать прямую по окружности без скольжения. Для этого от точки А отложим по прямой ряд одинаковых по длине отрезков А – 1, 1 – 2, 2 – 3 и т.д. По окружности от точки А отложим дуги А – 11, 11 – 21, 21 – 31 и т.д., равные этим отрезкам. При перекатывании прямой по окружности без скольжения точка 1 совпадет с точкой 11, точка 2 – с точкой 21 и т.д. Проведем в точках 11, 21, 31,... касательные к окружности (для точного проведения касательной следует сначала провести радиус и затем к нему провести перпендикуляр) и отложим на них от точек касания отрезки 11А1, 21А2, 31А3, …, равные соответственно отрезкам прямой А1, А2, А3,....Соединяя точки А, А1, А2,... плавной кривой, получим эвольвенту.
Прямая линия, которая образует эвольвенту, называется производящей, а окружность, по которой она перекатыватся, - основной, и ей присваивается индекс b.
Эвольвента обладает следующими свойствами:
1) эвольвента начинается на основной окружности и всегда находится
вне ее;
2) образующая прямая нормальна к эвольвенте и является касательной
для основной окружности;
3) Форма эвольвенты зависит только от диаметра db основной
окружности.
Выведем уравнение эвольвенты.
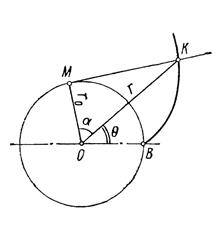
Рис. 10. 7
Пусть координатами какой – либо точки К эвольвенты (рис. 10.7) будут: r – радиус – вектор и 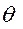 - угол отклонения радиус – вектора от радиуса, проведенного к началу эвольвенты В (на основной окружности). Проведем из точки К касательную к основной окружности радиуса r0. Точку касания М соединим с центром основной окружности О. Угол между лучами ОМ и ОК обозначим через α.
- угол отклонения радиус – вектора от радиуса, проведенного к началу эвольвенты В (на основной окружности). Проведем из точки К касательную к основной окружности радиуса r0. Точку касания М соединим с центром основной окружности О. Угол между лучами ОМ и ОК обозначим через α.
Из треугольника ОМК имеем
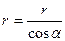 . (10.5)
. (10.5)
Из свойства эвольвенты следует, что

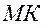 =
= 
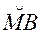 .
.
Но
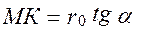 и
и 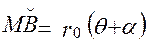 ,
,
тогда
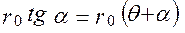
или

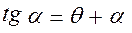 .
.
Решая относительно 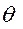 , получим
, получим
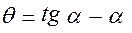 (10.6)
(10.6)
Выражение 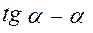 сокращенно обозначается знаком
сокращенно обозначается знаком 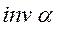 и читается как инволюта
и читается как инволюта 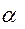 :
:
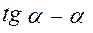
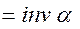 или
или
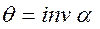 (10.7)
(10.7)
Уравнения (10.6) и (10.7) есть уравнения эвольвенты в полярных координатах.
 2014-01-31
2014-01-31 2114
2114
