Рассмотрим параметры функций:
n=2 – число переменных;
m=4 – число точек определения;
N=16 – число всех функций двух переменных.
Таблица истинности всех функций двух переменных
| Vi | x1,x0 | 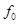
| 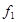
| 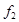
| 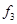
| 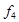
| 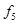
| 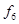
| 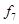
| 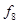
| 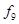
| 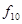
| 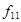
| 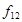
| 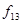
| 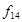
| 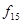
|
| 0 0 | |||||||||||||||||
| 0 1 | |||||||||||||||||
| 1 0 | |||||||||||||||||
| 1 1 |
Значительный интерес представляют невырожденные функции, которые разберем подробно.
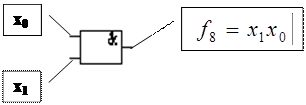
Функция логического умножения (конъюнкция).
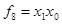 – логическое умножение, описывает работу логического элемента И.
– логическое умножение, описывает работу логического элемента И.
 Vi Vi
| x1,x0 | 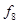
|
| 0 0 | ||
| 0 1 | ||
| 1 0 | ||
| 1 1 |
Функция логического сложения (дизъюнкция)
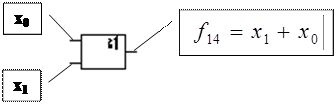
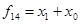 – логическое сложение, описывает работу логического элемента ИЛИ.
– логическое сложение, описывает работу логического элемента ИЛИ.
| Vi | x1,x0 | 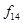
|
| 0 0 | ||
| 0 1 | ||
| 1 0 | ||
| 1 1 |
Функция сложения по модулю два (исключающее ИЛИ, неравнозначность)
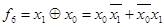 – сложение по модулю два, применяется для арифметического сложения
– сложение по модулю два, применяется для арифметического сложения
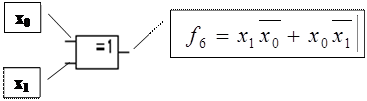 Vi Vi
| x1,x0 | 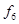
|
| 0 0 | ||
| 0 1 | ||
| 1 0 | ||
| 1 1 |
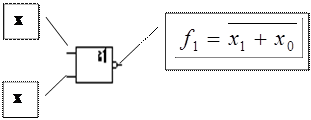
Функция Пирса, логическое сложение с отрицанием, отрицание дизъюнкции (стрелка Пирса, ИЛИ-НЕ)
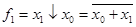 – логическое сложение с отрицанием ИЛИ-НЕ
– логическое сложение с отрицанием ИЛИ-НЕ
 Vi Vi
| x1,x0 | 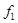
|
| 0 0 | ||
| 0 1 | ||
| 1 0 | ||
| 1 1 |
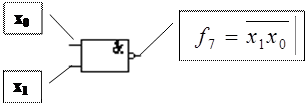
Функция Шеффера, отрицание логического умножения (штрих Шеффера И-НЕ)
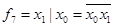 – логическое умножение с отрицанием И-НЕ
– логическое умножение с отрицанием И-НЕ
 Vi Vi
| x1,x0 | 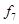
|
| 0 0 | ||
| 0 1 | ||
| 1 0 | ||
| 1 1 |
Функции двух переменных исключительно важны в силу того, что любая логическая функция n переменных может быть получена из них методом суперпозиции – подстановкой этих функций в место переменных в другие функции.
 2014-01-24
2014-01-24 716
716








