Моменты инерции сечений сложной формы

Рис. 4.11

Круг

Рис. 4.9

По формуле параллельного переноса 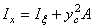, откуда .

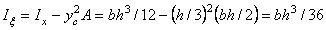Для любых центральных осей 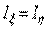, поэтому .

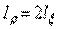Как известно, полярный момент инерции круга равен .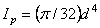

Рис. 4.10

Следовательно, .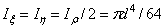

Кольцо ().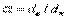

Момент инерции относительно оси 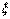(рис.4.11) можно определить как разность моментов инерции наружного и внутреннего круга:

.

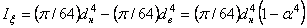Для тонкого кольца существует приближенная формула 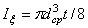, где d _ср – средний диаметр, t - толщина кольца.

Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:

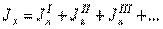, (13)

что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.