Анализ уравнения (15) позволяет перейти к выводу о том, что при заданных 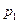 ,
, 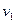 и
и 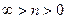 (область существования устойчивых равновесных состояний) величина массового секундного расхода зависит от значения выражения, взятого в квадратные скобки. Легко видеть, что при
(область существования устойчивых равновесных состояний) величина массового секундного расхода зависит от значения выражения, взятого в квадратные скобки. Легко видеть, что при 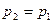 (рис. 2)
(рис. 2) 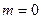 . При
. При 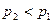 расход газа за счет увеличения расширения газа на участке 1-1 2-2 растет. Однако, при
расход газа за счет увеличения расширения газа на участке 1-1 2-2 растет. Однако, при 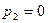
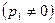 m снова становится равным нулю. Поскольку функция (15), будучи непрерывной, дважды проходит через ноль, то должен существовать максимум массового секундного расхода (рис. 3).
m снова становится равным нулю. Поскольку функция (15), будучи непрерывной, дважды проходит через ноль, то должен существовать максимум массового секундного расхода (рис. 3).

Величина соотношения 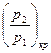 , отвечающая
, отвечающая 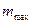 найдется, если взять первую производную от выражения в квадратных скобках уравнения (15) и приравнять ее нулю.
найдется, если взять первую производную от выражения в квадратных скобках уравнения (15) и приравнять ее нулю.
В результате получаем, что для адиабатного процесса изменения состояния критический перепад давлений равен
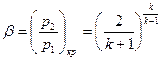 . (16)
. (16)
Естественно, что при подстановке в уравнение (15) вместо 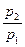 критического перепада давлений мы получим максимальную величину массового секундного расхода. Например, для адиабатного течения, которое чаще всего рассматривается в технических приложениях, имеем
критического перепада давлений мы получим максимальную величину массового секундного расхода. Например, для адиабатного течения, которое чаще всего рассматривается в технических приложениях, имеем
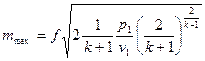 . (17)
. (17)
При дальнейшем уменьшении давления, в окружающей среде 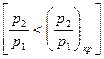 расход остается постоянным, равным
расход остается постоянным, равным  . Это явление получило название "кризис течения".
. Это явление получило название "кризис течения".
Скорость течения газа при 
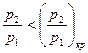 также остается постоянной. Эта скорость называется критической скоростью течения
также остается постоянной. Эта скорость называется критической скоростью течения 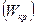 . Уравнение для определения
. Уравнение для определения 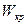 может быть получено, если в (14) вместо
может быть получено, если в (14) вместо 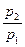 ввести критический перепад давлений
ввести критический перепад давлений 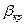
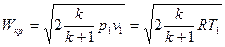 . (18)
. (18)
Разберем физическую картину процесса. По мере движения газа по каналу происходит его расширение, при котором уменьшается 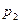 и
и 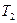 .
.
Снижение 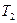 приводит к уменьшению местной скорости звука (9), а скорость потока возрастает. В выходном сечении канала скорость звука в соответствии с (9) будет равна
приводит к уменьшению местной скорости звука (9), а скорость потока возрастает. В выходном сечении канала скорость звука в соответствии с (9) будет равна
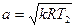 . (19)
. (19)
При кризисе течения скорость потока в выходном сечении определяется (18). Введем в это уравнение вместо 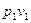 температуру Т. Для адиабатного процесса при
температуру Т. Для адиабатного процесса при 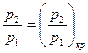
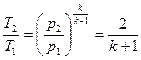
или
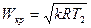 .
.
Таким образом, при достижении критического перепада давлений на выходе из суживающегося сопла скорость потока достигает местной скорости звука. Между тем, давление распространяется тоже со скоростью звука. В результате, уменьшение в окружающей среде давления ниже 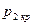 не может подойти к устью сопла, и в последнем устанавливается постоянное давление, равное
не может подойти к устью сопла, и в последнем устанавливается постоянное давление, равное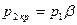 (19). Этим объясняется тот факт, что при
(19). Этим объясняется тот факт, что при 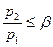
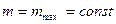
и
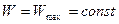 .
.
 2014-01-25
2014-01-25 974
974








