Экспертный метод оценки качества попарным сопоставлением объектов

 

Если сравнение объектов по их качеству осуществлять в табличной форме, то сопоставления и расчеты численных значений экспертных оценок производится по следующей методике.

Во-первых, предпочтение эксперта выражается указанием номера предпочтительного объекта в соответствующей графе таблицы сопоставления, как это показано, например, для шести объектов в табл. 5.1

 

Таблица 5.1

Результаты попарного сопоставления объектов экспертом

Номер эксперта	Номер объекта						Количество предпочтений i-го объекта Ni
	1	2	3	4	5	6
1	х	1	1	1	5	1	4
2		х	2	2	5	2	3
3			х	3	5	3	2
4				х	5	4	1
5					х	5	5
6						х	0

 

Максимально возможное число предпочтений любого из рассматриваемых объектов, полученное от одного из экспертов, равно

 

N_max = m – 1,

где m – количество оцениваемых объектов.

Частота этих предпочтений F_i находится как частное от деления N_i на N_max, т.е.

 

 

Используя для примера данные табл. 5.2, получаем N_max = 6-1=5, а частоты предпочтений, данные экспертом, равны:

 

 

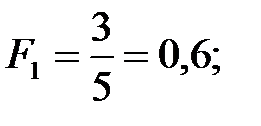
Наибольшее число предпочтений одного объекта С, связанное с количеством объектов экспертов n и экспертизы m, находят из соотношения

 

 

При шести объектах экспертизы и шести экспертах

 

 

Определенный одним экспертом сравнительный показатель качества i-го объекта или весомость по сравнению с другими объектами рассчитывают по формуле (5.43), преобразованной к виду

 

                                            (5.44)

 

где    n – число экспертов в группе;

m – число оцениваемых объектов.

Пусть все показатели частот предпочтений F_j, данные экспертами, сведены в табл. 5.2.

Таблица 5.2

Частоты предпочтений объектов, данные экспертами

Номер эксперта	Частота предпочтений объектов
	F1	F2	F3	F4	F5	F6
1	0,8	0,6	0,4	0,2	1,0	0
2	0,7	0,6	0,3	0,2	0,6	0,1
3	0,6	0,4	0,4	0,3	0,8	0,1
4	0,5	0,5	0,4	0,2	0,8	0
5	0,8	0,4	0,5	0,2	0,7	0
6	0,6	0,3	0,4	0,1	0,6	0
Итого	4,0	2,8	2,4	1,2	4,5	0,2

 

В данном случае результаты экспертизы по определению показателей объектов таковы:

 

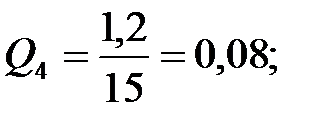
Найдем сумму значений всех показателей весомости рассматриваемых объектов:

 

 

Этот результат свидетельствует о том, что показатели оценены экспертами достаточно точно.

Очевидно, что в приведенном здесь примере итоговый ранжированный ряд объектов рассмотрения по их показателям имеет вид:

 

Q₆ < Q₄ < Q₃ < Q₂ <Q₁ < Q₅.

 

Если сумма показателей весомости существенно отличается от 1, то, чтобы увеличить достоверность оценивания, проводят повторное сопоставление объектов, используя для этого свободную часть таблицы попарного сопоставления. При этом повторное сопоставление производят в хаотическом порядке. В таком случае каждая пара объектов сопоставляется дважды. Такое полное или двойное сопоставление объектов существенно уменьшает случайные ошибки оценок экспертов. Следовательно, двойное сопоставление обладает более высокой достоверностью, чем однократное.

Пусть после двойного сопоставления и установления предпочтений получены результаты оценок одного эксперта, представленные в таблице 5.3.

 

Таблица 5.3

Попарное сопоставление объектов

Номер экспертизы	Номер объекта						Количество предпочтений i -го объекта Ni
	1	2	3	4	5	6
1	х	1	1	1	5	1	7
2	1	х	2	2	5	2	6
3	3	2	х	3	5	3	3
4	1	2	4	х	5	4	3,5
5	5	5	5	4	х	5	8
6	1	2	3	0	5	х	0,5

Примечание. Если сопоставляемые объекты равны между собой, то в таблице это обозначается цифрой 0, но обоим объектам дается по 0,5 предпочтения.

Возможное наибольшее количество предпочтений одного объекта, полученное от одного эксперта, равно:

 

N_max = 2(m - 1),

 

а частота предпочтений

 

 

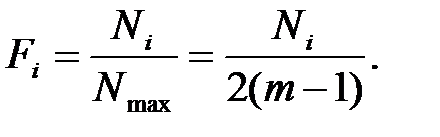
По данным табл. 5.4 находим, что при N_max = 10 у первого эксперта объекты получили такие показатели частот предпочтений:

 

 

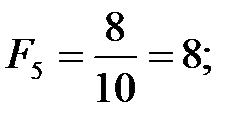
Ранжированный ряд объектов, сопоставленный по оценкам первого эксперта при двойном сопоставлении, такой же, что и при однократном сопоставлении:

 

Q₆ < Q₃ < Q₄ < Q₂ <Q₁ < Q₅.

 

Предположим, что при расчетах F₁ по оценкам всех шести экспертов получены соответствующие значения, приведенные в табл. 5.4.

 

Таблица 5.4

Свод частот предпочтений объектов

Номер эксперта	Частота предпочтений объектов
	F1	F2	F3	F4	F5	F6
1	0,7	0,6	0,3	0,35	0,8	0,05
2	0,6	0,5	0,3	0,2	0,7	0,1
3	0,6	0,4	0,5	0,3	0,8	0,1
4	0,6	0,4	0,4	0,2	0,7	0
5	0,7	0,5	0,5	0,2	0,7	0
6	0,7	0,4	0,3	0,1	0,7	0
Итого	3,9	2,8	2,3	1,35	4,4	0,25

 

Итоговый результат экспертизы всех экспертов, рассчитываемый по формуле (5.44), в примере будет таким:

 

  

 

Сумма всех показателей весомости или значимости (качества) равна:

 

Следовательно, ранжированный ряд по данным экспертизы в целом имеет тот же вид:

 

Q₆ < Q₄ < Q₃ < Q₂ <Q₁ < Q₅.

 

Так получают результаты экспертизы при двойном попарном сопоставлении оцениваемых объектов.