2018-03-09
703
В случае если результат оценивания качества экспертизы представляют в виде ранжированного ряда, численное определение итоговых численных оценок качества состоит в следующем.
Ø Все объекты оценивания (изделия, свойства) нумеруются произвольно.
Ø Эксперты ранжируют объекты по шкале порядка.
Ø Ранжированные ряды объектов, составленные экспертами, сопоставляются.
Пример
Пять экспертов, оценивания семь однотипных объектов Аi и классифицируя их по качеству, составили такие ранжированные ряды по возрастающей шкале порядка:
| эксперт №1 | А5<А3<А2<А1<А6<А4<А7; |
| эксперт №2 | А5<А3<А2<А6<А4<А1<А7; |
| эксперт №3 | А3<А2<А5<А1<А6<А4<А7; |
| эксперт №4 | А5<А3<А2<А1<А4<А6<А7; |
| эксперт №5 | А5<А3<А1<А2<А6<А4<А7; |
Место объекта в ранжированном ряду называется его рангом. Численное значение ранга в ряду возрастающей шкалы порядка увеличивается от 1 до m (m – количество оцениваемых объектов). (В данном примере m=7.)
Ø Определяются суммы рангов Ni каждого из объектов экспертной оценки.
В рассматриваемом примере они таковы:
| N1 | 4+6+4+4+3=21 |
| N2 | 3+3+2+3+4=15 |
| N3 | 2+2+1+2+2=9 |
| N4 | 6+5+6+5+6=28 |
| N5 | 1+1+3+1+1=7 |
| N6 | 5+4+5+6+5=25 |
| N7 | 7+7+7+7+7=35 |
Ø На основании полученных сумм рангов строят обобщенный ранжированный ряд.
Следовательно, в итоге ранжированный ряд, полученный всеми экспертами группы, имеет вид: А5<А3<А1<А2<А6<А4<А7.
Ø Обобщенные экспертные оценки качества группы рассматриваемых объектов экспертизы, т.е. коэффициенты их весомости, рассчитываются по формуле
(5.43)
где m –количество экспертов;
n – число оцениваемых показателей;
- суммарное количество рангов, баллов или предпочтений, полученных i -м объектом от всех j экспертов;
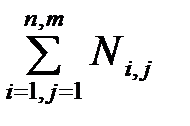- наибольшее число рангов (предпочтений или баллов) всех оцениваемых объектов.
Расчеты по формуле (5.43) для рассматриваемого примера дают следующие результаты:
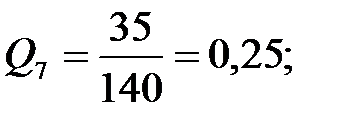
Анализируя полученные экспертным методом оценки качества, можно не только указать, какой объект лучше или хуже других, но и на сколько.
