Интегрирование рациональных дробей

Ситуация 1. Если все корни знаменателя различны.

Задача 28. Вычислить интеграл .

Решение. Разложение на простейшие дроби:

.

Приведём к общему знаменателю: .

Приравняем к исходной дроби. Знаменатели у них и так равны, осталось приравнять числители:   

из этого следует: .

Так как в исходном числителе была только константа 1, то искусственно приписали 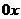, для того, чтобы присутствовали все степени, коэффициенты при которых надо сравнить.

Получается система уравнений:

Решаем систему, складывая уравнения между собой, получится

, т.е. , тогда . Теперь интеграл можно разбить на два интеграла от таких слагаемых:

.

Ответ. , либо в такой форме: .

Задача 29. Вычислить интеграл .

Решение.  = .

, тогда система уравнений для неопределённых коэффициентов:

. Вычитая из 1-го уравнения 2-е, получим:

, т.е. , тогда .

Итак,  =  =

.    

Ответ. .

 

Задача 30. Вычислить интеграл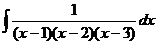    

Решение. В данном случае знаменатель уже разложен в произведение множителей первой степени. Теперь представим дробь в виде суммы:

.

После приведения к общему знаменателю:

 = .

Тогда .

Перегруппируем слагаемые, так, чтобы вынести отдельно вторые степени, первые степени и константы.

.

Отсюда строим систему уравнений:

чтобы её решить, построим расширенную матрицу системы и применим метод Гаусса.

Сначала ко 2-й строке прибавили 1-ю, умноженную на 5,

затем от 3-й отняли 1-ю, умноженную на 6.

Так мы обнулили всё ниже углового элемента .

А теперь к 3-й строке прибавили 2-ю, умноженную на 3:

.

Уже получилась треугольная основная матрица.

Ей соответствует такая система:

, т.е. , тогда , а тогда .

Теперь интеграл сводится к такому виду:

 ,

Ответ.  .

Задача 31. Вычислить интеграл .

Решение. Во-первых, найдём корни знаменателя и разложим его на множители: .

Далее, ,

.

В числителе уже и так был многочлен, а не просто число 1, поэтому не придётся добавлять , ведь все коэффициенты, к которым надо приравнять, в наличии есть.

Приравняем числители:

 

.

Тогда система принимает вид:

, отсюда ,

тогда с учётом этого система примет вид:

, тогда , т.е. , .

.

Ответ. .