Простые формы кристаллов
Анализ элементов симметрии различных кристаллов свидетельствует, что нередко совершенно различные на вид многогранники принадлежат к одному и тому же классу симметрии. Ранее мы уже выяснили, что многогранники в виде куба и октаэдра, несмотря на совершенно разную внешнюю форму, обладают одинаковыми элементами симметрии 3L44L36L29РC.
Можно привести и другие примеры геометрических фигур, которые имеют разную внешнюю форму, но одинаковые наборы элементов симметрии. Подобных примеров, когда одной совокупности элементов симметрии отвечают различные вариации кристаллических многогранников, можно отыскать бесконечное количество.
Отсюда следует, что для полной характеристики внешней морфологии кристаллов недостаточно ограничиваться одними элементами симметрии, а необходимо также принимать во внимание их внешний вид.
По внешнему огранению кристаллы разделяются на две группы. К первой относятся такие кристаллы, которые при своем идеальном развитии состоят из одинаковых и симметрично расположенных граней. Таковы куб, октаэдр, тетраэдры и другие полиэдры. Такого вида многогранники представляют собой простые формы.
Простой формой называется совокупность граней, связанных между собой элементами симметрии, свойственными данному классу симметрии.
Ко второй группе относятся идеальные кристаллы, обладающие различными по очертаниям и величине гранями. Например, “кирпичик” имеет грани трех сортов в виде прямоугольников различного размера, пирамида ограничена гранями двух сортов: треугольными и одной шестиугольной в основании. Грани разной формы, принадлежащие одной геометрической фигуре, называются комбинациями и представляют собой совокупность двух или нескольких простых форм.
Вывод простых форм, присущих тому или иному классу симметрии, основан на размножении плоскости с помощью соответствующей данному классу совокупности операций симметрии. Каждый класс симметрии характеризуется соответствующими ему простыми формами.
Всего существует 47 простых форм кристаллов.
Простые формы кристаллов низшей и средней категории
Для кристаллов низшей и средней категории возможны 22 простые формы (рис. 1.13 – 1.17) из них в сингониях низшей категории встречаются семь типов (рис. 1.13).
Моноэдр - форма, представленная только одной гранью. Пинакоид состоит из двух взаимно параллельных граней. Диэдр образуется двумя пересекающимися одинаковыми по величине и очертанию гранями. Различают диэдр осевой (сфеноид), в котором две грани пересекаются друг с другом по оси симметрии 2-го порядка, и диэдр плоскостной (дома), в котором две грани связаны между

Рис. 1.13. Простые формы низшей категории:
а – моноэдр; б – пинакоид; в,г – диэдры плоскостной (дома) и осевой (сфеноид); д – ромбическая призма; е – ромбические тетраэдры, правый и левый; ж, з – ромбическме пирамида и дипирамида
собой плоскостью симметрии. Ромбическая призма образована четырьмя попарно параллельными гранями. Поперечное сечение такой формы ¾ ромб. В триклинной сингонии встречаются две первые из перечисленных простых форм, в моноклинной ¾ все четыре.
В ромбической сингонии представлены все четыре перечисленные простые формы и к ним добавляются ромбический тетраэдр, ромбические пирамида и дипирамида.
Грани Ромбический тетраэдр сложен четырьмя равными косоугольными треугольникам. Различают два рода ромбических тетраэдров, относящиеся к правой и левой формам. Они соотносятся один к другому как предмет и его зеркальное отражение. Подобные зеркально равные многогранники встречаются и в других сингониях и называются энантиоморфными.
Из рассмотренных простых форм низшей категории в среднюю ¾ переходят только моноэдр и пинакоид. Помимо них, в кристаллах средней категории встречаются 25 новых типов простых форм. Сюда относятся, призмы, пирамиды и дипирамиды (рис. 1.12). Они различаются по форме поперечного сечениям, перпендикулярного главной оси симметрии. Тригональные имеют в сечении равносторонний треугольник (тригон), тетрагональные ¾ квадрат (тетрагон), гексагональные ¾- правильный шестиугольник (гексагон).
В планальных классах симметрии в дополнение к главной оси, имеются еще и плоскости симметрии, проходящие вдоль этой оси. Последние обуславливают появление таких простых форм, как дипризмы и дипирами. Действие продольных плоскостей симметрии заключается в том, что они удваивают каждую грань призмы или пирамиды и, в результате этого, образуются дипризмы и дипирамиды, поперечные сечения которых имеют дитригональный, дитетрагональный или дигексагональны контуры. Удвоение граней не повышает симметрию многоугольника, поскольку две новые грани, замещающие грани призм или пирамид отличаются по величине одна от другой. Например, шесть сторон дитригональной призмы связаны между собой осью L3, а не осью L6.
Особняком стоят тетрагональный тетраэдр, ромбоэдр, тригональный и дитригональный скаленоэдры (рис. 1.15)и серия трапецоэдров (рис. 1.16).

Рис. 1. 14. Призмы, пирамиды и дипирамиды средней категории (верхний ряд – их сечения):
а – тригональная; б – дитригональная; в – тетрагональная; г – дитетрагональная; д – гексагональная; е – дигексагональная

а) б) в) г)
Рис.1.15. Тетрагональный тетраэдр (а); ромбоэдр (б); тетрагональный скаленоэдр; (в) и тригональный скаленоэдр (г)

а) б) г)
Рис.1.16. Трапецоэдры: тригональный (а); тетрагональный (б); гексагональный (в)
Все четыре грани тетрагонального тетраэдра представляют собой равнобедренные треугольники, а его сечение, нормальное к оси L4 ¾ квадрат.
Ромбоэдр относится к простым формам тригональной сингонии и предствляет собой многогранник в виде деформированного куба, вытянутый или сжатый по одной из тройных осей L3. Каждая из его шести граней имеют форму ромба, причем верхняя тройка ромбов повернута относительно нижней тройки ромбов на 600 вокруг главной оси.
Тетрагональный и тригональный скаленоэдры образованы гранями, имеющими форму разносторонних треугольников. Пары их нижних граней расположены симметрично между парами верхних. Тетрагональный скаленоэдр можно представить как простую форму, полученную удвоением граней тетрагонального тетраэдра. Аналогично этому, тригональный скаленоэдр образуется при удвоении граней ромбоэдра. При этом каждая грань ромбоэдра делится пополам вдоль нормальной к ней плоскостью симметрии и поэтому пара верхних граней расположена симметрично между двумя парами нижних.
Группа из трех трапецоэдров, относящихся к простым формам тригональной, тетрагональной и гексагональной сингоний, объединяет многогранники, грани которых пересекают в двух точках главную ось соответственно L3, L4. или L6. Тригональный трапецоэдр имеет шесть граней, тетрагональной ¾ восемь, а гексагональный ¾ двенадцать. В отличие от скаленоэдров с симметричным расположением верхних и нижних граней у трапецоэдров наблюдается несимметричное расположение. Грани трапецоэдров представляют собой четырехугольники с двумя равными смежными сторонами. Из элементов симметрии в трапецоэдрах присутствуют только простые оси. Поскольку нижние и верхние грани у них расположены асимметрично различаются правые и левые трапецоэдры.
Таким образом, низшая и средняя категории содержат в общей сложности 22 простые формы. Из них моноэдр, диэдр, пинакоид, призмы, пирамиды являются незамкнутыми, открытыми формами, а тетраэдры, дипирамиды, трапецоэдры, скаленоэдры, ромбоэдр ¾ закрытыми. Закрытые формы полностью замыкают пространство, а открытые не замыкают его и могут появиться лишь в комбинации с другими простыми формами.
1.8.2. Простые формы кристаллов высшей категории
Ни одна из ранее разобранных простых форм кристаллов низшей и средней категорий в высшую категорию не переходит. Зато в кристаллах кубической сингонии находятся 15 новых типов простых форм.
Среди названий простых форм кристаллов кубической сингонии преобладают сложные, составные. В основу их номенклатуры положены названия несколько основных форм, из которых путем усложнения получаются остальные. К этому названию добавляется наименование и число полученных в результате усложнения новых граней. Исходными простыми формами являются: тетраэдр, гексаэдр (куб) и октаэдр. Усложненные простые формы кубической сингонии получаются путем удвоения, утроения, учетверени и ушестерения числа граней исходных форм.
У кубического тетраэдрачетыре грани в виде правильных треугольников “Надстраивая” на каждой грани тетраэдра по три дополнительных треугольника получим тригон-тритетраэдр. Повторяя эту операцию, но придаавя трем дополнительным гранкам форму четырехугольника и пятиугольника получим тетрагон-тритетраэдр и пентагонтритетраэдр соответственно. И наконец заменим грани тетраэдра шестью дополнительными треугольными гранками получим гексатетраэдр (рис. 1.17).
Октаэдр имеет восемь граней в виде правильных треугольников и в результате их усложнения дает новую серию многогранников, аналогичную тетраэдрической. Утраивая грани октаэдра, получаем последовательно тригон-триоктаэдр, тетрагон-триоктаэдр и пентагон-триоктаэдр с новыми гранями соответственно в форме треугольников, четырехугольников и пятиугольников. Ушестерив октаэдрические грани, приходим к новой простой форме гексоктаэдру (рис. 1.18). Гексоктаэдр самая симметричная простая форма с наибольшим числом. Их у него 48, поэтому в литературе гексоктаэдр часто называют «48-гранником».

а) б) в) г) д)
Рис.1.17. Тетраэдр (а); тригон-тритетраэдр (б); тетрагон-тритетраэдр (в); пентагон-тритетраэдр (г); гексатетраэдр (д)

г) д)
Рис.1.18. Октаэдр (а); тригон-триоктаэдр (б); тетрагон-триоктаэдр (в); пентагонтриоктаэдр (г); гексоктаэдр (д)
Из куба (гексаэдра) (рис. 1.19, а) получается четыре новые простые формы. Надстраивая на гранях куба четырехгранные пирамиды, получаем тетрагексаэдр (рис. 1.19, б). В старых учебниках по кристаллографии такую форму часто называли пирамидальным кубом.

а) б)
Рис. 1.19. Гексаэдр (а); тетрагексаэдр (б)
Притупляя ребра куба гранями, одинаково наклоненными к координатным осям, получаем ромбический додекаэдр или просто ромбододекаэдр. Каждая из 12 граней которого ромбододекаэдра имеет форму ромба (рис. 1.20). Надстраивая на гранях куба двухскатные “крыши”, получаем пентагондодекаэдр, 12 граней которого имеют форму пятиугольников (рис. 1.21, а). Наконец, удваивая каждую грань пентагондодекаэдра, получаем дидодекаэдр (рис. 1.21, б). Каждая из 24 его граней имеет форму трапеции.
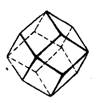
Рис. 1.20. Ромбо додекаэдр
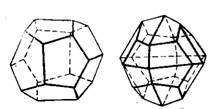
а) б)
Рис.1.21. Пентагон-додекаэдр (а) и дидодекаэдр (б)
В результате, мы перечислили 47 простых форм, возможных в идеальных кристаллах. В таблице 1.5 приведены простые формы для каждого класса симметрии, их названия и символы. Символ грани зависит от класса симметрии и принятой кристаллографической установки. Например, символ (001) в кубической сингонии соответствует грани куба, а в тетрагональной ¾ грани пинакоида или моноэдра. Символа приобретает однозначный смысл только в том случае, когда соблюдаются правила кристаллографической установки или выбора единичной грани.
При росте кристалл часто покрывается комбинациями простых форм. Преимущественное развитие той или иной простой формы или комбинации простых форм зависит от физико-химических условий роста. Наиболее развитыми на кристалле оказываются грани тех простых форм, у которых скорость роста наименьшая и которым соответствуют самые простые символы. От относительного развития граней простой формы зависит габитус (облик) кристалла. Так, кристалл класса m3m может вырасти в виде кубика, столбика, пластинки, игольчатого кристалла с гранями {100}. Чем больше число симметрично эквивалентных граней простой формы, тем сложнее ее символ, но, по закону Гаюи, тем реже встречаются такие формы. Поэтому, как правило, при росте образуются простые формы с малым числом граней и малыми индексами. Однако различные сочетания простых форм дают причудливое многообразие природных форм кристаллов. На рис. 1.22 приведен морфологический ряд постепенного перехода от куба к октаэдру комбинации путем появления на кубе небольших граней октаэдра, которые затем начинают доминировать. Промежуточные формы образованы двумя разными комбинациями куба и октаэдра.

а) б) в) г)
Рис. 1.22. Куб (а), октаэдр (г) и их комбинации (б, в)
На реальных кристаллах покрытых комбинациями простых форм нередко возникают трудности при установлении принадлежности грани той или иной простой форме. На кристаллах алмаза четырехугольные грани тетрагон-триоктаэдра в присутствии гексаэдра видоизменяются в треугольники. Точную принадлежность к простой форме можно надежно установить с помощью гониометра. В его отсутствии для выявления истинных очертаний граней той или иной простой формы в комбинации необходимо мысленно продолжить до взаимного пересечения все грани исследуемой формы, не принимая во внимание грани других форм, входящих в комбинацию.
Для облегчения диагностики простых форм и их кристаллографических символов можно использовать таблицу 1.5.
Таблица 1.5. Символы простых форм в различных классах симметрии
| Символ | Классы и простые формы | ||||||||||||||
| ТРИКЛИННАЯ СИНГОНИЯ | |||||||||||||||
|
hkl | 1 | 1 | |||||||||||||
| Моноэдр | Пинакоид | ||||||||||||||
| МОНОКЛИННАЯ СИНГОНИЯ | |||||||||||||||
|
hkl | 2 | m | 2/m | ||||||||||||
| Диэдр (2) | Ромбическая призма (2) | ||||||||||||||
| h0l | Пинакоид (2) | Моноэдр (1) | Пинакоид (2) | ||||||||||||
| 010 | Моноэдр (1) | Пинакоид (2) | |||||||||||||
| РОМБИЧЕСКАЯ СИНГОНИЯ | |||||||||||||||
|
hkl | 222 | mm2 | mmm | ||||||||||||
| Тетраэдр (4) | Пирамида (4) | Дипирамида (8) | |||||||||||||
| hk0 | Призма (4) | ||||||||||||||
| 0kl; h0l | Призма (4) | Диэдр (2) | Призма (4) | ||||||||||||
| 100; 010 | Пинакоид (2) | ||||||||||||||
| 001 | Пинакоид (2) | Моноэдр (1) | |||||||||||||
| ТРИГОНАЛЬНАЯ СИНГОНИЯ | |||||||||||||||
|
hkil | 3 | 3 | 3m | 32 | 3m | ||||||||||
|
Тригональ-ная пирамида (3) |
Ромбоэдр (6)
| Дитригональ-ная пирамида (6) | Тригональный трапецоэдр (6) | Тригональный скаленоэдр (12) | |||||||||||
| hohl | Тригональ-ная пирамида (3) | Ромбоэдр (6) | |||||||||||||
| hh2hl | Гексагональная пирамида (6) | Тригональная пирамида (6) | Гексагон. ди-пирамида (12) | ||||||||||||
| hki0 |
Тригональная призма (3) |
Гексагональ-ная призма (6) | Дитригональная призма (6) | Дигексагон.. призма (12) | |||||||||||
| 1010 | Тригональная призма (3) | Гексагональная призма (6) | |||||||||||||
| 1120 | Гексагон. призма (6) | Тригональная призма (3) | Гексагон. призма (6) | ||||||||||||
| 0001 | Моноэдр (1) | Пинакоид (2) | Моноэдр (1) | Пинакоид (2) | |||||||||||
| ГЕКСАГОНАЛЬНАЯ СИНГОНИЯ | |||||||||||||||
|
| 6 | 6/m | 6mm | 622 | 6/mmm | 6 | 6m2 | ||||||||
| hkil |
Гексаго-нальная пирамида |
Гексаго-нальная дипира-мида |
Дигекса-гональная пирамида |
Гексагон. трапецо-эдр | Дигекса-гональная дипира-мида |
Триго-нальная дипира-мида | Дитриг. ди-пирамида | ||||||||
| h0hl | Триг. ди-пирамида | ||||||||||||||
| hh2hl | Гекс. пирамида | Гексагональная дипирамида | Гексаг. ди-пирамида | ||||||||||||
| Символ | Классы и простые формы | ||||||||||
| hki0 |
Гексагональная призма | Дигексагональная призма |
Триго-нальная призма | Дитригон. призма | |||||||
| 1010 |
Гексагональная призма | Гексагон. призма | |||||||||
| 1120 | Тригон. призма | ||||||||||
| 0001 | Моноэдр | Пинакоид | Моноэдр | Пинакоид | |||||||
| ТЕТРАГОНАЛЬНАЯ СИНГОНИЯ | |||||||||||
| 4 | 4/m | 4mm | 422 | 4/mmm | 4 | 42m | |||||
| hkl |
Тетраго-нальная пирамида |
Тетраго- нальная дипира-мида |
Дитетра-гональная пирамида | Тетрагон. трапецо-эдр | Дитетра-гон. дипи-рамида |
Тетраго- нальный тетраэдр | Тетрагон. скаленоэдр | ||||
| hhl |
Тетрагонольная дипирамида | Тетрагон.тетраэдр | |||||||||
| h0l | Тетраго-нальная пирамида | Тетрагон. дипира-мида | |||||||||
| hk0 | Тетрагональная призма |
Дитетрагональная призма | Тетрагон. призма | Дитетрагон. призма | |||||||
| 110, 100 | Тетрагональная призма | ||||||||||
| 001 | Моноэдр | Пинакоид | Моноэдр | Пинакоид | |||||||
| КУБИЧЕСКАЯ СИНГОНИЯ | |||||||||||
| 23 | m3 | 43m | 432 | m3m | |||||||
| hkl | Пентагонтри- тетраэдр | Дидодекаэдр | Гексатетраэдр | Пентагонтри- октаэдр | Гексоктаэдр | ||||||
| hhl (h>l) | Тетрагонтри- тетраэдр | Тригонтри- октаэдр | Тетрагонтри- тетраэдр | Тригонтриоктаэдр | |||||||
| hhl(h<l) | Тригонтри-тетраэдр | Тетрагонтри- октаэдр | Тригонтри- тетраэдр | Тетрагонтриоктаэдр | |||||||
| hk0 | Пентагондодекаэдр | Тетрагексаэдр | |||||||||
| 111 | Тетраэдр | Октаэдр | Тетраэдр | Октаэдр | |||||||
| 110 | Ромбододекаэдр | ||||||||||
| 100 | Куб | ||||||||||
 2018-03-09
2018-03-09 1570
1570