Министерство образования Российской Федерации
ФГБОУ ВПО Ивановский государственный химико-технологический университет
Кафедра прикладной математики

ЛАБОРАТОРНАЯ РАБОТА № 5
По дисциплине: «Математические методы и модели в расчётах на ЭВМ»
Тема: Приближенное решение обыкновенных дифференциальных уравнений и систем обыкновенных дифференциальных уравнений.
Вариант 3
Выполнил: ст. группы 2.36
А.А. Машкова__________
Проверил: ст.преп.
С.В. Кулакова___________
Иваново 2011
Задание:
1) Решить дифференциальное уравнение x^2*y’+y^2=0 на отрезке [-1;-0.1] с шагом h=0.1 методом Милна 4-го порядка и заданными начальными условиями y(-1)=1.
Решить систему ОДУ
y’=z
z’=-0.33xz-y
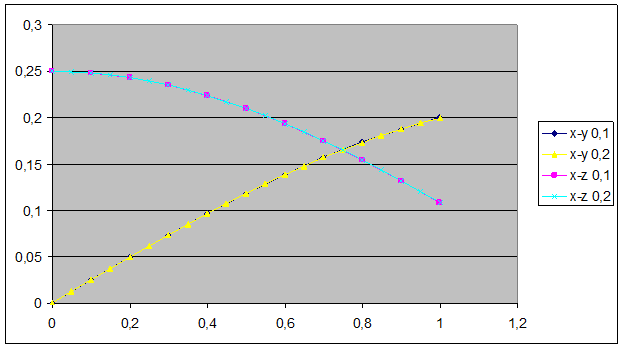
на отрезке [0;1] с шагами h1=0.05, h2=0.1 вторым усовершенствованным методом эйлера с заданными начальными условиями: y(0)=0, z(0)=0.25.
Теоретическая часть
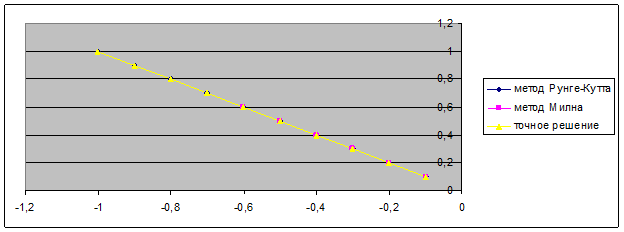
Метод Милна 4-го порядка


2-ой усовершенствованный метод Эйлера (метод Рунге-Кутта 2-го порядка)
Рассмотрим метод Рунге-Кутта второго порядка. В этом методе величины y(i+1) вычисляются по следующим формулам:
Y(i+1) = y(i) + Δy(i)
Δy(i)=Δy(i1)+Δy(i2)
 (см рис 6,6)
(см рис 6,6)
Тогда 

Обозначим  , тогда
, тогда 
Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке (xi, yi) и во вспомогательной точке  , а в качестве окончательного берем среднее из этих направлений.
, а в качестве окончательного берем среднее из этих направлений.
Локальная погрешность третьего порядка:
e=у’’’*h^3/6
Глобальная погрешность второго порядка:O(h^2)
Оценка погрешности с двойным просчетом: (|I(h)-I(h/2)|)/3
Рассчетная часть
Метод Милна 4-го порядка
Определение начального отрезка производится по формуле Рунге-Кутта:

Сначала нужно преобразовать уравнение x^2*y’+y^2=0 в y’=-(y^2/x^2)
K1=h*(-(y^2/x^2))=0.1*(-(1)^2/(-1)^2)=-0.1
K2= h*(-((y+K1/2)^2)/((x+h/2)^2))=0.1*(-(1+(-0.1)/2)^2/((-1+0.1/2)^2))=-0.1
K3= h*(-((y+K2/2)^2)/((x+h/2)^2))= 0.1*(-(1+(-0.1)/2)^2/((-1+0.1/2)^2))=-0.1
K4= h*(-((y+K3)^2)/((x+h)^2))=0.1*(-((1-0.1)^2)/((-1+0.1)^2)=-0.1
Q=abs((K2-K3)/(K1-K2))=0

B3: =B2+D3
C3: =C2+(E2+2*H2+2*J2+L2)/6
E2: =-D2*((C2*C2)/(B2*B2))
F2: =B2+D2/2
G2: =C2+E2/2
H2: =-D2*((G2*G2/F2/F2))
I2: =C2+H2/2
J2: =-D2*((G2*G2/F2/F2))
K2: =C2+J2
L2: =-D2*((K2*K2/B3/B3))
M2: =ABS((H2-J2)/(E2-H2))
Остальные значения находим по методу Милна 4-го порядка:




Погрешность выбираем максимальную, т.е. e=0,01964
D10: =C2+4/3*(2*E3-E4+2*E5)
D11: =C3+4*(2*D4-D5+2*G10)/3
D12: =C4+4*(2*E5-G10+2*G11)/3
D13: =C5+4*(2*G10-G11+2*G12)/3
D14: =F10+4*(2*G11-G12+2*G13)/3
E10: =-C10*D10*D10/B10/B10
F10: =C4+(E4+4*E3+E10)/3
F11: =C5+(E5+4*G10+E11)/3
F12: =F10+(G10+4*G11+E12)/3
G10:= =-C10*F10*F10/B10/B10
H10: =ABS(F10-D10)/29
Программа на Паскале.
Program Miln;
Uses Crt; const n=10;
Var
x0,y0,z0,h:real;
k1,k2,k3,k4:real;
eps,abs_pogr:real;
ypr,ykor,x,y: array [0..n] of real;
i:integer;
function f1(xa,ya:real):real;
Begin
f1:=-ya*ya/xa/xa;
end;
Begin
Clrscr;
eps:=0.001;
x0:=-1;
y0:=1;
h:=0.1;
x[0]:=x0;
y[0]:=y0;
i:=0;
{ Gotovim 1-e 3 tochki po metodu runge-kutta }
while i<=3 do
begin
k1:=h*f1(x[i],y[i]);
k2:=h*f1(x[i]+h/2,y[i]+k1/2);
k3:=h*f1(x[i]+h/2,y[i]+k2/2);
k4:=h*f1(x[i]+h,y[i]+k3);
y[i+1]:=y[i]+(k1+2*k2+2*k3+k4)/6;
x[i+1]:=x0+i*h;
i:=i+1;
end;
i:=4;
while x[i]<=x0+i*h{eps> abs_pogr} do
begin
{ etap prognoza i korrektsii}
ypr[i]:=y[i-4]+(4*h)/3*(2*f1(x[i-3],y[i-3])-f1(x[i-2],y[i-2])+2*f1(x[i-1],y[i-1]));
ykor[i]:=y[i-2]+(h/3)*(f1(x[i-2],y[i-2])+4*f1(x[i-1],y[i-1])+f1(x[i],ypr[i]));
abs_pogr:=abs(ykor[i]-ypr[i])/29;
if abs_pogr>eps then
y[i]:=ykor[i]
Else
y[i]:=ypr[i];
i:=i+1;
end;
WriteLn;
for i:=0 to 10 do
begin
WriteLn(x[i]:10:4,' ',ykor[i]:10:4,' ');
end;
Readln;
end.
Второй усовершенствованный Эйлера.

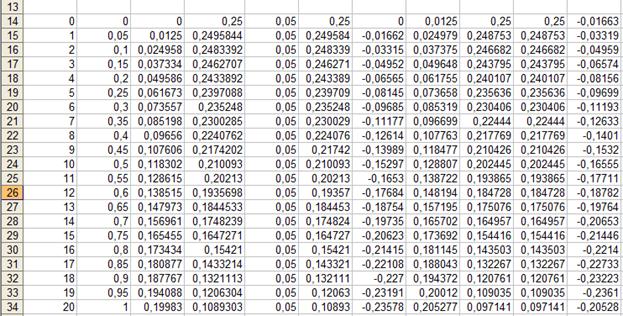
Погрешность высчитывается с помощью двойного просчета:

Выбираем максимальную погрешность:e= 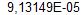
h=0.1
F0=z0=0.25
V0=-0.33*x0*z0-y0=-0.33*0*0.25-0=0
Y’1=y0+h*f0=0+0.1*0.25=0.025
Z’1=z0+h*v0=0.25+0.1*0=0.25
F’1=z’1=0.25
V’1=-0.33*x1*z’1-y’1=-0.03325
Y1=y0+h*(f+f’)/2=0.025
Z1=z0+h*(v+v’)/2=0.2483375
F1=z1=0.248338
V1=-0.33*x1*z1-y1=-0.0332
Y’2=y1+h*f1=0+0.1*0.25=0.049834
Z’2=z1+h*v1=0.25+0.1*0=0.245018
F’2=z’2=0.245018
V’2=-0.33*x2*z’2-y’2=-0.066
Y2=y0+h*(f+f’)/2=0.049668
Z2=z1+h*(v+v’)/2=0.2433775
Аналогичные вычисления проводятся с h=0.05
F0=0,25
V0=0
Y’1=0,0125
Z’1=0,25
F’1=0,25
V’1=-0,01663
Y1=0
Z1=0,25
F1=0,249584
V1=-0,01662
Y’2=0,024979
Z’2=0,248753
F’2=0,248753
V’2=-0,03319
Y2=0,0125
Z2=0,2495844
Вычисление погрешности: е=|Y(h)-Y(h/2)|/3
E1(0)=0-0=0
E2(0)=0.25-0.25=0
E1(1)=0.05-0.049668=0.000111
E2(1)=0.24335-0.2433775= 9,16542E-06
Из погрешностей выбираем максимальную для данной системы ОДУ::e= 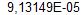
Формулы в excel:
С3: =C2+E3*(F2+J2)/2
D3: =D2+E3*(G2+K2)/2
F2: =D2
G2: =-0,33*B2*D2-C2
H2: =C2+E2*F2
I2: =D2+E2*G2
J2: =I2
K2: =-0,33*B3*I2-H2
M2: =ABS(C14-C2)/3
N2: =ABS(D14-D2)/3
Программа на Паскале
program eiler;
function f(z:real):real;
Begin
f:=z;
end;
function p(x:real;y:real;z:real):real;
Begin
p:=-0/33*x*z-y;
end;
Var
h:real;
x:real;
y1:real;
y2:real;
z1:real;
z2:real;
Begin
h:=0.1;
while h<=0.2 do
begin
y1:=0;
z1:=0.25;
x:=0;
writeln('h= ',h:1:1);
while x<1 do
begin
y2:=y1+h*f(z1);
z2:=z1+h*p(x,y1,z1);
y2:=y1+h/2*(f(z1)+f(z2));
z2:=z1+h/2*(p(x,y1,z1)+p(x,y2,z2));
z1:=z2;
y1:=y2;
x:=x+h;
writeln('x= ',x:2:4,' y= ',y2:2:4,' z= ',z2:2:4);
end;
h:=h+0.1;
end;
readln;
end.

Вывод:
Многошаговые методы дают нам большую точность при вычислении ОДУ и ситем ОДУ по сравнению с одношаговыми. Но существенный недостаток многошаговых методов заключается в большом объеме вычислений, к тому же нам придется сначала находить первые 3 точки одношаговым методом. Многошаговые методы построены путем интерполирования по нескольким соседним точкам, для их использования необходимо знать значение функции y(x) в нескольких предыдущих точках. Достоинство многошаговых методов состоит в том, что независимо от порядка метода для вычисления значения функции y(x) в одной точке требуется один раз вычислить функцию f(x, y).
 2018-02-13
2018-02-13 411
411






