2018-02-13
188
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ М-13
Определение коэфицента внутреннего трения жидкости
Методом Пуазейля
Исполнитель:
студент группы Э7А40 А. В. Кобеев
(подпись)
Руководитель М.И. Чебодаев
(подпись)
(дата)
Томск – 2004
Цель работы: определение коэффициента внутреннего трения методом протекания жидкости по капилляру.
Приборы и принадлежности: сосуд с тубусом и капиллярной трубкой, исследуемая жидкость, штатив, стакан, линейка, секундомер, весы с разновесами, образцы капилляра, измерительный микроскоп.
Краткое теоретическое содержание работы
С молекулярной точки зрения происхождение сил внутреннего
трения объясняется следующим образом. При наличии упорядоченного движения молекул су скоростями V=V(x), молекулы лежащие в верхних, быстрых, слоях обладают большим упорядоченным количеством движения (большей скоростью), чем молекулы, лежащие под ними. Переходя за счет непрерывного теплового хаотического движения в нижние слои, молекулы передают часть своего упорядоченного количества движения молекулам нижних слоев. Это проявляется в том, что на газ (или жидкость), расположенный в нижних слоях, действует сила, направленная в сторону скорости V. Аналогично, более медленные молекулы, попадая в верхние слои, при столкновениях отнимают часть упорядоченного количества движения у молекул, расположенных над ними. В результате газ в верхних слоях испытывает тормозящую силу, направленную против скорости V. Эти силы и являются силами внутреннего трения между слоями газа, движущимися с различными скоростями, и направлены касательно слоям. Как показывает опыт, количество движения 
, приносимое из слоя в слой, определяется уравнением (закон Ньютона)
где - количество движения (импульс), переносимое из слоя в слой, 
- коэффициент внутреннего трения или вязкости, зависящий от свойств газа, 
- разность скоростей слоев, расположенных друг от друга на расстоянии dx, 
- градиент скорости направленного движения молекул (слоев) вдоль оси х, dS - малая площадка прикосновения слоев, через которую переносится , dt - время, течение которого переносится .
Градиентом (grad) физической величины навивают вектор, характеризующий быстроту изменения этой величины вдоль данной оси на единицу длины. Направлен grad в сторону наибольшего возрастания этой величины. Знак минус в означает, что импульс переносится в направлении уменьшения скорости, так как градиент скорости направлен вверх, т.е. в сторону возрастания V, а перенос импульса идет вниз, т.е. в сторону убывания скорости V.
Изменение количества движения по второму закону Ньютона равно импульсу силы Fdt:
На основании выше сказанного сила внутреннего трения равна
где dV - разность скоростей двух слоев, находящихся на расстоянии dx. Выразим коэффициент трения:
Из этого следует, что коэффициент внутреннего трения (вязкости) численно равен силе, действующей на единицу площади слоя при градиенте скорости, равном единице.
Расчетные формулы.
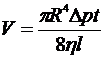- формула Пуазейля. Где l – длина трубки и R – ее радиус, 
- разность давлений на концах трубки, t – время вытекания жидкости, Н – средняя разность высот уровней
, где 
- высота уровня жидкости от стола в конце опыта, 
- высота уровня жидкости от плоскости стола в начале опыта, h – высота капилляра.
Среднее давление, под которым вытекает жидкость:
где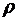 
– плотность жидкости, g – ускорение свободного падения.
где R - радиус капилляра, Н – средняя разность высот уровней, d – плотность жидкости, g – ускорение свободного падения, t – время истечения жидкости, l – длинна трубки, М – масса вытекшей жидкости.
,где 
- среднеквадратичная ошибка среднеарифметического величины 
; N – количество измерений
,где 
-случайная погрешность; 
– коэффициент Стьюдента
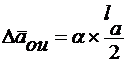, где 
- ошибка однократного измерения величины ; 
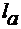– точность измерительного прибора; 
=0,95- доверительный коэффициент
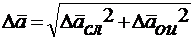,где 
- общая ошибка величины
,где 
- погрешность косвенных измерений
