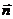В пространстве
| На плоскости | В пространстве | |
| По точке А и направляющему вектору p, векторные параметрические | ||
|
| ||
| По точке А и направляющему вектору p, параметрические в координатной форме | ||
|
| ||
| По точке А и направляющему вектору p,канонические | ||
|
| ||
| По двум точкам А и В, векторные параметрические | ||
|
| ||
| По двум точкам А и В, параметрические в координатной форме | ||
|
| ||
| По двум точкам А и В, канонические | ||
|
| ||
| По точке А и нормальному вектору | ||
|
| ||
Далее продолжите таблицу самостоятельно, внося в нее другие полученные Вами уравнения прямой на плоскости
При подготовке к защите необходимо усвоить
- определение уравнения множества точек (геометрической фигуры);
- необходимые и достаточные условия коллинеарности двух векторов и соответственно условия принадлежности трех точек одной прямой;
- способы задания прямой на плоскости и в пространстве;
- научиться для каждого способа задания получить уравнение прямой, записывая в каждом случае условие принадлежности текущей точки заданной прямой этой прямой;
- запомнить все уравнения прямой линии на плоскости и в пространстве и геометрический смысл параметров каждого уравнения;
- уметь составить уравнение прямой по элементам, которые эту прямую однозначно определяют;
- научиться докладывать и оценивать результаты своей работы, отстаивать свою точку зрения, выступать в качестве экспертов;
 2018-02-13
2018-02-13 154
154