Примерный характер вопросов в билетах

1. Предел и непрерывность.
     Задачи вычислительного характера
   1. Ограничена ли данная последовательность х_n, n=1,2,…?.
   2. Найти lim х_n или доказать, что он не существует;
   3. Дана функция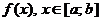 . Найти точки разрыва функции  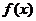или доказать, что
      их нет.
   4. Укажите какой-нибудь интервал , на котором для данной функции существует обратная функция.
   5. Найти область определения суперпозиции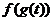 , где 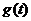определена на заданном
     отрезке [c; d].
    Задачи и вопросы теоретического характера
    Функцияопределена формулой .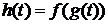
   1. Будет ли функция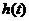 непрерывной, если 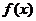и 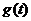 непрерывны?
   2. Будет ли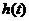 монотонной, есл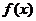и и 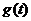монотонны?
   3. Каков характер монотонности функции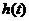 , есл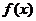и
                      и 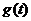 возрастающие;
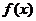                      и 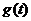 убывающие;
                    одна из них возрастающая, а другая убывающая.
   4. Равносильны ли следующие два утверждения: а)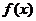 не имеет конечного предела
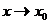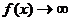      при  ; б)  при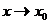
   5. Равносильны ли следующие два утверждения: а)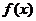  непрерывна в точке ;
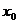   б)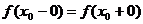  

Производная и дифференциал.
Задачи вычислительного характера

1. Найти на графике функции 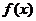точку, в которой касательная параллельна данной прямой.

2..Даны две дифференцируемые функции. Найти тангенс угла, образованного графиками этих  функций в точке их пересечения.

3. Дифференцируема ли 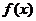 в заданной точке?

4.  Каков порядок разности 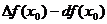 относительно ?

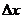5.  Используя дифференциал подходящей функции, вычислить приближенно одно из выражений вида: ,

6. Разложить функцию по формуле Тейлора (выписать 3-4 слагаемых).

Задачи и вопросы теоретического характера

1. Дифференцируема ли функция  в точке 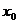, если  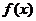диференцируема
в точке 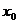и  ?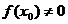

2. Тот же вопрос, если .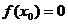

3. Приведите пример функции, непрерывной, но не дифференцируемой в некоторой точке.

4. Приведите пример функции, которая не дифференцируема в некоторой точке 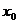, но при этом ее график имеет касательную в точке .

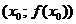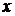5. Останется ли верной формула , если в ней заменить на дифференцируемую функцию  ?

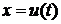С. Исследование функции.
Задачи вычислительного характера

 

1. Функция задана явно или параметрически. Требуется найти:
точки локального экстремума функции;
точку на графике, в которой производная имеет локальный экстремум;
точку на графике, в которой касательная не существует;
интервалы выпуклости функции;
асимптоты (или доказать, что их нет).

2. Найти уравнение касательной плоскости к графику заданной функции в заданной точке и вычислить углы между плоскостью и осями ОХ и ОУ.

3. В какой точке график функции 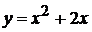имеет наибольшую кривизну?

4. Есть ли на графике точка, в которой кривизна наименьшая?
 
 Задачи и вопросы теоретического характера

1. Может ли дифференцируемая на (a; b) функция иметь на (a; b) более одного минимума
и при этом ни одного максимума?

2. Верно ли, что из 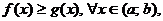 следует 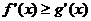? А обратное утверждение?

3.  Будет ли четной производная четной функции? Тот же вопрос для нечетной?

4.   Верно ли обратное утверждение?

5. Будет ли периодической 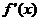, если 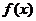периодическая функция?

6.   Будет ли периодической 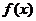, если известно, что  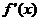периодическая?

7.  Будет ли 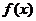 монотонной в малой окрестности точки 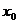, если  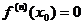при n =1, 2,   а 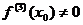? Указание: нужно использовать формулу Тейлора.

8.  Будет ли 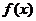 монотонной в малой окрестности точки 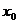, если  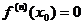при n =1, 2, 3, а ?

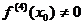9. Те же вопросы относительно выпуклости .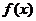

10. Пусть графики дифференцируемых функци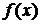й  и 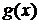 пересекаются в точке 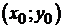.    Чему тогда равен  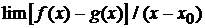при  ?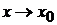

11. Пусть прямая 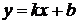 пересекает график дифференцируемой функции  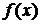и в точке 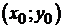. Обозначим 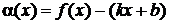. Очевидно, при любом значении коэффициента 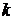функция 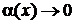при 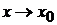. При каком значении 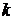бесконечно малая 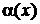будет иметь более высокий порядок, чем ?

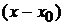12. Приведите пример функции, у которой график имеет разные асимптоты 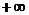на  и на .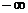

13. Чему равна кривизна графика в точке перегиба?       

Что нужно знать и уметь для успешной сдачи экзамена

                       Определения основных понятий

1. Числовые множества: ограниченность, супремум, инфимум.
2. Предел последовательности и предел функции.
3. Односторонние пределы.
4. Бесконечно малые и бесконечно большие.
5. Непрерывность.
6. Производная.
7. Дифференциал.
8. Возрастающие и убывающие функции.
9. Выпуклость.
10. Экстремум.
11. Первообразная и неопределенный интеграл.

 

              Теоремы, свойства, формулы
 ( доказательства необходимы тем, кто претендует на 4 и 5 ) 

1. Теорема о вложенных отрезках.
2. Теорема Вейерштрасса о выборе сходящейся подпоследовательности.
3. Основные теоремы о пределах.
4. Признаки существования предела последовательности.
5. Сравнение бесконечно малых.
6. Сравнение бесконечно больших.
7. Замечательные пределы.
8. Теоремы о функциях, непрерывных на отрезке.
9. Классификация точек разрыва.
10. Геометрический смысл производной.
11. Связь между непрерывностью и дифференцируемостью.
12. Теорема Лагранжа.
13. Правило Лопиталя.
14. Признаки убывания и возрастания.
15. Необходимое условие экстремума.
16. 1-е достаточное условие экстремума.
17. 2-е достаточное условие экстремума.
18. Признаки выпуклости.
19. Кривизна кривой.
20. Геометрический смысл дифференциала.
21. Инвариантная форма дифференциала.
22. Формула Тейлора.
23. Таблица интегралов.