Первичная обработка данных

ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ

 

Проверил:                              Выполнил:                

студент 2-го курса ФБО

Байда Г.П.

Учебный шифр:

                                                        10-11-ЗЭТ-930М

                                                            

 

 

 

 

                                                                

 

 

2011/2012 учебный год

Лабораторная работа № 1

ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ

При проведении экспериментов фиксировались значения случайной величины X, характеризующей время простоя оборудования в ожидании ремонта (в часах).

Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины Х.

1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке возрастания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.

 

Таблица 1 – Расчетная таблица

Номер п/п	Выборка, час.	Вариацион-ный ряд, , час.
1	26,5	1,08	-9,4463	89,2316
2	10,4	1,22	-9,3063	86,6063
3	9,45	1,72	-8,8063	77,55
4	9,27	1,76	-8,7663	76,8471
5	16,8	1,87	-8,6563	74,9307
6	1,22	1,99	-8,5363	72,8676
7	13,2	2,43	-8,0963	65,5493
8	1,99	2,5	-8,0263	64,4207
9	6,6	3,01	-7,5163	56,494
10	10,4	5,26	-5,2663	27,7334
11	2,43	5,7	-4,8263	23,2927
12	7,16	6,49	-4,0363	16,2913
13	1,72	6,6	-3,9263	15,4154
14	20,3	6,67	-3,8563	14,8707
15	23,8	7,16	-3,3663	11,3316
16	16,8	8,13	-2,3963	5,74201
17	11,3	8,59	-1,9363	3,74906
18	3,01	9,13	-1,3963	1,94951
19	8,59	9,14	-1,3863	1,92169
20	1,08	9,2	-1,3263	1,75894
21	12,4	9,27	-1,2563	1,57816
22	33,7	9,45	-1,0763	1,15831
23	9,13	9,63	-0,8963	0,80326
24	6,49	9,85	-0,6763	0,45731
25	9,2	10,4	-0,1263	0,01594
26	11,9	10,4	-0,1263	0,01594
27	9,63	11,3	0,77375	0,59869
28	9,14	11,9	1,37375	1,88719
29	22,4	12,4	1,87375	3,51094
30	2,5	13,2	2,67375	7,14894
31	5,26	14,6	4,07375	16,5954
32	14,6	14,9	4,37375	19,1297
33	14,9	16,8	6,27375	39,3599
34	5,7	16,8	6,27375	39,3599
35	6,67	20,3	9,77375	95,5262
36	1,87	22,4	11,8738	140,986
37	23,8	23,8	13,2738	176,192
38	1,76	23,8	13,2738	176,192
39	9,85	26,5	15,9738	255,161
40	8,13	33,7	23,1738	537,023
Итого	421,05	421,05

 

 

2) Вычисляю размах выборки:  =33,7- 1,08= 32,62.

 

 

3) Длина интервала = =  = 5,15989.

 

4) границы интервалов: 

= 1,08,  

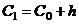=1,08+5,15989= 6,23989,   

= 6,23989+5,15989= 11,39978,

= 11,39978+5,15989= 16,55967, 

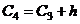= 16,55967+ 5,15989= 21,71956,

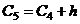= 21,71956+ 5,15989= 26,87945,

= 26,87945+ 5,15989= 32,03934, 

= 32,03934+ 5,15989= 37,19923 .

 

 

5) Строю интервальный статистический ряд:

 

 

Таблица 2 – Интервальный статистический ряд

 

Границы интервалов , час.	Частоты	Частости
[1,08; 6,23989)	11	11/40
[6,23989; 11,39978)	16	16/40
[11,39978; 16,55967)	5	5/40
[16,55967; 21,71956)	3	3/40
[21,71956; 26,87945)	4	4/40
[26,87945; 32,03934)	0	0/40
[32,03934; 37,19923)	1	1/40
Итого	40	1

 

6) Вычисляю числовые характеристики:

В качестве оценки математического ожидания используется среднее арифметическое  наблюденных значений. Эта статистика называется выборочным средним.

      .                  

 

Оценка моды случайной величины.

Как видно из таблицы интервального статистического ряда, имеется два интервала, на которых случайная величина принимает наибольшее значение. Интервалы разделяются в точке 8,819835. Эту точку и принимаю за моду.

=8,819835.

 

Для определения выборочного значения медианы используется вариационный ряд. В качестве оценки медианы  принимают средний (т. е. 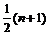-й) член этого ряда, если значение n – нечётно и среднее арифметическое между двумя средними (т. е. между -м и -м) членами этого ряда, если n – чётно. В нашем случае объем выборки = 40 - четное, т.е. в качестве оценки медианы приму 

 = .

В качестве оценки дисперсии используется статистика = .

 

Оценка среднего квадратического отклонения  = .

 

7) Строю гистограмму частот:

 

Рисунок 1 – Гистограмма частот

 

Вывод. В результате исследования выборки значений непрерывной случайной величины, характеризующей время простоя оборудования в ожидании ремонта, получили следующие результаты, час: минимальное время простоя – 1,08, максимальное – 33,7, среднее значение времени простоя оборудования – , наиболее вероятное время простоя оборудования 8,819835, средневероятное – , среднеквадратическое отклонение времени простоя оборудования от среднего значения составило .