Т Е С Т № 34
9.1.2.2
Пусть 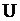 – достоверное событие,
– достоверное событие, 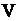 – невозможное событие. Для произвольного события
– невозможное событие. Для произвольного события 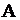 событие
событие 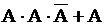 равно
равно
+1. 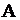 ; 2.
; 2. 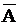 ; 3.
; 3. 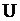 ; 4.
; 4. 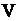 .
.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 36
9.1.2.1
Пусть 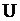 – достоверное событие,
– достоверное событие, 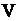 – невозможное событие. Для произвольных событий
– невозможное событие. Для произвольных событий 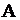 и
и 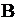 событие
событие 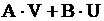 равно
равно
1. 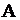 ; +2.
; +2. 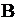 ; 3.
; 3. 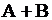 ; 4.
; 4. 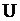 .
.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 37
9.1.2.2
Пусть 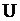 – достоверное событие,
– достоверное событие, 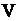 – невозможное событие. Для произвольного события
– невозможное событие. Для произвольного события 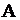 событие
событие 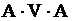 равно
равно
1. 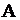 ; +2.
; +2. 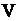 ; 3.
; 3. 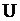 ; 4.
; 4. 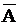 .
.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 38
9.1.2.1
Известно, что при подбрасывании игрального кубика выпало чётное число очков. Вероятность того, что выпало 6 очков, равна
1. 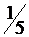 ; 2.
; 2. 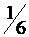 ; +3.
; +3. 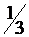 ; 4.
; 4. 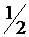 .
.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 39
9.1.2.4
Для произвольного события 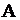 вероятности событий
вероятности событий 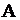 и
и 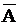 связаны равенством
связаны равенством
+1. 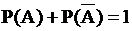 ; 2.
; 2. 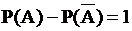 ; 3.
; 3. 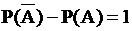 ;
;
4. 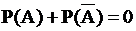 .
.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 40
9.1.2.1
Для произвольных событий 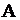 и
и 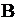 имеет место равенство
имеет место равенство
+1. 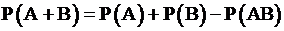 ;
;
2. 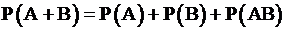 ;
;
3. 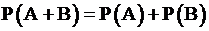 ;
;
4. 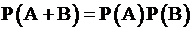 .
.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 41
9.2.1.1
Функция распределения любой случайной величины на всей вещественной оси
+1. не убывает; 2. строго возрастает;
3. строго убывает; 4. постоянна.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 42
9.2.3.1
Значения, принимаемые любой непрерывной случайной величиной,
1. не превосходят 1;
2. образуют конечное множество;
3. положительны;
+4. заполняют некоторый промежуток.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 43
9.2.1.1
Дан закон распределения дискретной случайной величины  :
:
| –1 | 0 | 1 | 2 |
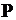
| 0,2 | 0,4 | 0,1 | 0,3 |
Вероятность 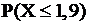 равна
равна
+1. 0,7; 2. 0,1; 3. 0,3. 4. 1.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 44
9.2.1.1
Дан закон распределения дискретной случайной величины 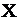 :
:
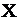
| 0 | 1 | 2 |
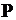
| 0,2 | 0,5 | 0,3 |
Закон распределения случайной величины 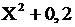 имеет вид:
имеет вид:
| 1. | 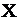
| 0,2 | 1,2 | 2,2 |
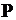
| 0,2 | 0,5 | 0,3 |
| +2. | 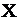
| 0,2 | 1,2 | 4,2 |
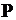
| 0,2 | 0,5 | 0,3 |
| 3. | 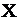
| 0,5 | 1,5 | 4,5 |
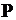
| 0,24 | 0,45 | 0,29 |
| 4. | 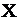
| 0,2 | 1,2 | 4,2 |
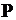
| 0,54 | 0,75 | 0,59 |
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 45
9.2.1.1
Среди приведённых ниже распределений к дискретной случайной величине относится
+1. пуассоновское; 2. нормальное; 3. равномерное; +4. биномиальное.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 46
9.2.1.1
Плотностью вероятности 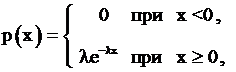 (
(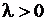 ) задаётся случайная величина, распределённая по
) задаётся случайная величина, распределённая по
+1. показательному закону;
2. нормальному закону;
3. пуассоновскому закону;
+4. экспоненциальному закону.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 47
9.2.1.5
Математическое ожидание произвольной случайной величины
1. положительно;
2. неотрицательно;
+3. может быть любым действительным числом;
4. является целым числом.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 48
9.2.1.6
Дисперсия любой случайной величины
1. меньше 1;
2. не превосходит 1;
3. принадлежит промежутку 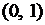 ;
;
+4. неотрицательна.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 49
9.2.3.4
Если функция распределения случайной величины 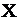 имеет вид
имеет вид
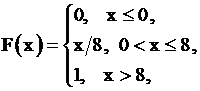
то математическое ожидание 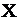 равно
равно
+1. 4; 2.0; 3. 1; 4. 8.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 50
9.2.3.5
Дана плотность распределения вероятностей 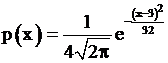 случайной величины
случайной величины 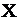 . Математическое ожидание и дисперсия
. Математическое ожидание и дисперсия 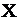 соответственно равны:
соответственно равны:
1. 3 и 4; +2. 3 и 16; 3. 4 и 3; 4. 32 и 3.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 51
9.2.3.5
Случайная величина X распределена по нормальному закону, причём 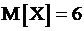 и
и 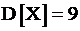 . Плотность распределения вероятностей Х имеет вид:
. Плотность распределения вероятностей Х имеет вид:
1. 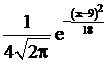 ; 2.
; 2. 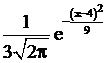 ; 3.
; 3. 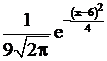 ; +4.
; +4. 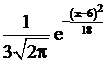 .
.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 52
9.2.3.5
Степень зависимости между двумя случайными величинами оценивается
1. абсолютной величиной разности их дисперсий;
2. абсолютной величиной разности их математических ожиданий;
3. произведением их средних квадратичных отклонений;
+4. коэффициентом корреляции;
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 53
9.1.2.4
Бросаются два игральных кубика. Пусть случайная величина 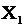 есть число очков, выпавших на первом кубике, а случайная величина
есть число очков, выпавших на первом кубике, а случайная величина 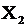 – на втором. Ряд распределения случайной величины
– на втором. Ряд распределения случайной величины 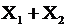 имеет вид:
имеет вид:
| 1. | 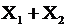
| 1 | 2 | 3 | 4 | 5 | 6 |
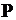
| 0,1 | 0,1 | 0,3 | 0,3 | 0,1 | 0,1 |
| 2. | 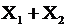
| 1 | 2 | 3 | 4 | 5 |
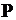
| 0,4 | 0,1 | 0,2 | 0,2 | 0,1 |
| +3. | 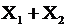
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
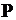
| 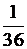
| 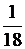
| 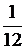
| 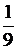
| 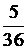
| 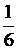
| 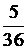
| 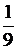
| 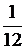
| 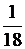
| 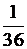
|
| 4. | 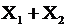
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
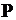
| 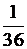
| 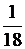
| 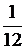
| 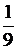
| 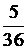
| 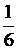
| 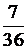
| 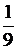
| 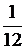
| 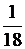
| 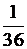
|
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 54
9.2.3.5
В цепи Маркова с дискретным временем шагами называются
1. длительности нахождения системы в её состояниях;
2. длительности промежутков времени между моментами перехода системы
из одного состояния в другое;
3. вероятности нахождения системы в её состояниях;
+4. моменты времени, в которые система может перейти из одного
состояния в другое.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 55
9.2.3.5
Если 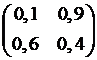 – матрица перехода однородной цепи Маркова
– матрица перехода однородной цепи Маркова
с дискретным временем за один шаг, то матрица перехода за два шага равна
1. 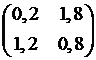 ; 2.
; 2. 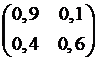 ; 3.
; 3. 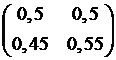 ; +4.
; +4. 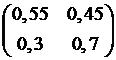 .
.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 56
10.1.2.3
Доверительным называется интервал, который накрывает оцениваемый параметр распределения
1. с вероятностью, равной 1;
2. с вероятностью, равной 0,999;
+3. с некоторой заданной вероятностью;
4. с вероятностью, большей 0,5.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 57
10.1.1.1
Если случайно отобранные из генеральной совокупности объекты
не возвращается обратно, то получаемая выборка называется
1. повторной; 2. репрезентативной;
+3. бесповторной; 4. корреляционной.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 58
10.1.1.1
Пусть 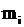 – частотывариант
– частотывариант 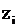 выборки объёма
выборки объёма 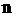 (
(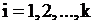 ).
).
Накопленными относительными частотами называются числа
+1. 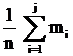 ; +2.
; +2. 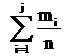 ; 3.
; 3. 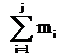 ; 4.
; 4. 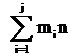 (
(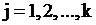 ).
).
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 59
9.2.3.4
Если функция распределения случайной величины X имеет вид
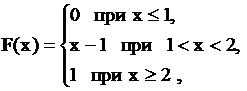
то вероятность 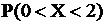 равна
равна
1. 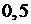 ; 2. 0; +3. 1; 4. 0,99.
; 2. 0; +3. 1; 4. 0,99.
УС: 3
ВРЕМЯ 2 мин.
Т Е С Т № 60
10.1.1.4
 2018-02-14
2018-02-14 226
226






