2018-02-14
243
Оценка параметров парной регрессии выполняется из следующих предпосылок. Наличие случайных отклонений, вызванных воздействием на переменную Y множества других, неучтённых в уравнении факторов, приведёт к тому, что связь наблюдаемых величин xi и yi приобретёт вид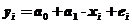 
, где ei – случайные ошибки (отклонения, возмущения). Значения случайных отклонений неизвестны и по наблюдениям xi и yi получаем значения а0 и а1, являющиеся случайными. Надёжность оценок коэффициентов регрессии устанавливается по отклонению переменной Y от оценённой линии регрессии: 
.
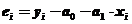Дисперсия ошибки параметра а1 будет равна 
.
Дисперсия ошибки параметра а0 будет равна 
,
где 
(Дисперсия (от лат. dispersio — рассеяние), в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. В статистическом понимании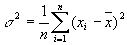 
есть среднее арифметическое из квадратов отклонений величин xi от их среднего арифметического
)
Для оценки статистической значимости коэффициентов регрессии и коэффициента корреляции рассчитывается t-критерий Стьюдента. Выдвигается гипотеза H0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Насколько малой должна быть вероятность для выбора гипотез? В большинстве работ по экономике за критический уровень берётся уровень 5% или 1%.
Оценка значимости коэффициентов регрессии и корреляции с помощью t –критерия Стьюдента проводится путём сопоставления их значений с величиной случайной ошибки. Наблюдаемые значения t-критерия рассчитываются по формулам:
где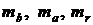 
– случайные ошибки параметров линейной регрессии и коэффициента корреляции.
Случайные ошибки рассчитываются по формулам:
Что такое
Где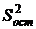 
– остаточная дисперсия на одну степень свободы, 
Табличное (критическое) значение t-статистики находят по таблицам распределения t-Стьюдента при выбранном уровне значимости и числе степеней свободы 
. Сравнивая фактическое и критическое (табличное) значения t-статистики, принимаем или отвергаем гипотезу Н0. Если tтабл < tфакт, то H0 отклоняется, т.е. коэффициенты регрессии не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора.
Связь между F- критерием Фишера и t –статистикой Стьюдента выражается равенством
.
Доверительный интервал определяет пределы значений парасметров регрессии с учётом ошибок выборки, в которых в соответствии с выбранной вероятностью находится этот параметр. Другими словами, для (1-р) • 100% выборок истинное значение параметра будет лежать в данном доверительном интервале.
Для расчёта доверительного интервала определяем предельную ошибку D для каждого показателя. 
Формулы для расчёта доверительных интервалов имеют следующий вид:
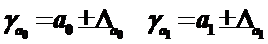
Если в границы доверительного интервала попадает 0, т.е. нижняя граница отрицательная, а верхняя – положительная, то оцениваемый параметр принимается нулевым, что равносильно незначимости этого коэффициента, и поэтому его экономическая интерпретация не имеет смысла.
На основании построенной модели можно найти прогнозные значения зависимой переменной Y, которые отвечают ожидаемому значению независимой переменной X. Прогнозное значение Yp определяется путём подстановки в уравнение регрессии соответствующего (прогнозного) значения Xp. Вычисляется средняя ошибка прогноза 
И строится доверительный интервал прогноза:
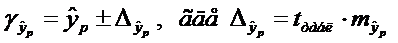
С надежностью 0,95 прогнозное значение y заключено в данном доверительном интервале, и если, границы не принимают нулевых значений можно сделать вывод о статистической надежности прогноза.
