Эконометрика
Учебное пособие.
Арзамас 2008
УДК 330 (075.8)
ББК 65.01 я 73
С 78
Печатается по решению редакционно-издательского совета ГОУ ВПО «Арзамасский государственный педагогический институт им. А.П. Гайдара»
Рецензенты: Рецензенты: д.т.н., профессор Арзамасского политехнического института Н.П. Ямпурин,
заведующий кафедрой математического анализа Арзамасского государственного педагогического института, к.физ-мат. наук, доцент Л.В. Широков
Статуев А.А.
C 78 Эконометрика. Учебное пособие. – Арзамас: АГПИ, 2008. – 128 с.
В данном пособии в сжатом виде излагаются основные теоретические сведения, даются основные понятия, модели и методы эконометрики, приведены примеры решения задач.
Учебне пособие предназначено для студентов, обучающихся по направлению «прикладная информатика». Материалы, содержащиеся в данном пособии, могут быть использованы в преподавании одноимённой дисциплины учебного плана по другим специальностям.
УДК 330(075.8)
ББК 65.01 я 73
©Статуев А.А., 2008.
©Арзамасский государственный педагогический институт им. А.П. Гайдара, 2008.
Содержание
Введение…………………………………………………………………………..4
1. Элементы теории вероятностей и математической статистики…………….5
2. Эконометрика и эконометрическое моделирование………………………..11
3. Парная регрессия и корреляция……………………………………………...17
3.1 Линейная модель парной регрессии и корреляции…………………21
3.2 Нелинейные модели парной регрессии и корреляции……………...28
4. Множественная регрессия и корреляция……………………………………39
4.1 Спецификация модели………………………………………………..39
4.2 Метод наименьших квадратов (МНК)………………………………43
4.3 Линейные регрессионные модели с гетероскедастичными
остатками……………………………………………………………...60
4.4 Обобщенный метод наименьших квадратов (ОМНК)……………...65
4.5 Регрессионные модели с переменной структурой (фиктивные переменные)…………………………………………………………...71
5. Временные ряды………………………………………………………………82
5.1 Автокорреляция уровней временного ряда…………………………83
5.2 Моделирование тенденции временного ряда……………………….88
5.3 Моделирование сезонных колебаний………………………………..89
5.4 Автокорреляция в остатках. Критерий Дарбина-Уотсона…………97
6. Системы эконометрических уравнений……………………………………100
6.1 Структурная и приведенная формы модели……………………….101
6.2 Проблема идентификации…………………………………………..104
6.3 Методы оценки параметров структурной формы модели………...108
Приложение 1. Примеры решения типовых задач…………………………...111
Приложение 2. Тестовые задания……………………………………………..114
Приложение 3. Вопросы к экзамену…………………………………………..122
Приложение 4. Математико-статистические таблицы……………………....123
Литература……………………………………………………………………...126
Введение
В последнее время специалисты, обладающие знаниями и навыками проведения прикладного экономического анализа с использованием доступных математических и программных средств, пользуются спросом на рынке труда. Одной из центральных дисциплин в подготовке таких специалистов является дисциплина "Эконометрика".
Эконометрика является областью знаний, которая охватывает вопросы применения статистических методов к теоретическим моделям, описывающим реальные экономические процессы.
Очевидно, что с помощью моделей можно получить много информации об экономических процессах, объяснить те или иные явления или процессы, но никогда не удастся получить всю информацию и однозначно определить истинный механизм экономического процесса или явления.
И даже в тех случаях, когда достаточно адекватная исходным данным эконометрическая модель построена и вопрос только в использовании ее для объяснения экономической ситуации или принятия решения, следует весьма осторожно подходить к выводам и рекомендациям, следующим из модельных оценок.
Эконометрический анализ, как правило, проводят с помощью ПЭВМ. В последние несколько лет сформировался обширный набор из пакетов прикладных программ, позволяющих автоматизировать процессы такого анализа. К наиболее распространенным относятся пакеты SAS, SPSS, Stata, Eviews и др. Имеются простейшие опции для проведения эконометрического анализа в Excel.
В настоящем пособии даются основные понятия, модели и методы эконометрики, рассматриваются примеры решения задач.
Для работы с предлагаемым изданием необходимы базовые знания некоторых разделов следующих учебных дисциплин: высшая математика, теория вероятностей, математическая статистика, общая теория статистики.
1. Элементы теории вероятностей и математической статистики
Согласно классическому определению вероятность события А равна отношению числа случаев т, благоприятствующих ему, к общему числу случаев n, т.е. Р(А)=т/п.
Одним из важнейших понятий теории вероятностей является понятие случайной величины.
Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — заранее не известно).
Для дискретной случайной величины множество возможных значений случайной величины, т.е. функции f(x), конечно или счетно, для непрерывной — бесконечно и несчетно.
Примеры случайных величин:
X — число родившихся детей в течение суток в г. Москве;
У— число произведенных выстрелов до первого попадания;
Z— дальность полета артиллерийского снаряда.
Здесь X, У — дискретные случайные величины, a Z — непрерывная случайная величина.
Наиболее полным, исчерпывающим описанием случайной величины является ее закон распределения.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.
Например,
| X | x1 | x2 | … | xi | … | xn |
| p1 | p2 | … | pi | … | pn |
Такая таблица называется рядом распределения дискретной случайной величины.
Для любой дискретной случайной величины

Если по оси абсцисс откладывать значения случайной величины, по оси ординат — соответствующие их вероятности, то получаемая (соединением точек) ломаная называется многоугольником или полигоном распределения вероятностей.
Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина.
Закон (ряд) распределения дискретной случайной величины дает исчерпывающую информацию о ней, так как позволяет вычислить вероятности любых событий, связанных со случайной величиной. Однако такой закон (ряд) распределения бывает трудно обозримым и не всегда удобным для анализа
Поэтому для описания случайных величин часто используются их числовые характеристики — числа, в сжатой форме выражающие наиболее существенные черты распределения случайной величины. Наиболее важными из них являются математическое ожидание, дисперсия, среднее квадратичное отклонение и др. Числовые характеристики случайных величин являются числами неслучайными, определенными.
Математическим ожиданием, или средним значением, М(Х) дискретной случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:

Свойства математического ожидания:
1) М(С) = С где С - постоянная величина;
2) М(кХ) = кМ(Х);
3) М(Х± У) = М(Х)± М(У)
4) М(ХУ) = М(Х) • М(У), где X, Y — независимые случайные величины;
5) М(Х± С) = М(Х)± С;
Дисперсией D(X) случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания:
D(X) = M[X-M(X)]2
или D{X) = M(X-a)2, где а = М(Х).
Дисперсия характеризует отклонение (разброс, рассеяние, вариацию) значений случайной величины относительно среднего значения. Если случайная величина X — дискретная с конечным числом значений, то:

Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
 ,
,
которая называется средним квадратичным отклонением (стандартным отклонением или стандартом) случайной величины X.
Функцией распределения случайной величины X называется функция F(x), выражающая для каждого х вероятность того, что случайная величина X примет значение, меньшее х:
F(x) = P(X<x).
Свойства функции распределения:
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: 0 < F(x) < 1.
2.Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. при х2 > х1 F(x2) > F(x1).
3.На минус бесконечности функция распределения равна нулю, на плюс бесконечности — равна единице, т.е.

4. Вероятность попадания случайной величины X в интервал [х1,х2) (включая x1) равна приращению ее функции распределения на этом интервале, т.е.
P(x1<x<x2) = F(x2)-F{xl)
Случайная величина X называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
Для непрерывной случайной величины X вероятность любого отдельно взятого значения равна нулю, т.е. P(x=x1)=0, а вероятность попадания X в интервал (х1, х2) не зависит от того, является ли этот интервал открытым или закрытым, т.е., например, 
Плотностью вероятности (плотностью распределения) непрерывной случайной величины X называется производная ее функции распределения

Плотность вероятности  ,как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин.
,как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин.
График плотности вероятности называется кривой распределения.
Свойства плотности вероятности непрерывной случайной величины:
1.Плотность вероятности — неотрицательная функция, т.е.  .
.
2. Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от а до b(рис. 1.1),

Рис. 1.1. Вероятность попадания случайной величины в интервал [а,b].
т.е. 

Рис. 1.2. Функция распределения случайной величины
3. Функция распределения непрерывной случайной величины (рис. 1.2) может быть выражена через плотность вероятности по формуле:

4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:

Геометрически свойства 1 - 4 плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
Для непрерывной случайной величины X математическое ожидание М(Х) и дисперсия D(X) определяются по формулам:
 , если интеграл абсолютно сходится;
, если интеграл абсолютно сходится;
Наряду с отмеченными выше числовыми характеристиками для описания случайной величины используется понятие квантилей и процентных точек.
Квантилем уровня q (или q-квантилем) называется такое значение xq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
F(xq)=P(X<xq)=q
(100q)%-ой точкой называется квантиль X1-q.
Упорядоченный набор Х=(Х1, Х2,..., Хn) случайных величин называется многомерной (n -мерной) случайной величиной (или системой случайных величин, n -мерным вектором).
Функцией распределения n -мерной случайной величины (Х1, Х2,..., Хn) называется функция F(х1,х2,...,хп), выражающая вероятность совместного выполнения n неравенств Х1 <x1, X2 <x2,...,Xn <xn т.е.
F(x1,x2,...,xn)=P(Х1 <x1, X2 <x2,...,Xn <xn)
В двумерном случае для случайной величины (X, Y) функция распределения F(x, у) определится равенством: F(x,y)=P(X<x, Y<y).
Все свойства и понятия, приводимые далее для двумерной случайной величины могут быть перенесены на случай n >2. Свойства функции распределения F(x,y) аналогичны свойствам одномерной случайной величины.
Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины (X, Y) называется вторая смешанная частная производная ее функции распределения, т.е.
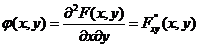
Свойства плотности вероятности двумерной случайной величиныаналогичны свойствам плотности вероятности одномерной случайной величины:
Условным законом распределения одной из одномерных составляющих двумерной случайной величины (X, Y) называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в какой-то интервал).
Числовые характеристики условных распределений: условные математические ожидания Mx(Y) и Мy(Х) и условные дисперсии Dx(Y) и Dy(X). Эти характеристики находятся по обычным формулам математического ожидания и дисперсии, в которых вместо вероятностей событий или плотностей вероятности используются условные вероятности или условные плотности вероятности.
Условное математическое ожидание случайной величины Y при Х=х, т. е. Mx(Y), есть функция от х, называемая функцией регрессии или просто регрессией Y по X; аналогично Мy(Х) называется функцией регрессии или просто регрессией X по У. Графики этих функций называются соответственно линиями регрессии (или кривыми регрессии) Y по X и X по У.
Зависимость между двумя случайными величинами называется вероятностной (стохастической или статистической), если каждому значению одной из них соответствует определенное (условное) распределение другой.
Ковариацией (или корреляционным моментом) Соv(Х,У) случайных величин X и У называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е. Соv(Х,У)=M[(X-ax)(Y-ay)], где ах = M(X), ay = M(Y).
Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки (ах, ау). Ковариация — величина размерная, что затрудняет ее использование для оценки степени зависимости случайных величин. Этих недостатков лишен коэффициент корреляции.
Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратичных отклонений этих величин:
 .
.
Из определения следует, что коэффициент корреляции — величина безразмерная, характеризующая тесноту линейной зависимости между случайными величинами.
2. Эконометрика и эконометрическое моделирование
Термин эконометрика был введен в научную литературу в 1930 году норвежским статистиком Рагнаром Фришем для обозначения нового направления научных исследований, возникшего из необходимости научно-обоснованного подтверждения и доказательства концепций и выводов экономической теории результатами количественного анализа рассматриваемых процессов. В этой связи можно сказать, что основная задача эконометрики состоит в построении эконометрических моделей, описывающих взаимообусловленное развитие социально-экономических процессов, на основе информации, отражающей распределение их уровней во времени или (и) в пространстве однородных объектов. Эти модели используются в анализе и прогнозировании общих закономерностей и конкретных количественных характеристик рассматриваемых процессов, определении управляющих воздействий.
Основной целью эконометрики является модельное описание конкретных количественных взаимосвязей, обусловленных общими качественными закономерностями, изученными в экономической теории.
Эконометрика - относительно молодая научная дисциплина, сформировавшаяся во второй половине XX века и развивающаяся на стыке экономической теории (макроэкономика, микроэкономика, математическая экономика), социально-экономической статистики (включая информационное обеспечение экономических исследований) и теории вероятностей и математической статистики.
Основными методами эконометрики являются регрессионный анализ, анализ временных рядов, системы одновременных уравнений, статистические методы классификации и снижения размерности.
Эконометрика – это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе экономической теории, экономической статистики и экономических измерений, математико-статистического инструментария придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией.
Эконометрика не только выявляет объективно существующие экономические законы и связи между экономическими показателями, качественно определенными в экономической теории, но и формирует подходы к их формализации и количественному выражению.
В рамках экономического анализа, как правило, выдвигаются какие-либо гипотезы, строятся теории, объясняющие явление или процесс. Узкое место заключается в подтверждении теоретических гипотез фактическими данными. Поэтому в количественном экономическом анализе главную роль играет формирование гипотезы и ее проверка. Интуитивные утверждения должны приобрести форму предположений, которые могут быть либо приняты, либо отвергнуты после сопоставления с наблюдаемыми фактами.
Вопросами применения статистических методов к теоретическим моделям, описывающим реальные хозяйственные процессы, и занимается эконометрика. Экономическая статистика как элемент информационного обеспечения эконометрики предполагает решение таких задач, как выбор необходимых статистических показателей и обоснование способа их измерения, определение плана статистического обследования и т.д.
Под математико-статистическим инструментарием в эконометрике подразумеваются отдельные расширенные разделы математической статистики, связанные с регрессионным анализом (классическая модель регрессии и классический метод наименьших квадратов, обобщенная модель регрессии и обобщенный метод наименьших квадратов), построением и анализом моделей временных рядов и систем одновременных уравнений.
Вместе с тем, необходимо различать эконометрику и математическую экономику. Именно приземление экономической теории на базу конкретной экономической статистики и извлечение из этого приземления с помощью подходящего математического аппарата вполне определенных количественных взаимосвязей являются ключевыми моментами в понимании сущности эконометрики, разграничении её с математической экономикой, описательной экономической статистикой и математической статистикой.
Так, математическая экономика - это математически сформулированная экономическая теория, которая изучает взаимосвязи между экономическими переменными на абстрактном (неколичественном) уровне. Она становится эконометрикой, когда символически представленные в этих взаимосвязях коэффициенты заменяются конкретными численными оценками, полученными на базе соответствующих экономических данных.
Области применения эконометрических моделей напрямую связаны с целями эконометрического моделирования, основными из которых являются:
1) прогноз экономических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы;
2) имитация различных возможных сценариев социально-экономического развития анализируемой системы.
В любой эконометрической модели, в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на:
- экзогенные переменные, задаваемые как бы извне, автономно, в определен ной степени управляемые (планируемые);
- эндогенные переменные, значения которых формируются в процессе и внутри функционирования анализируемой социально-экономической системы под воздействием экзогенных переменных и во взаимодействии друг с другом, являются предметом объяснения в эконометрической модели;
- предопределенные переменные выступают в роли факторов-аргументов или объясняющих переменных;
- лаговые эндогенные переменные входят в уравнения анализируемой эконометрической системы, но измерены в прошлые моменты, а следовательно, являются уже известными, заданными.
Эконометрическая модель служит для объяснения поведения эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных.
Эконометрический метод складывался в преодолении следующих трудностей, искажающих результаты применения классических статистических методов (сущность новых терминов будет раскрыта в дальнейшем):
1. асимметричности связей;
2. мультиколлинеарности связей;
3. эффекта гетероскедастичности;
4. автокорреляции;
5. ложной корреляции;
6. наличия лагов.
Весь процесс эконометрического моделирования можно разбить на шесть основных этапов.
1-й этап (постановочный) - определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли;
2-й этап (априорный) - предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез;
3-й этап (параметризация) - собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными;
4-й этап (информационный) - сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей;
5-й этап (идентификация модели) - статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели. Он непосредственно связан с проблемой идентифицируемости модели, то есть необходимо предложить и реализовать математически корректную процедуру оценивания неизвестных параметров модели по имеющимся исходным данным;
6-й этап (верификация модели) - сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных. В ходе верификации модели решаются вопросы о том:
- насколько удачно удалось решить проблемы спецификации, идентифицируемости и идентификации, т.е. можно ли рассчитывать на то, что использование полученной модели в целях прогноза даст результаты, адекватные действительности;
- какова точность (абсолютная, относительная) прогнозных и имитационных расчетов основанных на построенной модели;
Наиболее распространенными в эконометрическом моделировании являются следующие образующие четыре группы методы:
- классическая линейная модель множественной регрессии (КЛММР) и классический метод наименьших квадратов (МНК);
- обобщенная КЛММР и обобщенный МНК;
- методы статистического анализа временных рядов;
- методы анализа систем одновременных эконометрических уравнений.
Применение этих методов делает возможным построение следующих типов эконометрических моделей:
1. Регрессионные модели с одним уравнением.
В таких моделях зависимая (объясняемая) переменная у представляется в виде функции
y = f(x, b) = f(x1,...,xk,b1,...,bk ),
где х1,,х2,...,хk - независимые (объясняющие) переменные, b1,...,bk -параметры.
В зависимости от вида функции f(x,b) модели делятся на линейные и нелинейные.
2. Модели временных рядов.
К этому классу относятся модели:
• тренда: y(t) = Ti(t) + ut, где t - время, T(t) - временной тренд заданного параметрического вида, u - случайная (стохастическая) компонента;
• сезонности: yi(t) = Si(t)+ ut, где Si(t) - периодическая (сезонная) компонента, ut - случайная (стохастическая) компонента.
• тренда и сезонности: уi(t) = Ti(t) + Si(t) + ut (аддитивная) или уi(t) = Ti(t)Si(t)+ut, (мультипликативная), где T(t) - временной тренд заданного параметрического вида, Si(t) - периодическая (сезонная) компонента, ut - случайная (стохастическая) компонента.
Кроме того, существуют модели временных рядов, в которых присутствует циклическая компонента, формирующая изменения анализируемого признака, обусловленные действием долговременных циклов экономической, демографической или астрофизической природы (волны Кондратьева, циклы солнечной активности и т.д.).
Модели временных рядов могут применяться для изучения и прогнозирования объема продаж туристических путевок, спроса на железнодорожные и авиабилеты, при краткосрочном прогнозировании процентных ставок и т.д.
3. Системы одновременных уравнений.
Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых, кроме объясняющих переменных, может включать в себя объясняемые переменные из других уравнений системы. Системы одновременных уравнений требуют сложного математического аппарата и могут быть использованы для моделей национальной экономики. Ярким примером системы одновременных уравнений служит модель спроса и предложения.
Для эконометрического моделирования используются данные следующих трех типов.
1. Предположим, что мы располагаем результатами регистрации значений переменных (х1, х2,..., хр) на n статистически обследованных объектах. Так что если i - номер обследованного объекта, то имеющиеся исходные статистические данные состоят из n строк вида (хi1, хi2,..., хi p), где xi j - значение j переменной, зарегистрированное на i обследованном объекте. То есть данные могут быть представлены в виде матрицы п х р:

Такой тип данных называется пространственной выборкой или данными поперечного среза (cross-section data). Такие данные не имеют временного параметра, и порядок их следования не существенен. Пример: финансовые показатели работы предприятий за истекший год.
2. Предположим, что данные регистрируются на одном и том же объекте, но в разные периоды времени. Тогда аналогом i будет номер периода времени, к которому привязаны соответствующие данные, а п будет общим числом периодов времени. Такие данные называются временной выборкой, или временными рядами данных (time series data), или данными продольного среза. Идя таких данных существенен порядок следования значений переменных. Пример: финансовые показатели предприятия за последние несколько лет.
3. Наконец, предположим, что отслеживается каждый из п объектов в течение Т периодов времени. То есть имеем последовательность матриц вида X, отнесенных к моментам времени 1,2,...,Т:

Такие данные называются панельными, или пространственно-временной выборкой (panel data). Данные сочетают в себе свойства как временных рядов, так и данных поперечного сечения. Как правило, значение Т мало. Пример: показатели социально-экономического состояния домохозяйств за три года.
3. Парная регрессия и корреляция
Рассмотрим некоторый экономический объект (процесс, явление, систему) и выделим только две переменные, характеризующие объект. Обозначим переменные буквами Y и X. Будем предполагать, что независимая (объясняющая) переменная X оказывает воздействие на значения переменной Y, которая, таким образом, является зависимой переменной, т.е. имеет место зависимость: Y=f(X). (3.1)
Зависимость (3.1) можно рассматривать с целью установления самого факта наличия или отсутствия значимой связи между Y и X, можно преследовать цель прогнозирования неизвестных значений Y по известным значениям X, наконец возможно выявление причинно-следственных связей между X и Y.
При изучении взаимосвязи между переменными Y и X следует, прежде всего, установить тип зависимости (природу анализируемых переменных Y и X). Возможны следующие ситуации:
· Y и Х являются неслучайными переменными, т.е. значения Y строго зависят только от соответствующих значений X и полностью ими определяются. В этом случае говорят о функциональной зависимости, когда Y является некоторой функцией от переменной X и верна модель (3.1).
· Y является случайной переменной, а X - неслучайной. В этом случае считают, что между переменными имеет место регрессионная зависимость. То есть верна модель  , где
, где  - величина случайной ошибки.
- величина случайной ошибки.
· Y и X зависят от множества неконтролируемых факторов, так что являются случайными по своей сущности. В этом случае к проблемам построения конкретного вида зависимости между указанными переменными присоединяется проблема исследования тесноты связи между этими переменными. Речь в этом случае идет о корреляционно-регрессионной зависимости между Y и X.
Будем предполагать наличие второй из указанных ситуаций. Регрессионный анализ является инструментом решения следующих основных задач:
1.Для любых значений объясняющей переменной X построить наилучшие по некоторому критерию оценки для неизвестной функции f(X).
2.По заданным значениям объясняющей переменной X построить наилучший по некоторому критерию прогноз для неизвестного значения результирующей переменной Y(X).
3.Пусть известно, что искомая функция зависит от параметра b f(X, b). Требуется построить наилучшую в определенном смысле оценку для неизвестного значения этого параметра.
4.Оценить удельный вес влияния переменной X на результирующий показатель Y.
Парная регрессия представляет собой регрессию между двумя переменными –  и
и  , т. е. модель вида:
, т. е. модель вида:
 ,
,
где  – зависимая переменная (результативный признак);
– зависимая переменная (результативный признак);  – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными
– независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными  и
и  нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина
нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина  складывается из двух слагаемых:
складывается из двух слагаемых:
 ,
,
где  – фактическое значение результативного признака;
– фактическое значение результативного признака;  – теоретическое значение результативного признака, найденное исходя из уравнения регрессии;
– теоретическое значение результативного признака, найденное исходя из уравнения регрессии;  – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина  называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака  , подходят к фактическим данным
, подходят к фактическим данным  .
.
К ошибкам спецификации относятся неправильный выбор той или иной математической функции для  и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
Наряду с ошибками спецификации могут иметь место ошибки выборки, которые имеют место в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.
Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии.
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.
Особенно велика роль ошибок измерения при исследовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем, статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например, в результате наличия скрытых доходов.
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.
В парной регрессии выбор вида математической функции  может быть осуществлен тремя методами:
может быть осуществлен тремя методами:
1) графическим;
2) аналитическим, т.е. исходя из теории изучаемой взаимосвязи;
3) экспериментальным.
При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рис. 3.1:
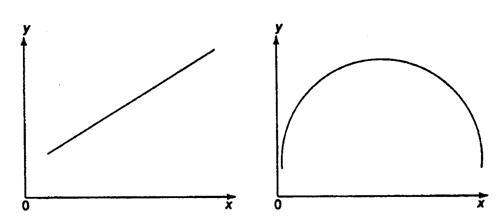








Рис. 3.1. Основные типы кривых, используемые при количественной оценке связей между двумя переменными.
Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.
При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии  , рассчитанной при разных моделях.
, рассчитанной при разных моделях.
Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии  , то фактические значения результативного признака совпадают с теоретическими
, то фактические значения результативного признака совпадают с теоретическими  , т.е. они полностью обусловлены влиянием фактора
, т.е. они полностью обусловлены влиянием фактора  . В этом случае остаточная дисперсия
. В этом случае остаточная дисперсия 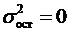 .
.
В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии, факторов. Иными словами, имеют место отклонения фактических данных от теоретических  . Величина этих отклонений и лежит в основе расчета остаточной дисперсии:
. Величина этих отклонений и лежит в основе расчета остаточной дисперсии:
 .
.
Чем меньше величина остаточной дисперсии, тем меньше влияние не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным.
Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной  . Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при
. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при  должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени
должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени  , то требуется объем информации уже не менее 14 наблюдений.
, то требуется объем информации уже не менее 14 наблюдений.
3.1 Линейная модель парной регрессии и корреляции
Рассмотрим простейшую модель парной регрессии – линейную регрессию. Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
 или
или  . (3.2)
. (3.2)
Уравнение вида  позволяет по заданным значениям фактора
позволяет по заданным значениям фактора  находить теоретические значения результативного признака, подставляя в него фактические значения фактора
находить теоретические значения результативного признака, подставляя в него фактические значения фактора  .
.
Построение линейной регрессии сводится к оценке ее параметров – 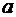 и
и  . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров
. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 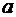 и
и  , при которых сумма квадратов отклонений фактических значений результативного признака
, при которых сумма квадратов отклонений фактических значений результативного признака  от теоретических
от теоретических  минимальна:
минимальна:
 . (3.3)
. (3.3)
Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 3.2):

Рис. 3.2. Линия регрессии с минимальной дисперсией остатков.
Как известно из курса математического анализа, чтобы найти минимум функции (3.2), надо вычислить частные производные по каждому из параметров 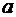 и
и  и приравнять их к нулю. Обозначим
и приравнять их к нулю. Обозначим  через
через  , тогда:
, тогда:
 .
.
 (3.4)
(3.4)
После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров 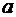 и
и  :
:
 (3.5)
(3.5)
Решая систему уравнений (3.5), найдем искомые оценки параметров 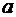 и
и  . Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (3.5):
. Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (3.5):
 ,
,  , (3.6)
, (3.6)
где  – ковариация признаков
– ковариация признаков  и
и  ,
, 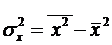 – дисперсия признака
– дисперсия признака  .
.
 ,
,  ,
, 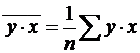 ,
,  .
.
Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.
Параметр  называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
Формально 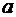 – значение
– значение  при
при  . Если признак-фактор
. Если признак-фактор  не может иметь нулевого значения, то вышеуказанная трактовка свободного члена
не может иметь нулевого значения, то вышеуказанная трактовка свободного члена 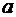 не имеет смысла, т.е. параметр
не имеет смысла, т.е. параметр 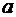 может не иметь экономического содержания.
может не иметь экономического содержания.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции  , который можно рассчитать по следующим формулам:
, который можно рассчитать по следующим формулам:
 . (3.7)
. (3.7)
Линейный коэффициент корреляции находится в пределах:  . Чем ближе абсолютное значение
. Чем ближе абсолютное значение  к единице, тем сильнее линейная связь между факторами (при
к единице, тем сильнее линейная связь между факторами (при  имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.
имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции  , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака
, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака  , объясняемую регрессией, в общей дисперсии результативного признака:
, объясняемую регрессией, в общей дисперсии результативного признака:
 , (3.8)
, (3.8)
где  ,
,  .
.
Соответственно величина  характеризует долю дисперсии
характеризует долю дисперсии  , вызванную влиянием остальных, не учтенных в модели, факторов.
, вызванную влиянием остальных, не учтенных в модели, факторов.
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:
 . (3.9)
. (3.9)
Средняя ошибка аппроксимации не должна превышать 8–10%.
Оценка значимости уравнения регрессии в целом производится на основе  -критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.
-критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.
Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной  от среднего значения
от среднего значения  раскладывается на две части – «объясненную» и «необъясненную»:
раскладывается на две части – «объясненную» и «необъясненную»:
 ,
,
где  – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;  – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);  – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.
– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.
Схема дисперсионного анализа имеет вид, представленный в таблице 1.1 ( – число наблюдений,
– число наблюдений,  – число параметров при переменной
– число параметров при переменной  ).
).
Таблица 3.1
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Дисперсия на одну степень свободы |
| Общая | 
| 
| 
|
| Факторная | 
| 
| 
|
| Остаточная | 
| 
| 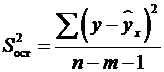
|
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину  -критерия Фишера:
-критерия Фишера:
 . (3.10)
. (3.10)
Фактическое значение  -критерия Фишера (3.10) сравнивается с табличным значением
-критерия Фишера (3.10) сравнивается с табличным значением  при уровне значимости
при уровне значимости  и степенях свободы
и степенях свободы  и
и  . При этом, если фактическое значение
. При этом, если фактическое значение  -критерия больше табличного, то признается статистическая значимость уравнения в целом.
-критерия больше табличного, то признается статистическая значимость уравнения в целом.
Для парной линейной регрессии  , поэтому
, поэтому
 . (3.11)
. (3.11)
Величина  -критерия связана с коэффициентом детерминации
-критерия связана с коэффициентом детерминации  , и ее можно рассчитать по следующей формуле:
, и ее можно рассчитать по следующей формуле:
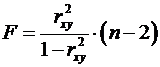 . (3.12)
. (3.12)
В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: 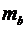 и
и  .
.
Стандартная ошибка коэффициента регрессии определяется по формуле:
 , (3.13)
, (3.13)
где  – остаточная дисперсия на одну степень свободы.
– остаточная дисперсия на одну степень свободы.
Величина стандартной ошибки совместно с  -распределением Стьюдента при
-распределением Стьюдента при  степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.
степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение  -критерия Стьюдента:
-критерия Стьюдента:  которое затем сравнивается с табличным значением при определенном уровне значимости
которое затем сравнивается с табличным значением при определенном уровне значимости  и числе степеней свободы
и числе степеней свободы 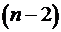 . Доверительный интервал для коэффициента регрессии определяется как
. Доверительный интервал для коэффициента регрессии определяется как  . Поскольку знак коэффициента регрессии указывает на рост результативного признака
. Поскольку знак коэффициента регрессии указывает на рост результативного признака  при увеличении признака-фактора
при увеличении признака-фактора  (
( ), уменьшение результативного признака при увеличении признака-фактора (
), уменьшение результативного признака при увеличении признака-фактора ( ) или его независимость от независимой переменной (
) или его независимость от независимой переменной ( ) (см. рис. 1.3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например,
) (см. рис. 1.3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например,  . Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.

Рис. 3.3. Наклон линии регрессии в зависимости от значения параметра  .
.
Стандартная ошибка параметра 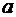 определяется по формуле:
определяется по формуле:
 . (3.14)
. (3.14)
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется  -критерий:
-критерий:  , его величина сравнивается с табличным значением при
, его величина сравнивается с табличным значением при  степенях свободы.
степенях свободы.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции  :
:
 . (3.15)
. (3.15)
Фактическое значение  -критерия Стьюдента определяется как
-критерия Стьюдента определяется как  .
.
Существует связь между  -критерием Стьюдента и
-критерием Стьюдента и  -критерием Фишера:
-критерием Фишера:
 . (3.16)
. (3.16)
В прогнозных расчетах по уравнению регрессии определяется предсказываемое  значение как точечный прогноз
значение как точечный прогноз  при
при  , т.е. путем подстановки в уравнение регрессии
, т.е. путем подстановки в уравнение регрессии  соответствующего значения
соответствующего значения  . Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки
. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки  , т.е.
, т.е.  , и соответственно интервальной оценкой прогнозного значения
, и соответственно интервальной оценкой прогнозного значения  :
:
 ,
,
где 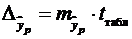 , а
, а  – средняя ошибка прогнозируемого индивидуального значения:
– средняя ошибка прогнозируемого индивидуального значения:
 . (3.17)
. (3.17)
3.2 Нелинейные модели парной регрессии и корреляции
Если между экономическими явлениями суще
 2018-02-14
2018-02-14 690
690






