Анализ тенденции развития (тренда) временного ряда

Севастополь

2011

 

УДК 658

Анализ временных рядовпри помощи системы Мinitab для Windows. Методические указания к выполнению лабораторной работы для студентов всех форм обучения специальности 7.050106 «Учет и аудит»  / Сост. ст. преп. М.В.Потанина, ст.пр. М.В. Погорелова – Севастополь: Изд-во СевНТУ, 2011. – 26 с.

Целью методических указаний является получение навыков студентами в применении  анализа временных рядов при анализе экономических данных,  а также применения анализа временных рядов   для решения сложных экономических задач.

Методические указания утверждены на заседании кафедры менеджмента и экономико-математических методов Севастопольского национального технического университета, протокол №___ от «___» ___________ 2011 г.

Допущено учебно-методическим центром СевНТУ в качестве методических указаний.

Рецензент Букач Б.А., к.э.н, доцент кафедры Менеджмента и экономико-математических методов

 

Содержание

Цель Работы.. 4

1. Теоретические сведения.. 4

1.1 Анализ тенденции развития (тренда) временного ряда 4

1.2 Декомпозиция временного ряда. Анализ сезонных колебаний 5

2. Анализ ВРЕМЕННЫХ РЯДОВ с помощью системы MINITAB.. 11

3. Задание по выполнению лабораторной работы.. 23

4. Порядок выполнения работы.. 25

5. Контрольные вопросы.. 25

6. Библиографический список.. 26

 

Цель Работы

 

Изучение и получение практических навыков в использовании анализа временных рядов, выявлении тенденции их развития (тренда), сезонных колебаний,  прогноз динамики развития временных рядов  при обработке экономической информации с помощью статистического пакета MINITAB For Windows

Теоретические сведения

 

Анализ тенденции развития (тренда) временного ряда

 

На практике экономист весьма часто сталкивается с тем, что исходные данные, которыми он распола­гает для выявления той или иной закономерности, представлены в виде временных (динамических) рядов. Такие ряды описывают изменение некоторой характеристики во времени. Каждый член (уровень) такого ряда связан с соответствующим моментом вре­мени или временным интервалом. Разумеется, уровни ряда долж­ны быть сопоставимыми по своему содержанию. Показатели вре­менных рядов формируются под совокупным влиянием множества длительно и кратковременно действующих факторов и, в том числе, различного рода случайностей. Изменение условий развития явле­ния приводит к более или менее интенсивной смене самих фак­торов, к изменению силы и результативности их воздействия и, в конечном счете, к вариации уровня изучаемого явления во вре­мени. Лишь в очень редких случаях в экономике встречаются чисто стационарные ряды, т. е. ряды, в которых не наблюдаются систематические изменения в средних значениях уровней, их дис­персиях, и эти характеристики не зависят от начала отсчета вре­мени. В таких случаях вариацию уровней можно изучать с по­мощью специального раздела математической статистики — теории стационарных процессов. В основном временные ряды, с которыми имеют дело в экономике, не являются стационарными. Последо­вательность расположения исследуемых данных во времени в та­ких рядах имеет существенное значение для анализа, т. е. время здесь выступает как один из определяющих для изучаемого явле­ния факторов.

Можно выделить три основные задачи исследования временных рядов.

Первая из них заключает­ся в описании изменения соответствующего показателя во вре­мени и выявлении тех или иных свойств исследуемого ряда. Для этого прибегают к разнообразным способам: расчету обобщающего показателя изменения уровней во времени — среднего темпа роста; применению различных сглаживающих фильтров, умень­шающих колебания уровней во времени и позволяющих более чет­ко представить тенденции развития; подбору кривых, характери­зующих эту тенденцию; выделению сезонных и иных периодиче­ских и случайных колебаний; измерению зависимости между чле­нами ряда (автокорреляции). К методам описания какого-либо свойства динамики можно с некоторым основанием отнести и ме­тоды проверки наличия или отсутствия долговременных тенденций в ряду.

Второй важной задачей анализа является объяснение механиз­ма изменения уровней ряда. Для ее решения обычно прибегают к регрессионному анализу. Наконец, описание изменения времен­ного ряда и объяснение механизма формирования ряда часто ис­пользуются для статистического прогнозирования, которое в боль­шинстве случаев сводится к экстраполяции обнаруженных тен­денций развития.

Анализ временного ряда и последующий прогнозирование его развития может использоваться для:

- планирования в экономике, производстве, торговле;

- управления и оптимизации, протекающих в обществе социально-экономических процессов;

- частичного управления важными параметрами демографических процессов и экологической ниши общества;

- принятия оптимальных решений в бизнесе.

В данной лабораторной работе анализ временного ряда будет производиться в статистическом пакете «MINITAB».

     Minitab позволяет анализировать данные зависящие от времени (временные ряды), выявлять основные закономерности этих зависимостей и на основе полученных моделей прогнозировать будущие значения для этих рядов.

Minitab включает следующие основные виды анализа временных рядов:

Trend Analysis - анализ линии тренда с использованием четырех типов аппроксимирующих кривых.

Decomposition - классическая декомпозиция временных рядов.

Moving Average - вычисление скользящего среднего.

Exp Smoothing - экспоненциальное сглаживание временного ряда.

Lag - смещение рядов на заданное значение.

Autocorrelation - вычисление автокорреляционной функции.

Cross Correlation - вычисление кросскорреляционной функции.

ARIMA - оценивание модели Бокса-Дженкинса.

Понятие тенденция развития не имеет достаточно четкого опре­деления. Обычно тенденцию стремятся представить в виде более или менее гладкой кривой, которой соответствует некоторая функция времени. Эта кривая, назовем ее трендом, характеризует основ­ную закономерность движения во времени и в известной мере (но не полностью) свободна от случайных воздействий. Тренд опи­сывает некоторую усредненную для достаточно протяженного пе­риода наблюдения тенденцию развития во времени. В большин­стве случаев полученная траектория связывается исключительно с ходом времени. Предполагается, что с помощью переменной время можно выразить влияние всех основных факторов. Меха­низм их влияния в явном виде не учитывается.

Для анализа линии тренда в статистическом пакете «MINITAB» необходимо выполнить следующую операцию: Stat > Time Series > Trend Analysis. На мониторе появится следующее диалоговое окно (Рис 1.1):

 

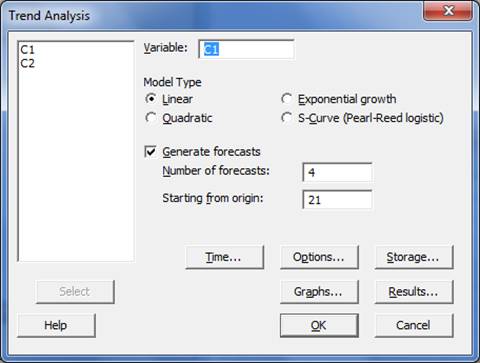
Рисунок 1.1 – Диалоговое окно «Анализ линии тренда»

 

Диалоговое окновключает в себя следующие параметры:

Variable: вводится идентификатор (название) столбца в таблице с исследуемым временным рядом.

Model Type: определяется тип модели для аппроксимации тренда временного ряда. В используемой программе Minitab рассматриваются следующие четыре типа моделей:

 - Linear – линейная;

 - Quadratic – квадратическая;

 - Exponential growth - экспоненциального роста;

 - S-Curve (Pearl-Reed logistic)- логистическая S – кривая.

Generate forecasts: Отмечается при необходимости просчитать прогнозные значения, на графике эти точки отмечаются красным цветом.

Number of forecasts: Вводится число точек для прогноза.

Starting from origin: Вводится положительное число, определяющее с какой точки начинать считать прогнозные значения. Если эта позиция остается не заполненной Minitab начинает считать прогнозные значения, начиная с последней точки исходного временного ряда. Например, если в примере 1 необходимо сделать прогноз производства автомобилей на три года вперед, начиная с последнего года, т. е. с 22-го по счету, то в эту позицию вводят число 21 и программа подсчитает прогноз в точках 22, 23, 24.

Title: Вводится вами заданный заголовок для выводимого графика.

Результат проведенного исследования Minitab выводит в виде графика, на котором показаны исходные данные, аппроксимирующая их линия тренда и рассчитанные прогнозные значения для этого ряда. В качестве оценок точности аппроксимации и вычисленного прогноза Minitab использует следующие три показателя:

MAPE - средняя абсолютная ошибка в процентах;

MAD - среднее абсолютное отклонение;

MSD - среднеквадратическое отклонение. Близко по своей структуре к среднеквадратической ошибке, но не зависит от числа степеней свободы для разных моделей, поэтому может быть использовано для сравнения точности разных моделей.

Вычисляются эти оценки точности следующим образом:

          Вычисляются эти оценки точности следующим образом:

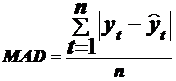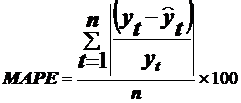               ; , где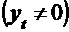

            ;   

 

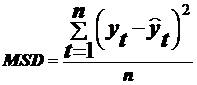Определение типа модели для аппроксимации тренда временного ряда – одна из наиболее сложных задач анализа временных рядов. Оценка коэффициентов уравнения тренда осуществляется по методу наименьших квадратов (МНК).

Наиболее часто в экономике при аппроксимации тренда используются следующие виды функций:

- линейная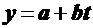             

- параболическая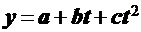   

- степенная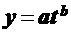             

- экспоненциальная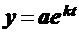

- функцию Гомперца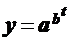

- логистическая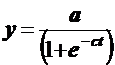      

 

Пример 1: Рассмотрим динамику производства автомобилей и цен на них в мире за 1990 –2010 гг., данные представлены в таблице 1.1. Необходимо определить тип модели для аппроксимации имеющихся временных рядов. В качестве критерия оптимальности выбора модели воспользуемся показателем MSD - среднеквадратическим отклонением.

 

Таблица 1.1 -

Годы	Производство автомобилей	Цены на автомобили	Годы	Производство автомобилей	Цены на автомобили
1990	100	100	2001	135	101
1991	78	131	2002	183	102
1992	91	148	2003	174	103
1993	130	114	2004	191	104
1994	139	89	2005	165	108
1995	130	84	2006	143	122
1996	139	85	2007	161	155
1997	122	83	2008	165	168
1998	143	108	2009	204	152
1999	161	109	2010	200	133
2000	152	102

 

Статистический пакет Minitab рассматриваются следующие четыре типа моделей: линейная, квадратическая, экспоненциального роста, логистическая S – кривая. Выполним расчеты по каждой из моделей для обоих временных рядов и представим данные расчетов в таблице 2.

 

Таблица 1.2 -

Вид модели	MSD
	Производство автомобилей	Цены на автомобили
линейная	296.219	460.058
квадратическая	272.670	258.870
экспоненциального роста	331.586	452.138
логистическая S – кривая	281.557	нет данных

 

Наиболее точно описывают имеющиеся данные квадратическая модель, так как среднеквадратическое отклонение (MSD) у этой модели наименьшее. Уравнения тренда, описывающие данные временные ряды имеют вид:

- для производства автомобилей:

         Yt = 84,5 + 7,89*t - 0,148*t^2

  

 

- для цены на автомобили:

          Yt = 130,9 - 7,73*t + 0,434*t^2

 

В результате выполнения операции: Stat > Time Series > Trend Analysis и заполнения диалогового окна на экране появятся графики, которые показаны на рисунке 1.2. На графиках видно, что выбранные нами модели тренда достаточно точно описывают имеющиеся временные ряды.