Тема: «Теория функции комплексного переменного»
| 4 | Задача 1. Решить уравнение  , построить корни на комплексной плоскости.
Задача 2. Найти аналитическую функцию , построить корни на комплексной плоскости.
Задача 2. Найти аналитическую функцию  по заданной ее мнимой части: по заданной ее мнимой части:  .
Задача 3Найти вычеты функции .
Задача 3Найти вычеты функции  относительно ее полюсов
Задача 4. Пользуясь основной теоремой о вычетах, вычислить интеграл по замкнутому контуру: относительно ее полюсов
Задача 4. Пользуясь основной теоремой о вычетах, вычислить интеграл по замкнутому контуру:  , где , где  – окружность – окружность  .
Задача 5. Найти изображение .
Задача 5. Найти изображение  заданного оригинала заданного оригинала  .
Задача 6. Найти оригинал .
Задача 6. Найти оригинал  по изображению по изображению 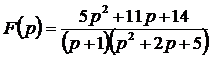 .
Задача 7. Решить дифференциальные уравнения операторным методом, проверить с помощью встроенной функции и построить график:
1) .
Задача 7. Решить дифференциальные уравнения операторным методом, проверить с помощью встроенной функции и построить график:
1)  ;
2) ;
2)  ; ; 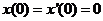 .
Задача 8. Разложить в ряд Фурье следующие периодические функции .
Задача 8. Разложить в ряд Фурье следующие периодические функции
 , если , если  Построить на одном графике функцию и разложение.
Построить на одном графике функцию и разложение.
|
Вычислительная работа №7
Тема: «Теория функции комплексного переменного»
| 5 | Задача 1. Решить уравнение  , построить корни на комплексной плоскости.
Задача 2. Найти аналитическую функцию , построить корни на комплексной плоскости.
Задача 2. Найти аналитическую функцию  по заданной ее действительной части: по заданной ее действительной части:  .
Задача 3Найти вычеты функции .
Задача 3Найти вычеты функции  относительно ее полюсов
Задача 4. Пользуясь основной теоремой о вычетах, вычислить интеграл по замкнутому контуру: относительно ее полюсов
Задача 4. Пользуясь основной теоремой о вычетах, вычислить интеграл по замкнутому контуру:  , где , где  – окружность – окружность  .
Задача 5. Найти изображение .
Задача 5. Найти изображение  заданного оригинала заданного оригинала  .
Задача 6. Найти оригинал .
Задача 6. Найти оригинал  по изображению по изображению  .
Задача 7. Решить дифференциальные уравнения операторным методом, проверить с помощью встроенной функции и построить график:
1) .
Задача 7. Решить дифференциальные уравнения операторным методом, проверить с помощью встроенной функции и построить график:
1)  ;
2) ;
2) 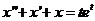 ; ; 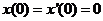 .
Задача 8. Разложить в ряд Фурье следующие периодические функции .
Задача 8. Разложить в ряд Фурье следующие периодические функции
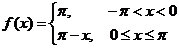 , если , если  Построить на одном графике функцию и разложение.
Построить на одном графике функцию и разложение.
|
Вычислительная работа №7
 2018-02-14
2018-02-14 169
169








