Второе уравнение Максвелла

Определение переменного электромагнитного поля

Под переменным электромагнитным полем понимают совокупность изменяющихся во времени и взаимно связанных и обуславливающих друг друга электрического и магнитного полей. Оно определяется двумя векторными величинами – напряженностью электрического поля  и напряженностью магнитного поля .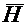

Переменное электромагнитное поле является одним из видов материи. Оно обладает энергией, массой, количеством движения, может превращаться в другие виды материи и самостоятельно существовать в виде электромагнитных волн. Любые возмущения поля в диэлектрике с огромной скоростью, для вакуума равной примерно 3·10⁸ м/с, передаются на большие расстояния.

При исследовании процессов в переменном электромагнитном поле пользуются уравнениями Максвелла.

Первое уравнение Максвелла

Первое уравнение Максвелла представляет собой закон полного тока в дифференциальной форме

(44.1)

Так как плотность полного тока определяется суммой плотности тока проводимости  и плотности тока смещения , то первое уравнение Максвелла в общем случае имеет вид:

(44.2)

Для сред с постоянной диэлектрической проницаемостью

(44.3)

Физический смысл этого уравнения заключается в том, что вихревое магнитное поле возбуждается как токами проводимости, так и изменяющимся во времени электрическим полем.

Для идеальных диэлектриков с проводимостью  имеем:

(44.4)

Первое уравнение Максвелла устанавливает зависимость между изменением во времени напряженности электрического поля и изменением в пространстве напряженности магнитного поля и указывает на то, что электромагнитное поле всегда находится в движении.

Второе уравнение Максвелла

Второе уравнение Максвелла представляет собой дифференциальную форму закона электромагнитной индукции, согласно которому в витке при изменении сцепленного с ним магнитного потока наводится ЭДС, равная

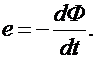
Максвелл обобщил этот закон, указав, что изменяющийся во времени магнитный поток возбуждает электрическое поле и при отсутствии витка.

В поле с индукцией  магнитный поток сквозь произвольную поверхность S, ограниченную контуром L, равен:

Если напряженность индуцированного электрического поля обозначить Е, то наведенная в контуре ЭДС .

Будем считать, что контур L и поверхность S неподвижны и не деформируются, тогда

Положительные направления обхода контура L и положительное направление нормали к поверхности S выбираются так, чтобы они образовали правовинтовую систему.

Частные производные введены потому, что ЭДС может индуцироваться не только за счет изменения магнитного потока во времени, но и за счет движения или деформации контура.

На основании теоремы Стокса можно преобразовать циркуляцию

Следовательно

Равенство интегралов справедливо для любой поверхности S, поэтому подынтегральные функции равны и

(44.5)

Полученное выражение называют вторым уравнением Максвелла.

Физический смысл его заключается в утверждении, что изменяющееся во времени магнитное поле возбуждает вихревое электрическое поле.

Так как 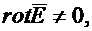 то линии вектора  могут быть замкнутыми, причем они должны охватывать линии вектора . Направление линий векторов и  показаны на рисунке 44.1 для случая, когда 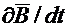< 0.

В электростатическом поле, которое является безвихревым,  Линии вектора  всегда разомкнуты, они начинаются у положительных зарядов и заканчиваются у отрицательных.

Для сред с постоянной магнитной проницаемостью второе уравнение Максвелла принимает вид:

(44.13)

Второе уравнение Максвелла устанавливает зависимость между изменением во времени напряженности магнитного поля и изменением в пространстве напряженности электрического поля.