ВОПРОСЫ К ЭКЗАМЕНУ
1. Частное и общее решение дифференциальных уравнений (ДУ) 1-го порядка. Теорема существования и единственности решения задачи Коши для ДУ 1-го порядка.
2. Основные типы ДУ 1-го порядка и методы их решения.
3. Частное и общее решение ДУ 2-го порядка. Теорема существования и единственности решения задачи Коши для ДУ 2-го порядка.
4. Теорема существования и единственности решения задачи Коши для ДУ 2-го порядка.
5. Линейная независимость функций на отрезке. Фундаментальная система решений линейного однородного ДУ, ее свойства. Определитель Вронского.
6. Теорема о структуре решения линейного однородного ДУ.
7. Теорема о структуре решения линейного неоднородного ДУ.
8. Построение фундаментальной системы решений для линейных ДУ 2-го порядка с постоянными коэффициентами (случай положительного, нулевого и отрицательного дискриминанта характеристического уравнения).
9. Метод вариации произвольных постоянных для нахождения частного решения линейного неоднородного ДУ.
10. Сходимость числового ряда. Необходимый признак сходимости. Линейные свойства сходящихся рядов.
11. Признаки сравнения числовых рядов с положительными членами, связанный с неравенствами.
12. Признаки сравнения числовых рядов с положительными членами, связанный с пределом.
13. Признак Даламбера сходимости числового ряда.
14. Радикальный признак Коши сходимости числового ряда.
15. Интегральный признак Коши сходимости числового ряда. Ряды Дирихле.
16. Абсолютная и условная сходимость знакопеременных числовых рядов.
17. Признак Лейбница сходимости знакочередующихся рядов. Оценка остатка знакочередующегося ряда, сходящегося по признаку Лейбница.
18. Функциональный ряд, область его сходимости. Равномерная сходимость. Признак Вейерштрасса равномерной сходимости ряда. Свойства равномерно сходящихся рядов.
19. Степенной ряд. Теорема Абеля. Радиус сходимости степенного ряда.
20. Свойства степенных рядов. Почленное дифференцирование и интегрирование степенных рядов.
21. Ряд Тейлора. Необходимое и достаточное условие представимости функции рядом Тейлора.
22. Разложение основных элементарных функций в степенные ряды.
| 1 Частное и общее решение дифференциальных уравнений (ДУ) 1-го порядка. Множество функций, удовлетворяющих данному уравнению, имеющее вид у=f(x;C), называется общим решением ДУ.Для того чтобы выделить единственное решение, нужно задать начальные условия.Задача отыскания решения y = y(x) уравнения F(x, y, y ') = 0, удовлетворяющего условию y(x0) = y0, называется задачей Коши.Любое конкретное решение y = y(x) называется частным решением ДУ. Теорема существования и единственности решения задачи Коши для ДУ 1-го порядка. Если в уравнении y’=f(x.y) функция f(x.y) и ее частная производная непрерывны в некоторой области D, содержащей точку M0(x0,y0), то существует единственное решение y=ф(х) этого уравнения, удовлетворяющее начальному условию у(х0)=у0 | 12 Признаки сравнения числовых рядов с положительными членами, связанный с пределом.
Пусть  то ряд то ряд  и и  ведут себя одинаково.
Док-во: 1) Пусть ряд ведут себя одинаково.
Док-во: 1) Пусть ряд  сходится, сходится,  2) Пусть ряд
2) Пусть ряд  расходится, расходится, 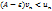 => ряд => ряд  расходится. расходится.
|
2 Основные типы ДУ 1-го порядка и методы их решения.
1. C разделяющимися переменными: уравнение вида  , Метод решения носит название разделения переменных. Уравнение перепишем в виде , Метод решения носит название разделения переменных. Уравнение перепишем в виде   . Тогда . Тогда 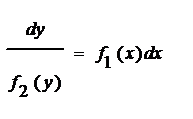 . Интегрируем . Интегрируем  , где , где  .
2. Линейные дифференциальные уравнения I-го порядка; yравнение вида .
2. Линейные дифференциальные уравнения I-го порядка; yравнение вида
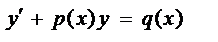 где p(x), q(x) - непрерывные функции.
Методы решения л.д.у. первого порядка.
1.Метод вариации постоянной. Находим общее решение однородного уравнения где p(x), q(x) - непрерывные функции.
Методы решения л.д.у. первого порядка.
1.Метод вариации постоянной. Находим общее решение однородного уравнения  .Перепишем в виде уравнения с разделенными переменными .Перепишем в виде уравнения с разделенными переменными  , , 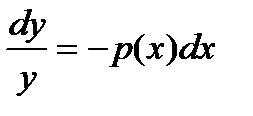 . Интегрируем правую и левую часть уравнения, получим . Интегрируем правую и левую часть уравнения, получим  ., .,  . Подставляем это решение в неоднородное уравнение, при c=с(x). Дифференцируем y и подставляем . Подставляем это решение в неоднородное уравнение, при c=с(x). Дифференцируем y и подставляем  в неоднородное уравнение. Решаем полученное уравнение и находим с(x). Полученное выражение для с подставляем в в неоднородное уравнение. Решаем полученное уравнение и находим с(x). Полученное выражение для с подставляем в  .
2. Метод подстановки. .
2. Метод подстановки. 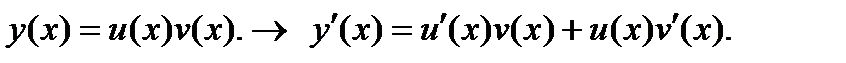 Подставим эти выражения в исходное уравнение: Подставим эти выражения в исходное уравнение:
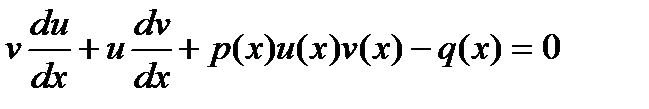 . Выберем u(x) такое), чтобы . Выберем u(x) такое), чтобы  .
Найдем u(x) из уравнения .
Найдем u(x) из уравнения  , применив метод разделяющих переменных. Получим , применив метод разделяющих переменных. Получим 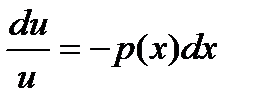 , ,  . Выберем частное решение (например, при с =1 и . Выберем частное решение (например, при с =1 и  , подставим в л.д.у. и получим , подставим в л.д.у. и получим  . .  3. Неполные д.у.первого порядка: ДУ первого порядка
3. Неполные д.у.первого порядка: ДУ первого порядка  называется неполным, если функция называется неполным, если функция  явно зависит только от одной переменной: либо от x, либо от y.
1. явно зависит только от одной переменной: либо от x, либо от y.
1.  2 2  . Методом разделения переменных определяется неизвестная функция . Методом разделения переменных определяется неизвестная функция  (или (или 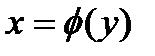 ). Уравнение ). Уравнение  называется автономным Д.У., такие уравнения имеют место в теории математического моделирования. Особый интерес представляют так называемые точки равновесия, или стационарные точки: нули функции называется автономным Д.У., такие уравнения имеют место в теории математического моделирования. Особый интерес представляют так называемые точки равновесия, или стационарные точки: нули функции  , где , где 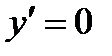 . .
| 13 Признак Даламбера сходимости числового ряда. Если члены ряда  таковы, что существует конечный предел таковы, что существует конечный предел   Док-во Док-во  1)Пусть q<1 при n>N
1)Пусть q<1 при n>N  <q q+ <q q+  <1 сходится
2) Пусть q>1 тогда q- <1 сходится
2) Пусть q>1 тогда q-  >1 => >1 =>  >q- >q-  >1 => >1 =>  > >  => =>  возрастающая последовательность=> возрастающая последовательность=>  По необходимому признаку сходимости ряд По необходимому признаку сходимости ряд 
|
3 Частное и общее решение ДУ 2-го порядка. Теорема существования и единственности решения задачи Коши для ДУ 2-го порядка.
Д.У. второго порядка называется уравнение вида  ,где х - независимая переменная, у – искомая функция, ,где х - независимая переменная, у – искомая функция, 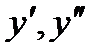 - производные. Общим решением уравнения - производные. Общим решением уравнения 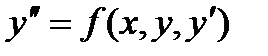 в некоторой области D называется функция в некоторой области D называется функция  , если она является решением этого уравнения при любых постоянных, которые могут быть определены единственным образом при заданных начальных условиях. Частным решением называется общее решение этого уравнения при фиксированных значениях постоянных , если она является решением этого уравнения при любых постоянных, которые могут быть определены единственным образом при заданных начальных условиях. Частным решением называется общее решение этого уравнения при фиксированных значениях постоянных  - - 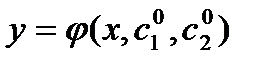 .
Теорема существования и единственности решения задачи Коши для ДУ 2-го порядка.
Пусть функция .
Теорема существования и единственности решения задачи Коши для ДУ 2-го порядка.
Пусть функция  и её частные производные и её частные производные   непрерывны в некоторой области D пространства переменных непрерывны в некоторой области D пространства переменных 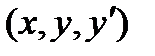 . Тогда для любой внутренней точки . Тогда для любой внутренней точки  этой области существует единственное решение уравнения, удовлетворяющее условиям этой области существует единственное решение уравнения, удовлетворяющее условиям 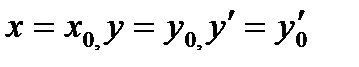 . .
| 14 Радикальный признак Коши сходимости числового ряда.  1) Пусть q<1
1) Пусть q<1  => q+ => q+  =q<1 =q<1  <q=> <q=>  < <  сходящаяся геометрическая прогрессия. => ряд сходящаяся геометрическая прогрессия. => ряд  сходится
2) Пусть q>1 q- сходится
2) Пусть q>1 q-  =q>1 => =q>1 =>  >q>1 => >q>1 =>   расходящаяся геомет. Прогрессия=> ряд расходящаяся геомет. Прогрессия=> ряд  расходится расходится
|
| 4 Теорема существования и единственности решения задачи Коши для ДУ 2-го порядка. y''=F(x,y,y''); y(x0)=y0, y'(x0)=y0' Если в некоторой области D переменных (x,y,y')функция f(x,y,y') и df/dy, df/dy' существуют и непрерывны, то задача Коши для любой точки M0(x0,y0,y0')ϵD имеет решение, причем единственное. Теор. Коши для ЛН ДУ2го пор. y''=f(x,y,y''); y''=b(x)-a1(x)y'-a2(x)y; df/dy=-a2(x); df/dy'=-a1(x) Если функ-ии a1(x), a2(x), b(x) определены и непрерывны на некотором интервале xϵ(α, β), то для любого x0ϵ(α, β) существует единственное решение ДУ, удовлетворяющее условию y(x0)=y0, y'(x0)=yo' для любых y0, y0'. | 15 Интегральный признак Коши сходимости числового ряда. Ряды Дирихле. Пусть функция f(x) положительна и монотонна при x≥1, и пусть для всех n С N имеет место равенство f(n)=|  |. Тогда числовой ряд |. Тогда числовой ряд  сходится(т.е. ряд сходится(т.е. ряд  сходится абсолютно) или расходится одновременно с несобственным интегралом сходится абсолютно) или расходится одновременно с несобственным интегралом  Ряды Дирихле:
Ряды Дирихле:
|
| 5 Линейная независимость функций на отрезке. Фундаментальная система решений линейного однородного ДУ, ее свойства. Определитель Вронского. * y''+a1(x)y'+a2(x)y=0 Опр.Два частных решения y1(x) и y2(x) линейного однородного ДУ 2го пор. образуют фуедаментальную систему решений на интервале(α, β), если ни в одной точке указанного интервала определитель Вронского не обращается в ноль. W(x)=|■(y1(x)&y2(x)@y1'(x)&y2^' (x))| Опр.Две фун-ии y1(x) и y2(x) называются линейно-зависимыми на интерв. (α, β), если существуют такие числа ℷ1 и ℷ2, из которых хотя бы одно не равно нулю, что для всех x, xϵ(α, β), имеет место ℷ1y1(x)+ℷ2y2(x)=0. Если это рав-во выполн. для всех x и интерв. (α, β), ℷ1=ℷ2-0, то y1(x) и y2(x) - линейно-независимые. y1(x) и y2(x) линейн-независ., если они непропорциональны; и если они непропорциональны, то они линейн.-независ. Теор. Если y1(x), y1(x) лин.-завис. на (α, β), то опред. Вронского, составленный из этих функ-ий равен нулю на этом интервале. Теор. Если решение y1(x), y2(x) ДУ * лин.-независ. на (α, β), то опред. Вронского не равен нулю на данном интервале. Соотв.: Если 1 частн. реш. y1(x), y2(x) ДУ* лин.-независ., то это эквивалентно тому, что они непропорциональны и образуют Ф.С.Р Если 2 частн. реш. лин-завис, это эквивалентно их пропорциональности и они не образуют Ф.С.Р | 16 Абсолютная и условная сходимость знакопеременных числовых рядов. Ряд  называется абсолютно сходящимся, если сходится ряд из модулей членов этого ряда, т.е. сходится называется абсолютно сходящимся, если сходится ряд из модулей членов этого ряда, т.е. сходится  ряд. Если ряд ряд. Если ряд  сходится, а сходится, а  расходится, то ряд расходится, то ряд  называется условно сходящимся. называется условно сходящимся.
|
| 6 Теорема о структуре решения линейного однородного ДУ. * y''+a1(x)y'+a2(x)y=0 Если два частных решения y1(x) и y2(x)уравнения * образуют на интервале (α, β) фундамент. систему решений, то функция y(x)=C1y1(x)+C2y2(x) является общим решением данного ДУ. При этом коэффициенты a1(x) и a2(x) непрерывны на интервале (α, β). | 17 Признак Лейбница сходимости знакочередующихся рядов. Оценка остатка знакочередующегося ряда, сходящегося по признаку Лейбница.
Пусть  - знакочередующийся ряд.
Если - знакочередующийся ряд.
Если  и и  , то ряд , то ряд  сходится.
Из теоремы Лейбница вытекает следствие, позволяющее оценить погрешность вычисления неполной суммы ряда: сходится.
Из теоремы Лейбница вытекает следствие, позволяющее оценить погрешность вычисления неполной суммы ряда:
 Остаток сходящегося знакочередующегося ряда
Остаток сходящегося знакочередующегося ряда  , будет по модулю меньше первого отброшенного слагаемого: , будет по модулю меньше первого отброшенного слагаемого: 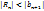 . .
|
| 7 Теорема о структуре решения линейного неоднородного ДУ. ** y''+a1(x)y'+a2(x)y=f(x) * y''+a1(x)y'+a2(x)y=0 Если ý(x) - любое частное решение лин. неодноро. ДУ **, то ощее решение неоднор. У записывается в виде: y=Y(x)+ý(x), Y(x) - общ. реш. однор ДУ* | 18 Функциональный ряд, область его сходимости. Равномерная сходимость. Признак Вейерштрасса равномерной сходимости ряда. Свойства равномерно сходящихся рядов. U_1 (x)+U_2 (x)+U_3 (x)+⋯+U_n (x)+U_(n+1) (x)+⋯ (от U_1 (x)до U_n (x)=S_n) (1) Обл сход-множество знач. x_i для кот ряд сход. Обл расход- --‖--ряд расход. lim┬(n→∾)〖S_n (x)=S(x)-сумма ряда,определяемая на обл сход этого ряда〗. ∀ε>0 ∃ N(ε,x): ∀n>N⇒|S_n (x)-S(x)|<ε. Ряд (1) сход равномерно к ф-и S(x) на обл D, если ∀x∊D. ∀ε>0 ∃ N(ε): ∀n>N⇒|S_n (x)-S(x)|<ε Признак Вейерштрасса: пусть ряд (1) ∀x∊D удовл усл U_(n+1) (x)≤a_n ∀n где a_n-сходящийся числовой ряд, тогда ряд (1) сход. Равномерно на обл D. При этом a_n называется мажоритарным для ряда (1). Св-ва равномерносход рядов:∑_(n=1)^∞▒〖U_n (x)=f(x)-ряд равномерносход на обл D〗 1Если U_n (x)-непрерывные ф-и на обл D, то сумма ряда S(x) непрерывна на обл D 2Если U_n (x)-интегрируемая ф-я на обл D, то ∑_(n=1)^∞▒〖∫▒U_n (x)dx=∫▒〖S(x)〗〗 3Если U_n (x)-диффер-ая ф-я на обл D и ряд U_xпроизводных сход равномерно на обл D, то ∑_(n=1)^∞▒〖U^' (x)=S^' (x)〗 |
| 8 Построение фундаментальной системы решений для линейных ДУ 2-го порядка с постоянными коэффициентами (случай положительного, нулевого и отрицательного дискриминанта характеристического уравнения). Пусть y''+py'+qy=b(x), p и q - числа. y''+py'+qy=0 - соответствующее ЛОДУ. y(x) = e^λx y'(x) =λ*e^λx y''(x) =λ^2*e^λx λ^2*e^λx+pλ*e^λx+qe^λx=0 |∶e^λx λ^2+pλ+q=0 - характеристическое уравнение 1) D>0: λ_1≠λ_2 - 2 действительных корня ФСР: y_1 (x)= e^(λ_1 x); y_2 (x)= e^(λ_2 x) Y_оо=C_1 e^(λ_1 x)+C_2 e^(λ_2 x) 2) D=0: λ_1=λ_2=λ ФСР: y_1 (x)= e^λx; y_2 (x)= 〖xe〗^λx Y_оо=C_1 e^λx+C_2 〖xe〗^λx 3) D<0: λ_1,2=α±βi ФСР: y_1 (x)= e^αx*cosβx; y_2 (x)= e^αx*sinβx Y_оо=C_1 e^αx*cosβx+C_2 e^αx*sinβx | 19 Степенной ряд. Теорема Абеля. Радиус сходимости степенного ряда. a_0+a_1 (x-a)+a_2 〖(x-a)〗^2+a_3 〖(x-a)〗^3+...+a_n 〖(x-a)〗^n+a_(n+1) 〖(x-a)〗^(n+1)+...(1) При a=0 a_0+a_1 x+a_2 x^2+a_3 x^3+...+a_n x^n+a_(n+1) x^(n+1)+...(2) при x=0 ряд сход. Теорема Абеля: 1 Если ряд(2) сход при x=x_0, то он сход ∀|x|<|x_(0) | 2 Если ряд(2) расход при x=x_1, он расход ∀|x|>|x_(1) | 3 ∀ ряда(2) сущ числ R≥0 (радиус сход) такое, что при |x|<R ряд сход, при |x|>R расход, при |x|=R может сходиться, может расход. Док-во: Пусть ряд(2) при x=x_0 сход. ∑_(n=0)^∞▒〖a_n x_0^n 〗-числ ряд⇒lim┬(n→∞)〖a_n x_0^n=0 〗 a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4+a_5 x^5+...+a_n x^n+...=a_0+a_1 x_0 x/x_0 +a_2 x_0^2 (x/x_0)^2+a_3 x_0^3 (x/x_0)^3+...+a_n x_0^n (x/x_0)^n+... |a_0 |+|a_1 x_0 ||x/x_0 |+|a_2 x_0^2 | |x/x_0 |^2+|a_3 x_0^3 | |x/x_0 |^3+...+|a_n x_0^n | |x/x_0 |^n+... M+m|x/x_0 |+M|x/x_0 |^2+M|x/x_0 |^3+...+M|x/x_0 |^n+...геом прогрессия. q=|x/x_0 |<1⇒ ряд из модулей ряда(2) сход по пр-ку ср-я, связ. с нер-вом⇒ряд(2) сход по абс пр-ку сход |
9 Метод вариации произвольных постоянных для нахождения частного решения линейного неоднородного ДУ. Метод вариации произвольных постоянных:
Для отыскания частного решения линейного неоднородного дифференциального уравнения второго порядка  с переменными коэффициентами с переменными коэффициентами

 Потребуем, чтобы
Потребуем, чтобы  удовлетворял удовлетворял  : :



 План решения методом вариации произвольных постоянных:
1)Составляем систему
План решения методом вариации произвольных постоянных:
1)Составляем систему  для отыскания для отыскания  и и  2)По найденным
2)По найденным  и и  восстанавливаем восстанавливаем 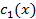 и и  3)Формируем
3)Формируем 
| 20 Свойства степенных рядов. Почленное дифференцирование и интегрирование степенных рядов.
1)При почленном интегрировании и дифференцировании радиус сходимости степенного ряда не меняется.
1.1 Интегрирование
 q
| q
| 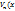 )|= )|= 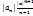 ; | ; | 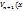 )|= )|= 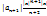 q q
 q
1.2 Дифференцирвание q
1.2 Дифференцирвание
 q
| q
|  )|= )|=  ; | ; |  )|= )|= 
 q
2) r>0, r<R, тогда на [-r;r] рядq q
2) r>0, r<R, тогда на [-r;r] рядq  сходится равномерно
3) На обл. абсол. сходимости рядq сходится равномерно
3) На обл. абсол. сходимости рядq  сводится к непрерывной функции
4) Для сводится к непрерывной функции
4) Для  x x  (-R;R) рядq (-R;R) рядq  можно почленно интегрировать и дифференцировать можно почленно интегрировать и дифференцировать
|
10 Сходимость числового ряда. Необходимый признак сходимости. Линейные свойства сходящихся рядов.
Пусть  - числовой ряд, а - числовой ряд, а  - частичная сумма ряда. Тогда, если - частичная сумма ряда. Тогда, если  , то есть конкретному числу, то числовой ряд , то есть конкретному числу, то числовой ряд  сходится.
Необходимый признак сходимости:
Если ряд сходится.
Необходимый признак сходимости:
Если ряд  сходится, то сходится, то 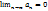 . НО! Если . НО! Если 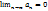 , то ряд , то ряд  может как сходиться, так и расходиться.
Линейные свойства сходящихся рядов:
1) Если ряд может как сходиться, так и расходиться.
Линейные свойства сходящихся рядов:
1) Если ряд  сходится, то сходится ряд сходится, то сходится ряд  . 2) Если ряд . 2) Если ряд  и ряд и ряд  сходятся, то ряд сходятся, то ряд  тоже сходится. тоже сходится.
| 21 Ряд Тейлора. Необходимое и достаточное условие представимости функции рядом Тейлора
f(x)=f(a)+  (a)(x-a)+ (a)(x-a)+  (a) (a)  q
f(x) – ряд Тейлора
f(x)-Sn(x)=Rn(x)-остаточный член ряда Тейлора
Для сходимостя рТ к функции f(x) необходимо и достаточно, чтобы q
f(x) – ряд Тейлора
f(x)-Sn(x)=Rn(x)-остаточный член ряда Тейлора
Для сходимостя рТ к функции f(x) необходимо и достаточно, чтобы  =0
Необходимость:
Пусть f(x)=сумма рТ, =0
Необходимость:
Пусть f(x)=сумма рТ,  =f(x) =f(x)
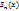 =f(x)-Rn(x)=> =f(x)-Rn(x)=>  f(x)-Rn(x))=f(x)
F(x)- f(x)-Rn(x))=f(x)
F(x)-  Rn(x)=f(x)=> Rn(x)=f(x)=>  Rn(x)=0
Достаточность:
Пусть Rn(x)=0
Достаточность:
Пусть  Rn(x)=0 Rn(x)=0
 = =  f(x)-Rn(x))=f(x) f(x)-Rn(x))=f(x)
 , c , c 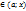 -остаточный член в форме Лагранжа -остаточный член в форме Лагранжа
|
11 Признаки сравнения числовых рядов с положительными членами, связанный с неравенствами.
Признаки сравнения числовых рядов с положительными членами, связанный с неравенствами.
Пусть даны два ряда с положительными членами  и и  , причём члены первого ряда не превосходят соответствующих членов второго, т.е. , причём члены первого ряда не превосходят соответствующих членов второго, т.е. 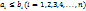 . Тогда из сходимости ряда . Тогда из сходимости ряда  следует сходимость следует сходимость  , а из расходимости ряда , а из расходимости ряда  – расходимость – расходимость  . .
| 22 Разложение основных элементарных функций в степенные ряды





 Биноминальный ряд
Биноминальный ряд
|
j
 2018-02-13
2018-02-13 534
534






