Ші тамаша шек
Теорема. 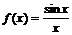 функциясы x=0 нүктеде анықталмаған, бірақ
функциясы x=0 нүктеде анықталмаған, бірақ 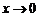 жағдайда шегі бар және
жағдайда шегі бар және 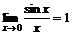 Осы шекті бірінші тамаша шек деп атайды. Бірінші тамаша шек салдары:
Осы шекті бірінші тамаша шек деп атайды. Бірінші тамаша шек салдары:
1) 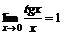 , 2)
, 2) 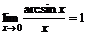 , 3)
, 3) 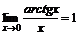 .
.
Мысал. а) 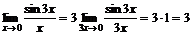 .
.
б) 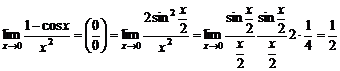 .
.
Екінші тамаша шек
Теорема. 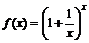 функциясының
функциясының 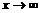 жағдайда шегі бар және
жағдайда шегі бар және 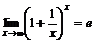 . Осы шекті екінші тамаша шек деп атайды. Мұндағы
. Осы шекті екінші тамаша шек деп атайды. Мұндағы 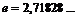 иррационал саны Эйлер саны екені белгілі.
иррационал саны Эйлер саны екені белгілі.
Екінші тамаша шек салдары:
1) 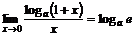 , a=e болғанда
, a=e болғанда 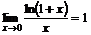 ;
;
2) 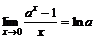 , a=e болғанда
, a=e болғанда 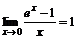 ;
;
3) 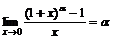 Мысал. а)
Мысал. а) 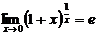 екенін көрсет.
екенін көрсет.
Шешуі. 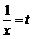 деген білгілеу енгізейік. Осыдан
деген білгілеу енгізейік. Осыдан 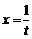 . Және де
. Және де 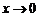 кезде
кезде 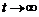 . Енді шек есептесек
. Енді шек есептесек 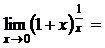
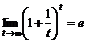 .
.
б) 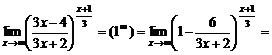
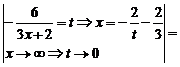
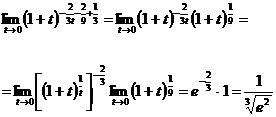
Лопиталь ережесі арқылы анықталмағандықты ашу. Теорема (Лопиталь ережесі). f(x) және g(x) функциялары 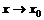 (
(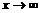 ) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады:
) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады: 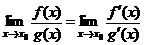 . Лопиталь ережесін қолданып ектерді есмептейік.
. Лопиталь ережесін қолданып ектерді есмептейік.
1. 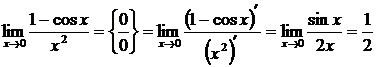 .
.
2. 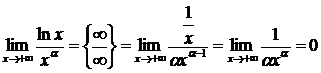
3. 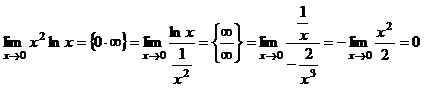 .
.
Үшінші мысалда Лопиталь ережесін бірден қолдануға келмейді. Сондықтан, алгебралық түрлендіру көмегімен 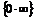 түріндегі анықталмағандықты
түріндегі анықталмағандықты 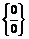 немесе
немесе 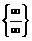 түріндегі анықталмағандықтарға келтіреміз. Осы мақсатпен х 2 бөлімнің бөліміне түсірілді.
түріндегі анықталмағандықтарға келтіреміз. Осы мақсатпен х 2 бөлімнің бөліміне түсірілді.
4. 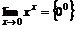 . Айталық
. Айталық 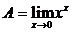 деп белгілеп, теңдеудің екі жағын логарифмдейік. Теңдеудіңоңжағынесептейік:
деп белгілеп, теңдеудің екі жағын логарифмдейік. Теңдеудіңоңжағынесептейік: 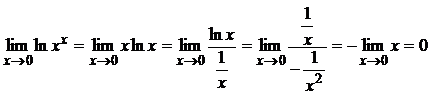
Функция дифференциалы
Функция шегінің анықтамасына сүйеніп туынды табу 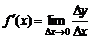 формуласын мынадай түрде көшіріп жазуға болады:
формуласын мынадай түрде көшіріп жазуға болады: 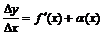 ,
,
мұндағы 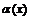 - ақырсыз аз шама, яғни
- ақырсыз аз шама, яғни 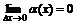 . Түрлендірейік,
. Түрлендірейік,
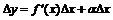 ,
,
мұндағы 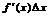 - функция өсімшесінің сызықты бөлігі деп аталады және ол
- функция өсімшесінің сызықты бөлігі деп аталады және ол 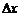 өсімшеге пропорционал. Ал
өсімшеге пропорционал. Ал 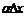 шама екі ақырсыз аздың көбейтіндісі ретінде
шама екі ақырсыз аздың көбейтіндісі ретінде 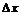 өсімшеге қарағанда жоғары ретті ақырсыз аз шама болады.
өсімшеге қарағанда жоғары ретті ақырсыз аз шама болады.
Анықтама. Функция өсімшесінің сызықты бөлігі функция дифференциалы деп аталады да, dy деп белгіленеді. Сонымен,
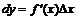
y=x функциясының дифференциалын табайық: 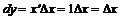 . Демек аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз:
. Демек аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз:
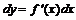 (4)
(4)
Егер аргумент өсімшесі абсолют шамасы бойынша аз шама болса, онда функция өсімшесі мен дифференциалы жуық шамамаен тең болады, яғни 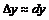 . Түрлендірейік,
. Түрлендірейік, 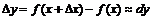 . Осыдан,
. Осыдан,
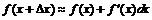 (5).
(5).
(5) формуламен функцияның мәнін жуықтап есептейді. Неғұрлым 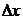 аз болса, соғұрлым формула дәлірек болады.
аз болса, соғұрлым формула дәлірек болады.
В)Дифференциалдау ережелері. u=u(x) және v=v(x) функциялардың әрқайсысы берілгенх нүктесінде дифференциалданатын болса, онда бұл функциялардың қосындысы(айырымы), көбейтіндісі және қатынасы (v(x) 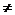 0) сол нүктеде дифференциалданады, және мына формулалар дұрыс болады:
0) сол нүктеде дифференциалданады, және мына формулалар дұрыс болады:
1) 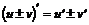
2) 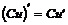 , C=const
, C=const
3) 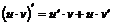
4) 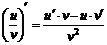 .
.
5) f(u(x)) күрделі функция туындысы:
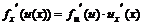 .
.
6) y=f(x) функциясына кері функция (x=f - 1(y)) туындысы:
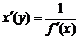 .
.
7) Айқын емес түрде берілген функция, F(x,y)=0, туындысы:
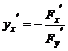 .
.
8) Дәрежелі-көрсеткіштік 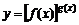 функция туындысы. Алдымен берілген теңдеудің екі жағын логарифмдейік,
функция туындысы. Алдымен берілген теңдеудің екі жағын логарифмдейік,
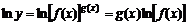 .
.
Екі жағынан туынды аламыз,
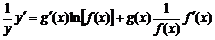 .
.
Сонымен,
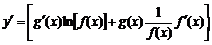
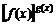 .
.
9) Жоғары ретті туынды. 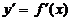 туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да,
туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да,  деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен,
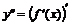 .
.
Осылайша 3-ретті, т.с.с. n–ретті туындыларды анықтауға болады,
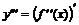 , …,
, …, 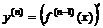 .
.
Анықтама. 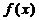 функциясы
функциясы 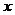 нүктесінде дифференциалданады, егер оның осы нүктеде дифференциалы болса.
нүктесінде дифференциалданады, егер оның осы нүктеде дифференциалы болса.
Егер 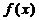 функциясы дифференциалданатын болса, онда ол міндетті түрде үзіліссіз болады.
функциясы дифференциалданатын болса, онда ол міндетті түрде үзіліссіз болады.
Дифференциалды жуықтап есептеулерге пайдалану.
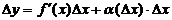
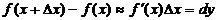
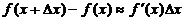 . Соңғы жуықталған теңдік ең алдымен тәжірибелік тұрғыдан қарағанда келесі есепті шешу үшін қолданады:
. Соңғы жуықталған теңдік ең алдымен тәжірибелік тұрғыдан қарағанда келесі есепті шешу үшін қолданады: 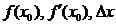 мәндері белгілі;
мәндері белгілі; 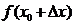 -тің жуық мәнін есептеу керек. Сонда төменгі формула анықталады:
-тің жуық мәнін есептеу керек. Сонда төменгі формула анықталады: 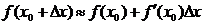 .
.
Мысалы: 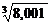 мәнін табу керек:
мәнін табу керек: 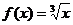 ,
, 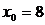 ,
, 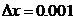 , демек
, демек 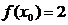 . Ал
. Ал 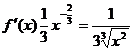 ,
, 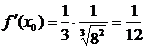 . Сонда
. Сонда 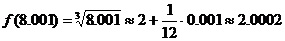 .
.
18. Анықталмаған интегралды интегралдаудың негізгі әдістері
А)Айнымалыны ауыстыру әдісін қолданып интегралдау
Айнымалыны ауыстыру әдісін қолданып интегралдау интегралға жаңа айнымалы енгізуге негізделген. Жаңа айнымалы енгізу негізінде берілген интеграл жаңа интегралға, яғни, кестелік немесе кестелік интегралға куелтірілетін интегралға көшеді. 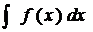 интегралын есептеу қажет болсын.
интегралын есептеу қажет болсын. 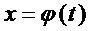 жаңа айнымалысын енгіземіз, мұндағы
жаңа айнымалысын енгіземіз, мұндағы 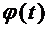 - үзіліссіз туындысы бар функция.
- үзіліссіз туындысы бар функция.  Онда
Онда 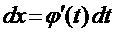 және анықталмаған интегралды интегралдаудың инварианттылық формуласының қасиеттері негізінде айнымалыны ауыстыру формуласын аламыз:
және анықталмаған интегралды интегралдаудың инварианттылық формуласының қасиеттері негізінде айнымалыны ауыстыру формуласын аламыз: 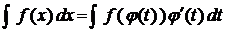
Бұл формула анықталмаған интегралда айнымалыны ауыстыру формуласы деп аталады. Интегралдың оң жағын есептеп шығарғаннан кейін интегралдың жаңа айнымалысы t –дан қайта x айнымалысына көшеміз.
Б)Бөліктеп интегралдау әдісі
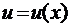 және
және 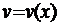 функциялары үзіліссіз туындылары бар функциялар болсын. Онда
функциялары үзіліссіз туындылары бар функциялар болсын. Онда 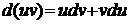 . Бұл теңдіктің екі жағын да интегралдасақ
. Бұл теңдіктің екі жағын да интегралдасақ 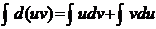 немесе
немесе 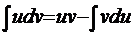
Бұл бөліктеп интегралдау формуласы деп аталады. Бұл формула берілген 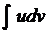 интегралынан гөрі қарапайым болатын
интегралынан гөрі қарапайым болатын 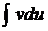 интегралына келтіреді. Бөліктеп интегралдауды мынадай түрдегі интегралдарға қолданған қолайлы:
интегралына келтіреді. Бөліктеп интегралдауды мынадай түрдегі интегралдарға қолданған қолайлы:
1. 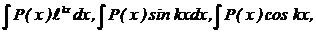 түріндегі интегралдар, мұндағы
түріндегі интегралдар, мұндағы 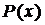 - көпмүшелік,
- көпмүшелік, 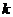 - тұрақты сан.
- тұрақты сан. 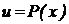 деп, ал
деп, ал 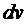 ретінде қалған интеграл астындағы көбейткіштерді алған ыңғайлы.
ретінде қалған интеграл астындағы көбейткіштерді алған ыңғайлы.
2. 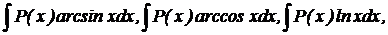
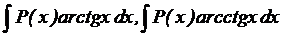 түріндегі интегралдар.
түріндегі интегралдар. 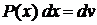 деп, ал
деп, ал 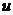 ретінде қалған интеграл астындағы көбейткіштерді алған ыңғайлы.
ретінде қалған интеграл астындағы көбейткіштерді алған ыңғайлы.
3. 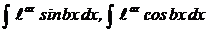 түріндегі интегралдар, мұндағы
түріндегі интегралдар, мұндағы 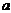 және
және 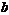 - тұрақты сандар.
- тұрақты сандар.
Мысал. 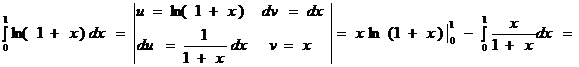
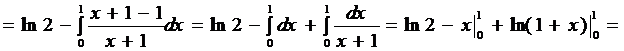
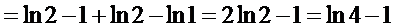
19.Екі айнымалыға тәуелді курделі функция туындысы
Егер z=f(x,y), x=x(t), y=y(t) болса, онда z=f[x(t);y(t)] болып t-ның күрделі функциясы болады. Сонда
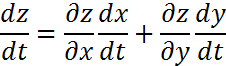
Дербес жағдайда z=(x;y),y=y(x) болса,онда
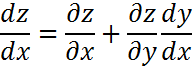
y=y(x)функциясы f (x,y)=0 айқындалмаған түрде берілсе:
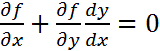 немесе y’=- f’x/f’y
немесе y’=- f’x/f’y
Егер z=f(x,y),мұндағы x=x(u;v), y=y(u;v)болса,онда
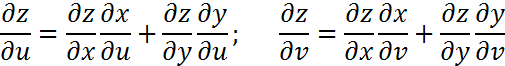
Айнымалдар саны екіден көп болған жағдайда да бұл формулалардың құрамы сақталады.
Мысалы. z=x2+xy+y2,x=t2,y=t3 болса, 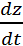 туындыны табу керек
туындыны табу керек
Шешуі: 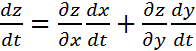 формуласы бойынша толық туынды
формуласы бойынша толық туынды
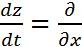 (x2+xy+y2)
(x2+xy+y2) 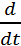 (t2)+
(t2)+ 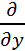 (x2+xy+y2)
(x2+xy+y2) 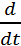 (t3)= =(2x+y)2t+(x+2y)*3t2=(2t2+t3)2t+(t2+2t3)3t2=6t5+5t4+4t3
(t3)= =(2x+y)2t+(x+2y)*3t2=(2t2+t3)2t+(t2+2t3)3t2=6t5+5t4+4t3
Толық дифференциал.Жуықтап есептеу
Егер тәуелсіз айнымалылардың 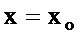 ,
, 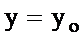 ,
, 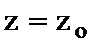 мәніне
мәніне 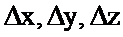 өсімшелерін берсек, онда
өсімшелерін берсек, онда 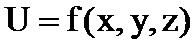 функциясы
функциясы
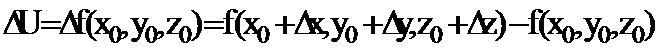
өсімшесін алады. Берілген функцияның осы өсімшесін оның толықөсімшесі деп атайды.
Теорема 1 Егер 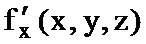 ,
, 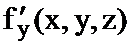 ,
, 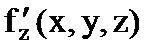 дербес туындылар
дербес туындылар 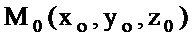 нүктесімен оның қандайда болмасын бір
нүктесімен оның қандайда болмасын бір 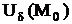 маңайында бар болып және осы нүктеде (
маңайында бар болып және осы нүктеде (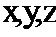 -тің функциясы ретінде) үзіліссіз болса, онда берілген
-тің функциясы ретінде) үзіліссіз болса, онда берілген 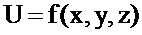 функциясының толық өсімшесі мына түрде жазылады:
функциясының толық өсімшесі мына түрде жазылады:
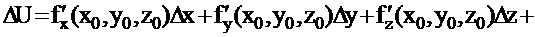
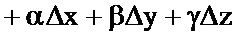 ,
,
мұндағы 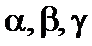 шамалары
шамалары 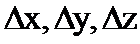 өсімшелеріне тәуелді және
өсімшелеріне тәуелді және 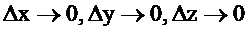 -да
-да 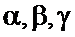 -ларда 0-ге ұмтылатын ақырсыз аз шамалар.
-ларда 0-ге ұмтылатын ақырсыз аз шамалар.
Теорема 2 Егер Q аймағында анықталған 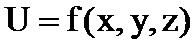 функциясының осы аймақтағы
функциясының осы аймақтағы 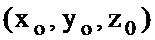 мен
мен 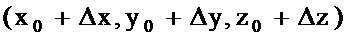 нүктелері үшін толық өсімшесі
нүктелері үшін толық өсімшесі
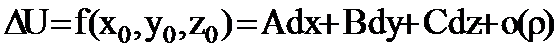
түрінде жазылатын болса (А,В,С-тұрақтылар, 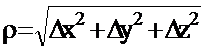 ), онда берілген функцияның
), онда берілген функцияның 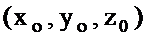 нүктесінде дербес туындылары бар болады.
нүктесінде дербес туындылары бар болады.
Анықтама Егер 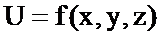 функциясының толық өсімшесі (5) немесе (6) формулаларының бірімен өрнектелетін болса, онда бұл функция
функциясының толық өсімшесі (5) немесе (6) формулаларының бірімен өрнектелетін болса, онда бұл функция 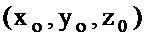 нүктесінде дифференциалданатын функция деп аталады. Сонымен бірге, берілген функцияның толық өсімшесінің сызықты бас бөлімі
нүктесінде дифференциалданатын функция деп аталады. Сонымен бірге, берілген функцияның толық өсімшесінің сызықты бас бөлімі 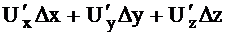 оның толықдифференциалы деп аталады да,
оның толықдифференциалы деп аталады да, 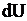 немесе
немесе 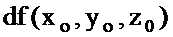 деп белгіленеді.
деп белгіленеді.
Сонымен үзіліссіз дербес туындылары бар кез келген көп айнымалды функция дифференциалданады.
Тәуелсіз 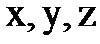 – айнымалыларының өсімшелері олардың дифференциалдары деп алынатынын ескерсек,
– айнымалыларының өсімшелері олардың дифференциалдары деп алынатынын ескерсек, 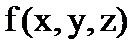 функцияның толық дифференциалы
функцияның толық дифференциалы 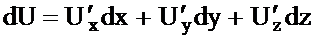 немесе
немесе
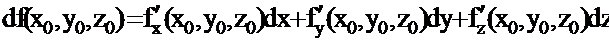
түрінде жазылады. Яғни көп аргументті функцияның толық дифференциалы оның дербес дифференциалдарының қосындысына тең.
Жуықтап есептеу. 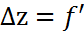 x(x,y)
x(x,y) 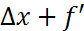 y(x;y
y(x;y 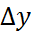 )+○(
)+○(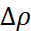 ) және df=dz=f’x(x;y)
) және df=dz=f’x(x;y) 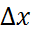 +f’y(x;y)
+f’y(x;y) 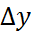 теңдіктерді салыстырғанда,
теңдіктерді салыстырғанда, 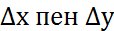 жеткілікті кіші шама болса,функцияның толық өсімшесі мен толық
жеткілікті кіші шама болса,функцияның толық өсімшесі мен толық
дифференциалы арасында жуық теңдік жазуға болады: 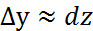 .Немесе
.Немесе
f( 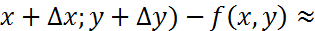 f’x(x,y)
f’x(x,y) 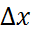 +f’y(x,y)
+f’y(x,y) 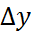
Бұдан f( 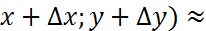 f(x,y)+f’(x,y)
f(x,y)+f’(x,y) 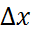 +f’y(x,y)
+f’y(x,y) 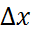
Мысал,(1,04)2,03санды жуықтап есептеу керек.
Шешуі. (1,04)2,03 саны 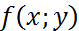 =xyфункциясының x+
=xyфункциясының x+ 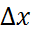 =1,04,y+
=1,04,y+ 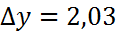 болғандағы дербес мәні х=1,
болғандағы дербес мәні х=1, 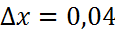 , y=2,
, y=2, 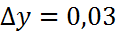 деп алсақ, f(x,y)=f(1;2)=12=1,әрі f’x(x,y)=xylnx, f’x(1,2)=2, f’y(1,2)=0 екенін ескерсек, (1,04)2,03=1+2*0,04+0*0,03=1,08.
деп алсақ, f(x,y)=f(1;2)=12=1,әрі f’x(x,y)=xylnx, f’x(1,2)=2, f’y(1,2)=0 екенін ескерсек, (1,04)2,03=1+2*0,04+0*0,03=1,08.
20. Жоғарғы ретті дербес туындылар және дифференциалдар
Туынды ұғымы. Функция өсімшесінің аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған кездегі шегі функция туындысы деп аталады. Әдетте оны 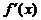 немесе
немесе 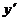 деп белгілейді:
деп белгілейді: 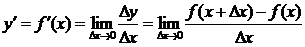 (1) Функцияның туындысын алуды – функцияны дифференциалдау дейді. (а;в) интервалының әрбір нүктесінде туындысы бар функцияны сол интервалда дифференциалданады дейді. Мынадай тұжырым дұрыс болады: Егер f(x) функцисы х0 нүктеде дифференциалданса, онда функция х0 нүктеде үзіліссіз болады. Бірақ осыған кері тұжырым дұрыс бола бермейді. Мысалы, y= | x | функциясы x=0 нүктеде үзіліссіз. Бірақ оның x=0 нүктедегі туындысы болмайды. Шынында да, егер бар болса, туындыны мына формуламен табар едік:
(1) Функцияның туындысын алуды – функцияны дифференциалдау дейді. (а;в) интервалының әрбір нүктесінде туындысы бар функцияны сол интервалда дифференциалданады дейді. Мынадай тұжырым дұрыс болады: Егер f(x) функцисы х0 нүктеде дифференциалданса, онда функция х0 нүктеде үзіліссіз болады. Бірақ осыған кері тұжырым дұрыс бола бермейді. Мысалы, y= | x | функциясы x=0 нүктеде үзіліссіз. Бірақ оның x=0 нүктедегі туындысы болмайды. Шынында да, егер бар болса, туындыны мына формуламен табар едік: 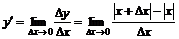 .Ал x=0 нүктеде
.Ал x=0 нүктеде 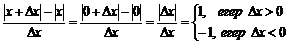 болғандықтан
болғандықтан  қатынастың шегі болмайды. Шекболмасатуындысы да жоқ.
қатынастың шегі болмайды. Шекболмасатуындысы да жоқ.
Дифференциалдау ережелері. u=u(x) және v=v(x) функциялардың әрқайсысы берілгенх нүктесінде дифференциалданатын болса, онда бұл функциялардың қосындысы(айырымы), көбейтіндісі және қатынасы (v(x) 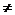 0) сол нүктеде дифференциалданады, және мына формулалар дұрыс болады:
0) сол нүктеде дифференциалданады, және мына формулалар дұрыс болады:
1) 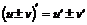
2) 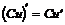 , C=const
, C=const
3) 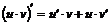
4) 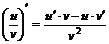 .
.
9) f(u(x)) күрделі функция туындысы: 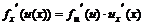 .
.
10) y=f(x) функциясынакері функция (x=f - 1(y)) туындысы: 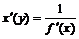 .
.
11) Айқынеместүрдеберілген функция, F(x,y)=0, туындысы: 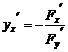 .
.
12)Дәрежелі-көрсеткіштік 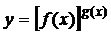 функция туындысы. Алдыменберілгентеңдеудіңекіжағын логарифмдейік,
функция туындысы. Алдыменберілгентеңдеудіңекіжағын логарифмдейік, 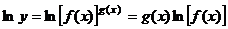 .
.
Екіжағынантуындыаламыз, 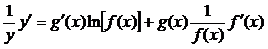 .
.
Сонымен, 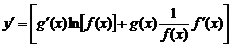
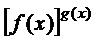 .
.
ФУНКЦИЯ ДИФФЕРЕНЦИАЛЫ. Функция шегінің анықтамасына сүйеніп туынды табу 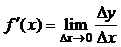 формуласын мынадай түрде көшіріп жазуға болады:
формуласын мынадай түрде көшіріп жазуға болады: 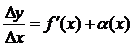 ,мұндағы
,мұндағы 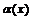 - ақырсыз аз шама, яғни
- ақырсыз аз шама, яғни 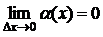 . Түрлендірейік,
. Түрлендірейік, 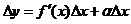 ,мұндағы
,мұндағы 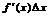 - функция өсімшесінің сызықты бөлігі деп аталады және ол
- функция өсімшесінің сызықты бөлігі деп аталады және ол 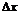 өсімшеге пропорционал. Ал
өсімшеге пропорционал. Ал 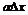 шама екі ақырсыз аздың көбейтіндісі ретінде
шама екі ақырсыз аздың көбейтіндісі ретінде 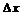 өсімшеге қарағанда жоғары ретті ақырсыз аз шама болады. Функция өсімшесінің сызықты бөлігі функция дифференциалы деп аталады да, dy деп белгіленеді. Сонымен,
өсімшеге қарағанда жоғары ретті ақырсыз аз шама болады. Функция өсімшесінің сызықты бөлігі функция дифференциалы деп аталады да, dy деп белгіленеді. Сонымен, 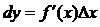 y=x функциясының дифференциалын табайық:
y=x функциясының дифференциалын табайық: 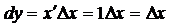 . Демек аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз:
. Демек аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз: 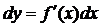 (4)
(4)
Егер аргумент өсімшесі абсолют шамасы бойынша аз шама болса, онда функция өсімшесі мен дифференциалы жуық шамамаен тең болады, яғни 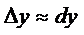 . Түрлендірейік,
. Түрлендірейік, 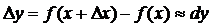 . Осыдан,
. Осыдан, 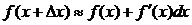 (5). (5) формуламен функцияның мәнін жуықтап есептейді. Неғұрлым
(5). (5) формуламен функцияның мәнін жуықтап есептейді. Неғұрлым 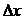 аз болса, соғұрлым формула дәлірек болады.
аз болса, соғұрлым формула дәлірек болады.
с) Жоғары ретті туынды. 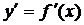 туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да,
туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да,  деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен, 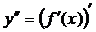 .
.
Осылайша 3-ретті, т.с.с. n–ретті туындыларды анықтауға болады, 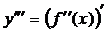 , …,
, …, 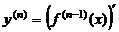 .
.
21. Екі айнымалы функцияның экстремумы
А)Функцияның өсу және кемуінің қажетті және жеткілікті шартары. Анықтама. х0 нүктесінің 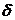 - маңайы табылып, (х0-
- маңайы табылып, (х0- 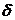 х0+
х0+ 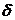 ), осы маңайдағы барлық х
), осы маңайдағы барлық х 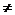 х0 үшін f(x)>f(х0) теңсіздігі орындалса, х0 нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х0) теңсіздік орындалса, х0 нүктесі f(x) функциясының максимум нүктесі деп аталады. Теорема (функция өсуі мен кемуінің жеткілікті шарты). Егер (а,в) интервалында дифференциалданатын y=f(x) функциясының туындысы оң болса, онда осы интервалда функция өспелі болады, ал туындысы теріс болса, функция кемімелі болады. 1-суреттегі y=f(x) функциясы
х0 үшін f(x)>f(х0) теңсіздігі орындалса, х0 нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х0) теңсіздік орындалса, х0 нүктесі f(x) функциясының максимум нүктесі деп аталады. Теорема (функция өсуі мен кемуінің жеткілікті шарты). Егер (а,в) интервалында дифференциалданатын y=f(x) функциясының туындысы оң болса, онда осы интервалда функция өспелі болады, ал туындысы теріс болса, функция кемімелі болады. 1-суреттегі y=f(x) функциясы 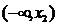 және
және 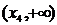 аралығында өседі,
аралығында өседі, 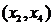 аралығында кемиді.
аралығында кемиді.
|
 2018-02-20
2018-02-20 1882
1882
 у
у