Постановка бикритериальной задачи разбиения

Пусть задан неориентированный взвешенный граф G (X, V, w, d) порядка n, где X ={ x ₁,…, x_n } – множество вершин; V Í X ´ X – множество ребер; w: V ® R ⁺– отображе­ние, определяющее вес каждого ребра; d: X ® R ⁺ – отображение, опреде­ляю­щее вес каждой вершины, где R ⁺ – множество действительных неотри­ца­тельных чисел.

Требуется определить разбиение множества вершин X графа G (X, V, w,d) на k подмножеств (X ₁, X ₂,…, X_k) таким образом, чтобы для кусков графа G ₁(X ₁, V ₁, w ₁, d ₁), G ₂(X ₂, V ₂, w ₂, d ₂), …, G_k (X_k, V_k, w_k, d_k) выполнялись требования (1).

В качестве первого критерия оптимальности F ₁, определяющего эффек­тивность k -разбиения (X ₁,…, X_k), будем рассматривать суммарный вес всех ребер, целиком попавших в один из подграфов разбиения:

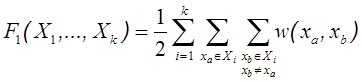
(11)

Суммарный вес вершин, принадлежащих одному подграфу, будем называть весом подграфа. Вес некоторого подграфа X_i будем обозначать через W (X_i). Для уравнивания весов получаемых подграфов будем использовать следую­щий критерий оптимальности F ₂:

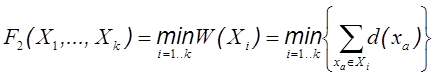
(12)

Таким образом имеем бикритериальную задачу:

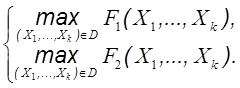
(13)

Система требований (1), предъявленных к разбие­нию (X ₁,…, X_k), опре­деля­ет область поиска D задачи k -разбиения графа. В этом случае решением экстре­маль­ной задачи (13) является Парето-область из компромиссных решений. Данная задача относится к задачам переборного типа и общее число допус­ти­мых решений | D | также можно вычислить из выражения (3).