Проверка адекватности подобранной модели имеющимся статистическим данным: графические методы

Весь рассмотренный нами комплекс процедур получения статистических выводов для линейной модели регрессии (простой или множественной) опирается на вполне определенные предположения о модели наблюдений.

В связи с этим, большие значения коэффициента детерминации  (близкие к 1) или статистическая значимость коэффициентов вовсе не обязательно говорят о том, что подобранная модель действительно хорошо соответствует характеру статистических данных (адекватна статистическим данным).

В этом отношении весьма поучителен искусственный пример с четырьмя различными множествами данных, которые имеют качественно различные диаграммы рассеяния и в то же время приводят при использовании модели наблюдений

к одним и тем же (в пределах двух знаков после запятой) оценкам параметров, значениям коэффициента и - статистик. Эти множества данных приведены в следующей таблице.

	Множество 1		Множество 2		Множество 3		Множество 4
i	x	y	x	y	x	y	x	y
1	20	16.06	20	18.28	20	14.92	16	13.16
2	16	13.90	16	16.28	16	13.54	16	11.52
3	26	15.16	26	17.48	26	25.48	16	15.42
4	18	17.62	18	17.54	18	14.22	16	17.68
5	22	16.66	22	18.52	22	15.62	16	17.94
6	28	19.92	28	16.20	28	17.68	16	14.08
7	12	14.48	12	12.26	12	12.16	16	10.50
8	8	8.52	8	6.20	8	10.78	38	25.00
9	24	21.68	24	18.26	24	16.30	16	11.12
10	14	9.64	14	14.52	14	12.84	16	15.82
11	10	11.36	10	9.48	10	11.46	16	17.98

Для всех четырех множеств

подобранная модель линейной связи имеет вид ,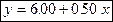

 имеет (оцененную) стандартную ошибку

 имеет (оцененную) стандартную ошибку

-статистика для проверки нулевой гипотезы 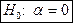 равна 2.67, что соответствует -значению 0.026,

-статистика для проверки нулевой гипотезы  равна 4.24, что соответствует -значению 0.002,

.

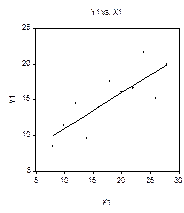
Однако диаграммы рассеяния различаются коренным образом:

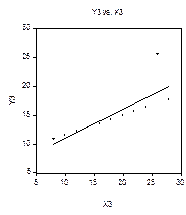
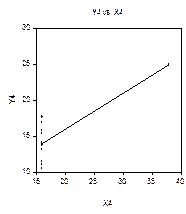
Уже чисто визуальный анализ четырех диаграмм рассеяния показывает, что

только первое множество данных можно признать удовлетворительно описываемым линейной моделью наблюдений

Для второго множества более подходящей представляется модель

В третьем множестве выделяется одна точка (3-е наблюдение), которая существенно влияет на наклон и положение подбираемой прямой.

Четвертое множество совершенно непригодно для подбора линейной зависимости, поскольку подобранная прямая фактически определяется наличием одного выпадающего наблюдения

Метод наименьших квадратов достаточно устойчив к малым отклонениям от стандартных предположений, в том смысле, что при таких малых отклонениях статистические выводы на основе анализа модели в основном сохраняются. Однако существенные отклонения от стандартных предположений могут серьезно исказить выводы на основе статистического анализа модели. В связи с этим необходимо

иметь возможность обнаружения отклонений от стандартных предположений,

иметь инструментарий для коррекции выявленных отклонений от стандартных предположений, позволяющий проводить строгий и информативный анализ статистических данных.

Эффективным средством обнаружения отклонений от стандартных предположений о линейной модели наблюдений

является анализ остатков, т. е. анализ разностей

Наблюдаемые разности  мы, в силу случайности значений  в модели наблюдений, можем рассматривать как значения соответствующих случайных величин , за которыми сохраним те же обозначения .

Если выполнены наши стандартные предположения о модели наблюдений, то остатки , рассматриваемые как случайные величины , имеют нулевые математические ожидания

и дисперсии

где  — -й диагональный элемент квадратной -матрицы

Таким образом, несмотря на то, что дисперсии ошибок   равны между собой при наших предположениях (все они равны 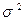), дисперсии остатков, вообще говоря, различны.

Для выравнивания дисперсий можно перейти к рассмотрению нормированных остатков

для которых

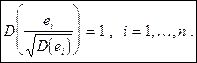
Поскольку значение 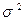 опять не известно, вместо нормированных остатков приходится использовать «стьюдентизированные» остатки

где, как обычно, .

Во многих пакетах программ величины  в знаменателе правой части выражения для   игнорируются, что приводит к так называемым «стандартизованным» остаткам

так сделано, например, в пакете EXCEL. Практический анализ показывает, что графики остатков  и  обычно мало отличаются по характеру поведения. Поэтому для предварительного графического анализа адекватности вполне можно удовлетвориться значениями . К тому же, можно показать, что

(  — количество объясняющих переменных), так что если  (  много меньше ), то «в среднем» значения  достаточно малы.

Графики стандартизованных (стьюдентизированных) остатков позволяют выявлять типичные отклонения от стандартных предположений о модели наблюдений по характеру поведения остатков. При этом имеется в виду, что, по крайней мере при большом количестве наблюдений, поведение остатков , должно имитировать поведение ошибок . Иначе говоря, поскольку мы предполагаем, что ошибки  — независимые в совокупности случайные величины, имеющие одинаковое нормальное распределение 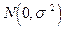, то ожидаем, что поведение последовательности остатков  должно имитировать поведение последовательности независимых в совокупности случайных величин, имеющих одинаковое нормальное распределение 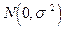. Соответственно, от стандартизованных остатков можно было бы ожидать поведения, похожего на поведение последовательности независимых в совокупности случайных величин, имеющих одинаковое стандартное нормальное распределение .

Строго говоря, последнее ожидание не вполне верно. Именно, хотя стандартизованные остатки и имеют распределения, близкие (хотя бы при больших ) к стандартному нормальному, они не являются взаимно независимыми случайными величинами. Это можно понять хотя бы из того, что (как мы помним) при использовании оценок наименьших квадратов алгебраическая сумма остатков равна нулю, так что каждый остаток линейно выражается через остальные остатки. Тем не менее при большом количестве наблюдений наличие такого соотношения между остатками практически не делает картину поведения стандартизованных остатков сколь-нибудь существенно отличной от поведения последовательности независимых в совокупности случайных величин, имеющих одинаковое стандартное нормальное распределение .

Наиболее часто для диагностики (проверки на наличие) типичных отклонений используют графики зависимости стандартизованных остатков (как ординат) от

оцененных значений ;

отдельных объясняющих переменных;

номера наблюдения, если наблюдения производятся в последовательные моменты времени с равными интервалами.

График зависимости   от  позволяет выявлять три довольно распространенных дефекта модели:

Выделяющиеся наблюдения (outliers) — наличие отдельных наблюдений, для которых либо математическое ожидание ошибки  существенно отличается от нуля либо дисперсия ошибки 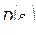 существенно превышает величину  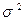дисперсий остальных ошибок. Подобные наблюдения могут обнаруживать себя на указанном графике как наблюдения со «слишком большими» по абсолютной величине остатками. Такая ситуация возникает, например, при подборе прямой по третьему (из четырех рассматривавшихся выше) множеству данных:

Неоднородность дисперсий (heteroscedasticity), например, в форме той или иной функциональной зависимости 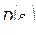 от величины 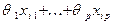. Так, если рассматриваемый график имеет вид

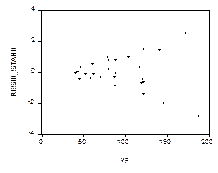
то это скорее всего отражает возрастание дисперсий ошибок с ростом значений .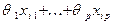

Неправильная спецификация модели в отношении множества объясняющих переменных, приводящая к нарушению соотношения , так что . Такая ситуация возникает, например, при оценивании второго множества данных из четырех рассматривавшихся выше:

График зависимости   от значений -й объясняющей переменной полезен для выявления нелинейной зависимости   от -й объясняющей переменной. Например, для второго из четырех искусственных множеств данных имеем

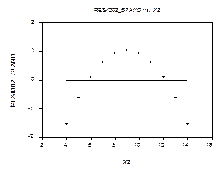
График зависимости остатков от номера наблюдения полезен в случае, когда наблюдения производятся последовательно во времени (через равные интервалы времени). По такому графику можно обнаружить