Элементы электрической цепи переменного тока

В таблице 2.2 приведены пассивные элементы, их изображения и обозначения, формы записи сопротивления и проводимости.

Таблица 2.2

Наименова-ние элемента	Свойства элемента	Изображе-ние и буквенное обозначение	Сопротив-ление при синусоид. токе	Запись сопротив-ления в комплекс-ной форме	Проводи- мость при синусои-дальном токе	Запись проводи-мости в комп-лексной форме
Резистор	Эл. соп-ротивле-ние	R	R	R	g = 1/R	g = 1/R
Индуктив-ная катушка	Индук-тивность	L	xL=wL	Z L= jwL	bL=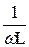	Y L=1/ Z L= = – jbL
Конденса-тор	Емкость	C	xC =1/wC	Z C= –j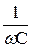	bC = wC	Y C=1/ Z C= = jbC

Законы Ома и Кирхгофа в комплексной форме записи.

Закон Ома:

,

где Z – комплексное сопротивление участка цепи.

Например, для изображенной на рис. 2.4. цепи, комплексное сопротивление равно Z = R+j(x_L – x_C).

Рис. 2.4. Цепь с активно-индуктивно-емкостной нагрузкой

 

Первый закон Кирхгофа для мгновенных и комплексных токов соответственно:

; .

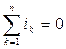Второй закон Кирхгофа для мгновенных и комплексных напряжений и э.д.с. соответственно:

; .

 

Последовательное и параллельное соединение сопротивлений и проводимостей.

На рисунках 2.5 и 2.6 изображены соответственно последовательная и параллельная электрические цепи.

При последовательном соединении общее сопротивление цепи равно

.

При параллельном соединении общая проводимость цепи равна

.

Формулы для преобразования последовательной цепи в параллельную и для выполнения обратного преобразования имеют вид:

Y = =  = g – jb;       g =  ; b = ;

Z = = R + jX; R =  ; X = .

(здесь g и b – соответственно активная и реактивная проводимости; R и X – активное и реактивное сопротивления).

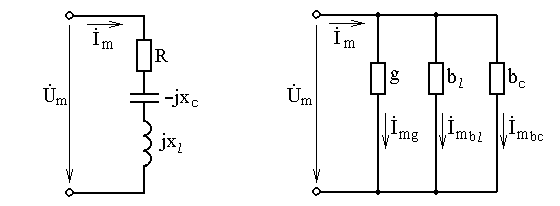
  Рис. 2.5. Последовательное              Рис. 2.6. Параллельное соединение

   соединение сопротивлений                             проводимостей

 

Необходимо помнить, что взаимообратными являются лишь комплексы Z и Y, а их составляющие R и g, Х и b не являются таковыми.