Алгоритм великого та малого кроку

Примітивний алгоритм

Для знаходження log_g b (g – генератор G порядка n, b Î G) будемо обчислювати значення g, g ², g ³, g ⁴,... поки не отримаємо b. Часова оцінка алгоритму – O(n). Якщо n – велике число, то час обчислення логарифму є достатньо великим і тому алгоритм є неефективним.

Алгоритм великого та малого кроку

Першим детермінованим алгоритмом для обчислення дискретного логарифму був алгоритм великого та малого кроку, запропонований Шанком (Shank) [1].

Для обчислення log _gb в групі Z_n ^* необхідно зробити наступні кроки:

1. Обчислити a = é 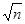ù;

2. Побудувати список L₁ = 1, g^a, g ² ^a,..., g (за модулем n);

3. Побудувати список L₂ = b, bg, bg ²,..., bg^a ^{- 1} (за модулем n);

4. Знайти число z, яке зустрілося в L₁ та L₂.

Тоді z = bg^k = g^la для деяких k та l. Звідси b = g^la^-^k = g^x; x = la - k.

Два питання постає при дослідженні роботи наведеного алгоритму:

1. Чи завжди знайдеться число, яке буде присутнім в обох списках?

2. Як ефективно знайти значення z?

Запишемо x = sa + t для деяких s, t таких що 0 £ s, t < a. Тоді b = g^x = g^s^a ⁺^t. Домножимо рівність на g^a ^- ^t, отримаємо: bg^a ^-^t = g^s ⁽ ^a ^{+ 1)}. Значення зліва обов’язково зустрінеться в L₂, а справа – в L₁.

Відсортуємо отримані списки L₁ та L₂ за час O(a * log a). За лінійний час проглядаємо списки зліва направо порівнюючи їх голови: якщо вони рівні, то значення z знайдене, якщо ні – то видалити менше число і продовжити перевірку.

Приклад. Розв’язати рівняння: 2^x º 11 (mod 13).

a = é ù = 4;

L₁: 1, 2⁴ º 3, 2⁸ º 9, 2¹² º 1, 2¹⁶ º 3;

L₂: 11, 11 * 2 º 9, 11 * 2² º 5, 11 * 2³ º 10;

Число 9 зустрілося в обох списках. 11 * 2 º 2⁸, 11 º 2⁷, звідки x = 7.

Відповідь: x = 7.

Інший підхід до реалізації алгоритму великого та малого кроку можна отримати якщо рівність b = g^s^a ⁺ ^t (a = é 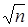ù, 0 £ s, t < a) переписати у вигляді b * (g^- ^a) ^s = g^t. Обчислимо g ^- ^a та складемо таблицю значень g^t, 0 £ t < a. Далі починаємо знаходити значення b * (g^- ^a) ^s, s = 0, 1, … перевіряючи їх наявність у таблиці g^t. Як тільки знаходяться такі s та t, алгоритм зупиняється.

Приклад. Обчислити log₂3 в групі Z₁₉^*.

3 = 2^x = 2 ^sa ⁺¹, 3 * (2^{- a}) ^s = 2 ^t. Складемо таблицю 2 ^t, 0 £ t < é ù = 5:

t	0	1	2	3	4
2^t	1	2	4	8	16

2^-1 º 10 (mod 19), оскільки 2 * 10 º 1 (mod 19).

Тоді 3 * (2^-⁵) ^s (mod 19) º 3 * (10⁵)^s (mod 19) º 3 * 3 ^s (mod 19)

Обчислюємо 3 * 3 ^s, s = 0, 1, …:

s	0	1	2
3 * 3 ^s	3	9	8

Значення 8, яке отримали при s = 2, присутнє в таблиці 2 ^t, 0 £ t < 5.

Звідси 3 * (2^-⁵)² = 2³ або 3 = (2⁵)² * 2³ = 2^5*2+3 = 2¹³.

Відповідь: 3 = 2¹³, тобто log₂3 = 13.

Алгоритм Полард - ро

Нехай G – циклічна група з порядком n (n – просте). Розіб’ємо елементи групи G на три підмножини S₁, S₂ та S₃, які мають приблизно однакову потужність. При цьому необхідне виконання умови: 1 Ï S₂. Визначимо послідовність елементів x _i наступним чином:

x ₀ = 1, x _i+1 = , i ³ 0 (1)

Ця послідовність у свою чергу утворить дві послідовності c _i та d _i, що задовольняють умові

x _i =

та визначаються наступним чином:

с ₀ = 0, с _i₊₁ = , i ³ 0 (2)

та

d ₀ = 0, d _i+1 = , i ³ 0 (3)

Алгоритм буде працювати циклічно шукаючи таке знчення i, для якого x _i = x ₂_i. Для таких значень будуть мати місце рівність = або = . Логарифмуючи останню рівність за основою a, матимемо:

(d _i - d _2i) * log _ab º (c _2i - c _i) mod n

Якщо d _i ¹ d ₂_i (mod n), то це рівняння може бути ефективно розв’язано для обчислення log _ab.

Алгоритм

Вхід: генератор a циклічної групи G з порядком n та елемент b Î G.

Вихід: дискретний логарифм x = log _ab.

1. x₀ 1, c ₀ 0, d ₀ 0.

2. for i = 1, 2,... do

2.1. За значеннями x_i _-1, c_i _-1, d_i _-1 та x ₂ _i _-2, c ₂ _i _-2, d ₂ _i _-2 обчислити значення x_i, c_i, d_i та x ₂ _i, c ₂ _i, d ₂ _i використовуючи формули (1), (2), (3).

2.2. if (x _i = x ₂_i) then

r (d_i - d ₂ _i) mod n;

if (r = 0) then return (FALSE); // розв’язку не знайдено

x r ^-1 (c_i - c ₂ _i) mod n.

return (x).

Якщо алгоритм завершується невдачею (повертає FALSE), то можна запустити його вибравши інші початкові значення c ₀, d ₀ з інтервалу [1; n - 1] та поклавши x₀ = .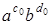

Приклад. Обчислити log₂9 в групі Z₁₉^*.

Побудуємо наступну таблицю значень послідовностей x_i, c_i, d_i:

i	x_i	a_i	b_i	x _{2 i}	a _{2 i}	b ₂ _i
1	9	0	1	18	1	1
2	18	1	1	4	4	2
3	17	2	1	4	8	6
4	4	4	2	4	16	14
5	17	4	3	4	32	30
6	4	8	6	4	64	62

На 6 кроці отримали x₆ = x₁₂. Підставивши їх значення, отримаємо:

2⁸ * 9⁶ = 2⁶⁴ * 9⁶² або 2^{8 – 64} = 9^{62 – 6}, 2^-56 = 9⁵⁶

Логарифмуємо рівність: -56 * log₂9 = 56 (mod 18), оскільки |Z₁₉^*| = 18.

Враховуючи що -56 (mod 18) º 16, 56 (mod 18) º 2, перепишемо рівність у вигляді 16 * log₂9 = 2 (mod 18) або 8 * log₂9 = 1 (mod 9). log₂9 = 8^-1 (mod 9) = 8.

Відповідь: log₂9 = 8.

Індексний алгоритм

Алгоритм, базований на обчисленні індексів, є найпотужним при обчисленні дискретного логарифму. Необхідно побудувати відносно невелику підмножину S елементів групи G, яка називається множниковою основою. Ця підмножина повинна обиратися таким чином, щоб як можна більша частина елементів G могла бути представлена у вигляді добутку її елементів. При обчисленні значення log _ab (a – генератор G, b Î G) спочатку обчислюються значення логарифмів елементів з S (які заносяться в тимчасову базу даних), а потім на їх основі обчислюється логарифм числа b.

Алгоритм

Вхід: генератор a циклічної групи G порядка n та елемент b Î G.

Вихід: дискретний логарифм x = log _ab.

1. Побудувати множину S – множникову основу. Нехай S = { p ₁, p ₂, …, p_t }. В якості значень p_i можна обрати, наприклад, i - те просте число.

2. Побудувати систему лінійних рівнянь, розв’язком якої будуть значення log _a p_i. Для цього виконаємо наступні кроки:

2.1. Обрати деяке ціле k, 0 £ k £ n - 1 та обчислити a^k.

2.2. Спробувати представити значення a^k у вигляді добутку чисел з S:

a^k = , c_i ³ 0

Якщо така рівність знайдена, то записати рівняння:

k = (mod n)

2.3. Повторювати кроки 2.1. та 2.2. поки не отримаємо t + c лінійних рівнянь. Невелике ціле число c (1 £ c £ 10) обирається таким чином, щоб складена система рівнянь мала єдиний розв’язок з великою ймовірністю (якщо скласти лише t рівнянь з t невідомими, то з великою ймовірністю два з цих рівнянь будуть залежними і тоді система буде мати більше одного розв’язку).

3. Розв’язати утворену систему рівнянь, отримати значення log _ap_i, 1£ i £ t.

4. Обчислення log _ab.

4.1. Обрати деяке ціле k, 0 £ k £ n - 1 та обчислити b * a^k.

4.2. Спробувати представити значення b * a^k у вигляді добутку чисел з S:

b * a ^k = , d_i ³ 0

Якщо такого представлення знайти не вдається, виконати знову 4.1. Інакше прологарифмірувавши останню рівність, отримаємо:

x = log _ab = ( - k) mod n

Приклад. Обчислити log₂12 в групі Z₁₉^*.

1. Нехай S = {2, 3, 5} – множникова основа.

2. Будуємо систему рівнянь для знаходження значень log₂ p_i, де p_i Î S. Оскільки множина S містить 3 елементи, то достатньо отримати 3 лінійно незалежні рівняння.