A.A. Слепышев
Исследование динамических эффектов в придонном слое море имеет актуальное значение в связи с изученим тепло-массоперноса через придонный слой, процессов седиментации и осадконакопления, генерации и эволюции донных рифелей и мезоформ, транспорта наносов и взвеси. Важный вклад в динамику придонного слоя вносят волновые процессы на шельфе и континентальном склоне. Ветровое волнение является важным фактором аккумуляции или размыва наносов непосредственно в прибрежной зоне моря [1,2]. Влияние поверхностных волн прослеживается, по-видимому, до глубин, составляющих половину длины волны [3]. На больших глубинах преобладает влияние внутренних волн и топографических волн. Нелинейные эффекты при распространении как поверхностных, так и внутренних волн проявляются в генерации средних на временном масштабе волны течений, которые обусловлены действием в слабонелинейном пакете волновых напряжений [4,5,6] В предельном случае слабонелинейной плоской волны указанные волновые напряжения отличны от 0 при учёте турбулентной вязкости и диффузии [6,7]. В придонном слое моря на шельфе и континетальном склоне существует важный класс захваченных топографических волн, физической причиной существования которых является взаимодействие гравитации и сил плавучести, с одной стороны, неодородностей рельефа дна и вращения Земли-с другой.Частота захваченных волн не превышает N 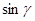 (
(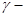 угол наклона дна). Фаза волны распространяется, оставляя более мелкую воду справа в Северном полушарии [8] Амплитуда волны затухает по экспоненциальному закону при удалении от дна. Придонные волны, по видимому, вносят важный вклад в транспорт наносов на шельфе.
угол наклона дна). Фаза волны распространяется, оставляя более мелкую воду справа в Северном полушарии [8] Амплитуда волны затухает по экспоненциальному закону при удалении от дна. Придонные волны, по видимому, вносят важный вклад в транспорт наносов на шельфе.
Если турбулентные тангенциальные напряжения у дна превышают критические значения, соответствующие началу движения наносов, волна взмучивает донный осадочный материал, осуществляя его горизонтальный перенос средними течениями, индуцированными придонными топографическими волнами.
В этой связи актуальным является определение средних течений, индуцированных придонными волнами за счёт нелинейных эффектов в присутствии турбулентной вязкости и диффузии над склоном произвольной ориентации. Исходные нелинейные уравнения гидродинамики для волновых возмущений решаются в слабонелинейном приближении методом возмущений [ 4 ]: в первом порядке малости по амплитуде волны находятся решения линейного приближения и дисперсионное соотношение, во втором порядке малости - средние течения, индуцированные волнами после осреднения исходных уравнений по периоду волны.
Горизонтальным дном будем называть плоскость, перпендикулярную вектору ускорения свободного падения и параллельную свободной невозмущённой поверхности океана. Плоскость, касательную поверхности Земли и параллельную горизонтальному дну обозначим К. Плоскость К1  , соответствующую наклонному дну, получаем из плоскости K поворотом её на угол
, соответствующую наклонному дну, получаем из плоскости K поворотом её на угол 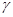 вокруг линии пересечения плоскостей К и К1 (оси Х). Условимся, что положительному значению угла
вокруг линии пересечения плоскостей К и К1 (оси Х). Условимся, что положительному значению угла 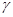 соответствует поворот плоскости K против часовой стрелки (если смотреть с положительной полуоси Х). Систему уравнений гидродинамики для волновых возмущений в приближении Буссинеска запишем в системе координат, плоскость XOY которой совпадает с плоскостью К1,ось Х совпадает с линией пересечения плоскостей K и К1 и составляет с западным направлением угол
соответствует поворот плоскости K против часовой стрелки (если смотреть с положительной полуоси Х). Систему уравнений гидродинамики для волновых возмущений в приближении Буссинеска запишем в системе координат, плоскость XOY которой совпадает с плоскостью К1,ось Х совпадает с линией пересечения плоскостей K и К1 и составляет с западным направлением угол 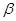 , ось Z направлена от поверхности Земли перпендикулярно плоскости К1. Положительному значению угла
, ось Z направлена от поверхности Земли перпендикулярно плоскости К1. Положительному значению угла 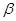
 соответствует поворот параллели к оси Х против часовой стрелки.
соответствует поворот параллели к оси Х против часовой стрелки.
Вектор угловой скорости вращения Земли имеет проекции на оси Z,Y и X соответственно
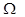 z=
z= 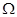
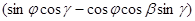 ;
; 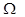 y=
y= 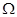 (
(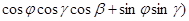 (1)
(1)
и 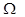 x=
x= 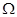
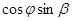
где  с-1 -угловая скорость вращения Земли,
с-1 -угловая скорость вращения Земли, 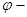 .широта.
.широта.
Турбулентные напряжения в данной работе параметризуются через сдвиги волновых скоростей по гипотезе Сент-Гелли с введением коэффициентов горизонтальной и вертикальной турбулентной вязкости и диффузии [6] Введём безразмерные переменные 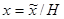 ,
,  ,
, 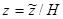 (
(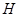 -характерная глубина),
-характерная глубина), 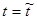
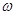 * (
* (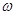 * - характерная частота волны), размерные величины отмечены волнистой чертой сверху. Определим безразмерные величины компонент волновых возмущений скорости (
* - характерная частота волны), размерные величины отмечены волнистой чертой сверху. Определим безразмерные величины компонент волновых возмущений скорости (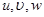 ), давления
), давления 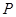 , плотности
, плотности 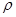 , коэффициентов вертикальнoй
, коэффициентов вертикальнoй 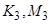 и горизонтальной
и горизонтальной 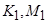 турбулентной вязкости и диффузии следующим образом:
турбулентной вязкости и диффузии следующим образом:
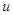 =
=  /(
/(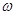 *H),
*H), 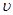 =
= 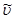 /(
/(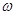 *H),
*H), 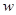 =
= 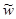 /(
/(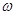 *H),
*H), 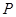 =
= 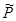 /(
/(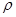 01(
01(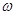 *H)2) (2)
*H)2) (2)
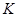 3=
3= 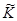 3/
3/ 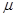 ,
, 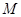 3=
3= 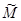 3/
3/ 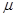 ,
, 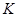 1=
1= 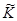 1/
1/ 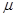 ,
, 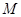 1=
1= 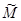 1/
1/ 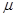 ,
, 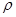 =
= 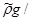 (
(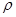 01H
01H 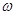 *2)
*2)
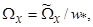
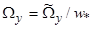
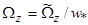
где 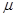 =
= 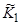 - значение горизонтальной турбулентной вязкости,
- значение горизонтальной турбулентной вязкости, 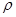 01-характерная средняя плотность воды. Система уравнений гидродинамики для волновых возмущений в безразмерных переменных в приближении Буссинеска имеет вид:
01-характерная средняя плотность воды. Система уравнений гидродинамики для волновых возмущений в безразмерных переменных в приближении Буссинеска имеет вид:
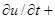 2(
2(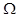 y
y 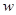 -
- 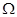 zv)+(
zv)+(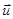
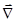
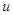 )=-
)=- 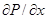
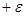 2(K1
2(K1 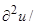
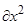 +K1
+K1 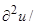
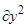 + K3
+ K3 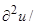
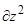 )
)
(3a)
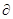
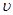 /
/ 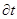 +2(
+2(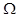 z
z 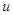 -
- 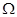 x
x 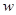 )+(
)+(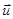
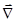
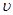 )= -
)= - 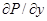 -
- 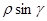 +
+ 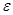 2(K1
2(K1 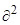
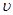 /
/ 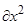 + K1
+ K1 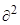
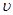 /
/ 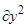 + K3
+ K3 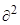
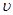 /
/ 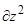 )
)
(3б)
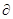
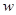 /
/ 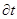 +2(
+2(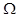 xv-
xv- 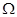 y
y 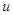 )+(
)+(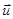
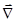
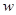 )= -
)= - 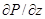 +
+ 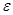 2(K1
2(K1 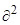
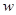 /
/ 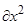 + K1
+ K1 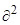 w/
w/ 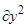 + K3
+ K3 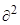
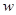 /
/ 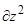 )-
)- 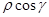 (3в)
(3в) 
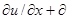
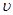 /
/ 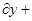
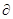
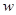 /
/ 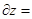 0 (3г)
0 (3г)
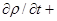 (
(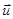
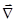
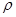 )+v
)+v 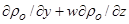 =
= 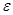 2(M1
2(M1 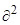
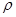 /
/ 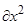 + M1
+ M1 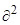
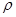 /
/ 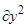 + M3
+ M3 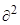
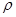 /
/ 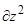 ) (3д)
) (3д)
где 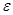 2=
2= 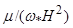 ,
, 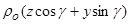 - средняя плотность,
- средняя плотность, 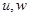 ,
, 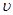 -волновые возмущения скорости течения вдоль осей X,Z,Y соответственно;
-волновые возмущения скорости течения вдоль осей X,Z,Y соответственно; 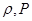 -волновые возмущения плотности и давления. Оператор (
-волновые возмущения плотности и давления. Оператор (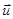
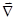 ) раскрывается по формуле: (
) раскрывается по формуле: (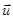
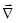 )=
)= 

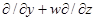

Введём частоту Брента-Вяйсяля: N2=-d 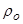 /dz1, где d
/dz1, где d 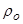 /dz1 - градиент средней плотности, z1=
/dz1 - градиент средней плотности, z1= 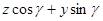 . Очевидно, что вектор градиента средней плотности коллинеарен вектору g.
. Очевидно, что вектор градиента средней плотности коллинеарен вектору g.
Уравнение (3д) можно переписать в виде:
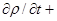 (
(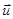
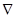 )
) 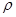 -
- 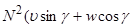 )
)  =
= 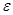 2(M1
2(M1 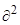
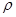 /
/ 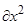 +M1
+M1 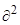
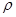 /
/ 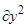 +M3
+M3 
 /
/ 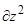 ) (4)
) (4)
Граничные условия у дна:
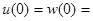
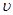 (0)=0
(0)=0
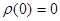 (5)
(5)
В качестве решения в линейном приближении рассмотрим волну, у которой 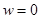 , введём функцию тока
, введём функцию тока 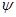 . Волновые возмущения скорости выражаются через функцию тока:
. Волновые возмущения скорости выражаются через функцию тока:

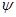 /
/ 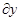
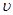 = -
= - 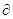
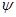 /
/ 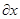 (6)
(6)
Решение системы (3) в линейном приближении будем искать в виде:
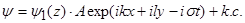
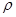
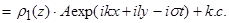 (7)
(7)
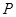
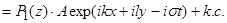
где 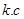 - комплексно сопряжённые слагаемые, А(
- комплексно сопряжённые слагаемые, А( -амплитудная функция, медленно меняющаяся на масштабе волны. Из системы (3) следуют уравнения для
-амплитудная функция, медленно меняющаяся на масштабе волны. Из системы (3) следуют уравнения для
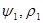 .
.
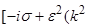
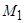 +
+ 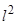
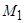 -
- 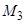 d2/d
d2/d 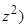 ]
] 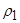 =-
=- 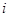
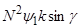 (8)
(8)
[ 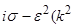
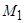 + l 2
+ l 2 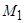 -
- 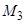 d2/d
d2/d 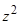 )][2
)][2 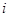
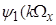 +
+ 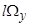 )]=
)]= 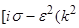
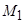 +
+ 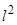
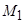 -
- 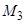 d2/d
d2/d 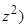 ]d/d
]d/d 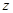 {[
{[ 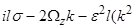
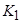 +
+ 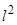
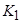 -
- 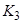 d2/d
d2/d 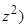 ]
] 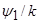 }+N2
}+N2 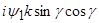
(9)
Граничные условия у дна функций 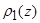 и
и 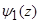 имеют вид:
имеют вид:
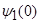 =0,
=0, 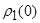 =0 (10)
=0 (10)
В [12], следуя асимптотическому методу Люстерника-Вишика [13,14],функ-
ции  (z) и
(z) и 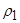 (z) и частота волны
(z) и частота волны 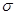 получены в виде:
получены в виде:
 (z)=
(z)= 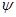 10(z)+
10(z)+ 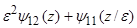
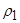 (z)=
(z)= 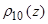 +
+ 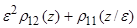 (11)
(11)
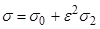
где 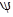 10(z) и
10(z) и 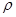 10(z) - "невязкие" решения, т.е. решения при
10(z) - "невязкие" решения, т.е. решения при 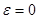 ,
, 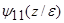 и
и 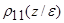 - "погранслойные" решения, быстро убывающие (по сравнению с
- "погранслойные" решения, быстро убывающие (по сравнению с 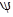 10(z)) при удалении от дна. Приведём выражения для
10(z)) при удалении от дна. Приведём выражения для 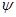 10(z)
10(z) 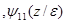 и
и  10(z)
10(z) 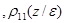 которые потребуются в дальнейшем:
которые потребуются в дальнейшем:
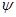 10(z)= exp(
10(z)= exp(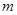 z) ,
z) , 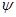 11(
11(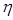 )=-exp(
)=-exp(
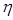 )
)
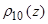 =
= 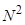
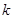 sin
sin  .
. 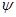 10(z)/
10(z)/ 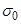 ,
,
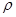 11(z)=exp(
11(z)=exp(
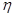 )
) 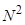
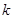 sin
sin  /
/ 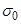 (12)
(12)
где  -дисперсионное соотношение при отсутствии турбулентной вязкости и диффузии,
-дисперсионное соотношение при отсутствии турбулентной вязкости и диффузии, 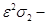 поправка к чаcтоте, обусловленная турбулентной вязкостью и диффузией [12],
поправка к чаcтоте, обусловленная турбулентной вязкостью и диффузией [12],
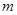 =[2
=[2 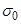
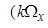 +
+ 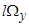 )
)  +i0.5
+i0.5 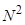
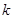 sin2
sin2  ]/[2i
]/[2i  ]
]
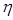 =z/
=z/ 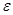 ,
, 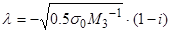 (13а)
(13а)
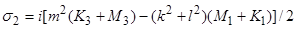 (13б)
(13б)
Амплитудная функция А 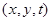 является медленно меняющейся функцией на масштабах волны. Умножим обе части уравнения (3а) на
является медленно меняющейся функцией на масштабах волны. Умножим обе части уравнения (3а) на 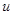 , уравнения (3б) на
, уравнения (3б) на 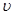 и сложим эти уравнения, после осреднения по периоду волны в линейном приближении получим уравнение для огибающей А
и сложим эти уравнения, после осреднения по периоду волны в линейном приближении получим уравнение для огибающей А 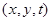 :
:
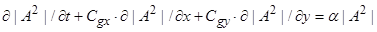 (14)
(14)
где 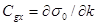 +
+ 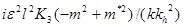 ,
,
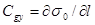 +
+ 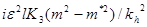 - (15)
- (15)
компонеты групповой скорости вдоль осей X и Y соответственно. 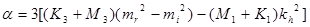
здесь 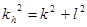 ,
, 
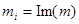
В стационарном случае уравнение (14) преобразуется к виду:
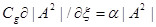 , (16)
, (16)
где  -координата вдоль луча,
-координата вдоль луча,  -групповая скорость.
-групповая скорость.
Пространственные производные функции 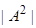 следующим образом выражаются через градиент
следующим образом выражаются через градиент 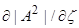
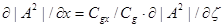 (17)
(17)
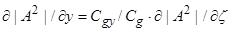
 Осредним исходные уравнения движения (3) по периоду волны, получим с точностью до членов, квадратичных по амплитуде волны уравнения для средних полей, индуцированных волной в слабонелинейном приближении (черта сверху означает осреднение по периоду волны):
Осредним исходные уравнения движения (3) по периоду волны, получим с точностью до членов, квадратичных по амплитуде волны уравнения для средних полей, индуцированных волной в слабонелинейном приближении (черта сверху означает осреднение по периоду волны):
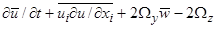
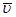 =
= 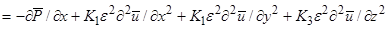
(18a)
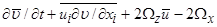
 =
= 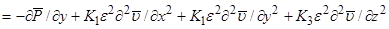
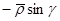
(18б)
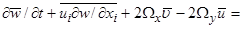
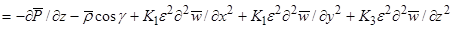 (18в)
(18в)
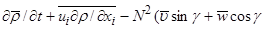 )
) 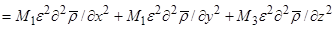 (18г)
(18г)
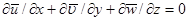 (18д)
(18д)
Волновые напряжения 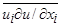 ,
, 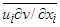 ,
, 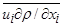 выражаются с помощью (
выражаются с помощью ( 6,7) через
6,7) через 

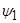 :
:
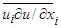
 =
= 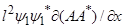 -
- 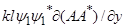
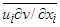 =
= 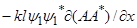 +
+ 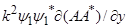 (19)
(19)
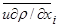 =
= 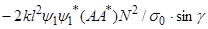
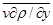 =
= 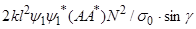
Из анализа системы (18) с учётом (19) следует, что индуцируемые волной средние поля плотности 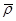 , давления
, давления 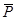 и скорости течения
и скорости течения 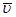 следует искать в виде:
следует искать в виде:
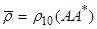 ,
, 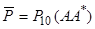 , (20)
, (20) 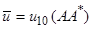 ,
, 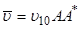 ,
, 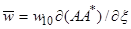
Система уравнений для функций 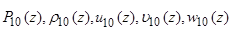 следует из (18) после подстановки (19) и (20) при использовании соотношений (16),(17). Данная система сводится к неоднородной системе линейных дифференциальных уравнений, которую запишем в матричном виде:
следует из (18) после подстановки (19) и (20) при использовании соотношений (16),(17). Данная система сводится к неоднородной системе линейных дифференциальных уравнений, которую запишем в матричном виде:

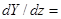
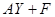 (21)
(21)
где А- матрица размрностью 8 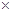 8, элементы которой являются постоянными (не зависящими от z величинами):
8, элементы которой являются постоянными (не зависящими от z величинами):
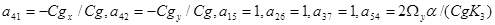
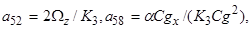
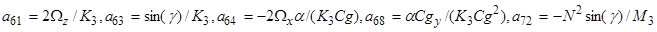
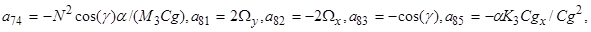
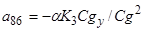
Все остальные элементы матрицы А равны 0. Столбцы 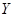 и
и 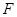 имеют вид:
имеют вид:
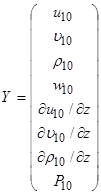
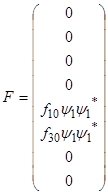
где 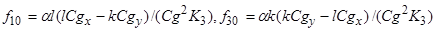
Система дифференциальных уравнений (21) решается аналитически при следующих граничных условиях: 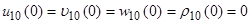 и
и 
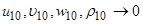 при
при 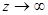 . Окончательно индуцируемые волной поля скорости течения
. Окончательно индуцируемые волной поля скорости течения 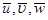 и плотности
и плотности 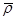 определяются по формулам:
определяются по формулам:
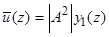 ,
, 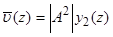 ,
, 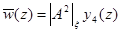 ,
, 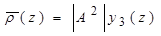
(22)
Амплитудный множитель 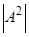 найдём из условия нормировки, которое состоит в следующем. Пусть
найдём из условия нормировки, которое состоит в следующем. Пусть 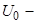 максимальная амплитуда волновой орбитальной скорости.
максимальная амплитуда волновой орбитальной скорости.
Тогда 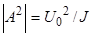 ,где
,где 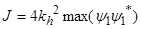 . (23)
. (23)
Пусть  (24) -осреднённое за период волны тангенциальное напряжение у дна. Следуя [15,16 ] введём коеффициент донного трения
(24) -осреднённое за период волны тангенциальное напряжение у дна. Следуя [15,16 ] введём коеффициент донного трения 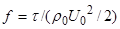 . При заданном
. При заданном 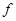 коэффициент вертикального турбулентного обмена для данной волны находится из (24).
коэффициент вертикального турбулентного обмена для данной волны находится из (24).
Если тангенциальное напряжение у дна превышает критическое значение 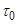 , соответствующее началу движения наносов, то волна взмучивает наносы, осуществляя их горизонтальный перенос. В стационарном и горизонтально -однородном случае уравнение вертикальной диффузии для средней концентрации наносов имеет вид [ 15 ]:
, соответствующее началу движения наносов, то волна взмучивает наносы, осуществляя их горизонтальный перенос. В стационарном и горизонтально -однородном случае уравнение вертикальной диффузии для средней концентрации наносов имеет вид [ 15 ]:
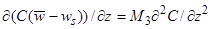 (25)
(25)
где 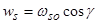 ,
, 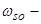 скорость гравитационного оседания наносов [15 ]. Решение уравнения (25), затухающее при удалении от дна имеет вид:
скорость гравитационного оседания наносов [15 ]. Решение уравнения (25), затухающее при удалении от дна имеет вид:
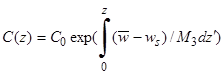 (26)
(26)
Здесь 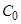 - концентрация наносов у дна, которая находится из следующего граничного условия. Пусть
- концентрация наносов у дна, которая находится из следующего граничного условия. Пусть 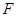 -вертикальный поток наносов у дна, тогда следуя работе [ 15]
-вертикальный поток наносов у дна, тогда следуя работе [ 15]
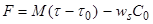 (27)
(27)
С другой стороны, вертикальный поток наносов равен 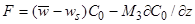 .
.
Учитывая, что у дна 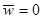 , найдём
, найдём 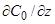 :
:
 (28)
(28)
Из (26) и (28) найдём 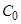 :
:
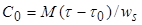 (29)
(29)
Учитывая, что при 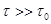
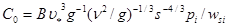 [16] величина
[16] величина 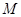 для i-ой фракции определяется по формуле:
для i-ой фракции определяется по формуле: 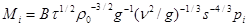 , где
, где 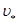 -динамическая скорость у дна,
-динамическая скорость у дна, 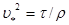
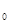
 ,
, 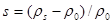 ,
,  -плотность материала наносов,
-плотность материала наносов, 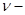 кинематическая вязкость жидкости,
кинематическая вязкость жидкости, 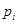 -содержание частиц i- ой фракции в материале дна. Для смеси фракций вертикальное распределение концентрации наносов имеет вид:
-содержание частиц i- ой фракции в материале дна. Для смеси фракций вертикальное распределение концентрации наносов имеет вид:
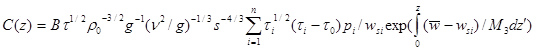 (30)
(30)
где 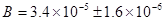
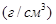 [16]
[16]
Найдём расход наносов вдоль и поперёк изобат:
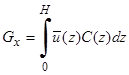
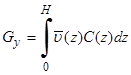 -
- 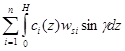 (31)
(31)
где 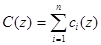 ,
, 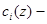 распределение концентрации
распределение концентрации 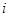 -ой фракции,
-ой фракции, 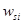 -скорость гравитационного осаждения i –ой фракции.
-скорость гравитационного осаждения i –ой фракции.
Расчёт индуцируемых полей скорости 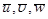 проводить будем проводить на континентальном склоне Южного берега Крыма между мысами Сарыч и Аю-Даг, где
проводить будем проводить на континентальном склоне Южного берега Крыма между мысами Сарыч и Аю-Даг, где 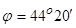 ,
, 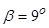 , средний уклон дна равен
, средний уклон дна равен 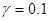 , при типичном значении частоты Брента-Вяйсяля глубже главного пикноклина ~ 3 цикл/час [1],
, при типичном значении частоты Брента-Вяйсяля глубже главного пикноклина ~ 3 цикл/час [1], 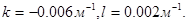 Коэффициент придонного трения
Коэффициент придонного трения 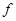 принимался равным
принимался равным 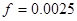 [15,17], соответствующим наиболее типичным условиям шероховатости морского дна на рассматриваемых масштабах.
[15,17], соответствующим наиболее типичным условиям шероховатости морского дна на рассматриваемых масштабах.
Нормирующий множитель А определялся таким образом, чтобы максимальная амплитуда горизонтальной скорости равнялась 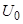 ~0.18 м/с, т.е. А находилось из соотношения (23). При
~0.18 м/с, т.е. А находилось из соотношения (23). При 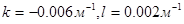 максимальное значение
максимальное значение 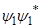 достигается при z=1.8 м. Коэффициент вертикального турбулентного обмена определялся из соотношения (24) при
достигается при z=1.8 м. Коэффициент вертикального турбулентного обмена определялся из соотношения (24) при 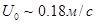 и составил
и составил 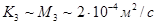 . Kоэффициент горизонтального турбулентного обмена выразим через
. Kоэффициент горизонтального турбулентного обмена выразим через  , следуя эмпирической зависимости коэффициента обмена от масштаба явления
, следуя эмпирической зависимости коэффициента обмена от масштаба явления 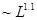 [18].
[18].
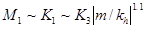
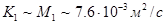 .Частота волны
.Частота волны 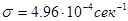 ,декремент затухания волны равен -
,декремент затухания волны равен - 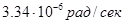 , При столь значительном уклоне дна необходим учёт в тангенциальном напряжении гравитационной составляющей, обусловленной наклоном дна в выражении для потока
, При столь значительном уклоне дна необходим учёт в тангенциальном напряжении гравитационной составляющей, обусловленной наклоном дна в выражении для потока  (27):
(27):
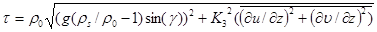 , (32)
, (32)
Для алевритовой фракции размером частиц 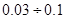
 мм величина
мм величина 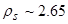
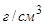 , критическое тангенциальное напряжение, соответствующее началу движения наносов
, критическое тангенциальное напряжение, соответствующее началу движения наносов 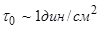 [19,20]. У фракций
[19,20]. У фракций 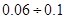 мм величина
мм величина 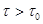 . Доля частиц указанных размеров составляет в донных осадках континентального склона
. Доля частиц указанных размеров составляет в донных осадках континентального склона 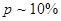 [21]. Доля фракций > 0.1 мм не превышает 1% [21,22]. Скорости гравитационного осаждения частиц фракций
[21]. Доля фракций > 0.1 мм не превышает 1% [21,22]. Скорости гравитационного осаждения частиц фракций  находились по формуле Стокса
находились по формуле Стокса  [23] и составили
[23] и составили 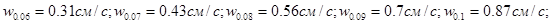
Донная концентрация взвешенных волной наносов равна  (или
(или 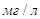 ) при равномерном распределении рассматриваемых частиц по размерам
) при равномерном распределении рассматриваемых частиц по размерам 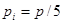 .
.
На рис. 1,2,3 показаны вертикальные профили индуцированного за счёт нелинейности компонент скорости среднего течения 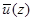 ,
,  ,
, 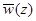 . Вертикальное распределение концентрации наносов, взвешенных волной показано на рис. 4. Расход наносов (44) вдоль и попрёк склона соответственно равен:
. Вертикальное распределение концентрации наносов, взвешенных волной показано на рис. 4. Расход наносов (44) вдоль и попрёк склона соответственно равен: 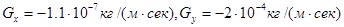 .
.
Выводы.
1. При распространении придонных топографических волн при наличии турбулентной вязкости и диффузии нелинейные эффекты проявляются в генерации средних на временном масштабе волны полей скорости течения и плотности.
2. При превышении турбулентного касательного напряжения у дна критического значения волна взмучивает донные осадки, осуществляя их горизонтальный перенос. Расмотренный механизм переноса наносов, по-видимому, является определяющим в поперечном переносе наносов на шельфе и континентальном склоне.
3. Концентрация взвешенной волной алевритовой фракции (~ 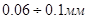 ) быстро убывает с удалением от дна, более мелкие фракции не взвешиваются волной. Расход наносов поперёк склона отрицателен и направлен вниз по склону, расход наносов вдоль изобат также отрицателен и сонаправлен с проекцией горизонтального волнового вектора.
) быстро убывает с удалением от дна, более мелкие фракции не взвешиваются волной. Расход наносов поперёк склона отрицателен и направлен вниз по склону, расход наносов вдоль изобат также отрицателен и сонаправлен с проекцией горизонтального волнового вектора.
Литература
1. Блатов А.С., Иванов В.А. Гидрология и гидродинамика шельфовой зоны Чёрного моря.- К.: "Наукова Думка", 1992.-237 с.
2. Михинов А.Е. Транспорт донных наносов в волновом потоке // Моделирование гидрофизических процессов в замкнутых водоёмах и морях.-М.:Наука,1989.-С.139-149.
3. Ястребов В.С., Парамонов А.Н. и др. Исследование придонного слоя буксируемыми аппоратами. М.: изд. ИО АН СССР, 1989, 128с.
4. Борисенко Ю. Д., Воронович А.Г., Леонов А.И., Миропольский Ю.З. К теории нестационарных слабонелинейных внутренних волн в стратифицированной жидкости // Изв. АН СССР ФАО.- 1976.-т. 12, N 3,- C. 293-301.
5. Grimshow R. The modulation of an internal gravity wave packet and the resonance with the mean motion.// Stud. In Appl. Math.- 1977.- v.56.-p.241-266.
6. Дворянинов Г.С. Эффекты волн в пограничных слоях атмосферы и океана.-Киев: Наукова Думка, 1982.-176 с.
7. Слепышев А.А. Процессы переноса, обусловленные слабонелинейными внутренними волнами при наличии турбулентности // Изв. РАН ФАО, 1997.- № 4, с. 536-548.
8. Ле Блон П., Майсек Л. Волны в океане. М.: Мир,1981,ч.1-478 с.
9. Brink K.H. A comparision of long coastal trapped waves theory with observation off Peru // J. Phys. Oceanogr.- 1982.-V.12.-No 8.-P. 897-913.
10. Rhines P. Edge-,bottom-,and Rossby waves in a rotating stratified fluid // Geophys. Fluid Dyn.-1970.-V.1-P.273-302.
11. Ou, H.-W. On the propogation of free topographic Rossby waves near continental margins. Part 1 Analitical model for a wedge // Journal of Physical Oceanography.--1980 -Vol. 10.-N 7.- P. 1051-1060.
12.Пантелеев Н.А. Слепышев А.А. Воздействие мелкомасштабной турбулентности на придонные топографические волны // Морской гидрофизический журнал.-2000, № 1-С. 3-18
13.Задорожный А.И. Затухание длинных волн в экспоненциально стратифицированном море // Морские гидрофизические исследования.-1975,№3.-С 96-110.
14. Черкесов Л.В. Гидродинамика волн, Киев: Наукова Думка.-1980.-259 с.
15. Шапиро Г.И., Аквис Т.М., Пыхов Н.В., Анциферов С.М. Перенос мелкодисперсного осадочного материала мезомасштабными течениями в шельфово-склоновой зоне моря // Океанология.-2000.-Том 40.-№ 3.-С. 333-339.
16. Анциферов С.М., Дебольский В.К Распределение концентрации взвесей в стационарном потоке над размываемым дном.// Водные ресурсы.- 1997.-Том 24.- № 3.-с.270-276.
17. Green O., McCave I.N. Seabed drag coefficient under tidal currents in the eastern Irish Sea// Journal of Geophysical Research- 1995.-Vol. 100.- № C8.-P. 16057-16069.
18. Озмидов Р.В. Диффузия примесей в океане.-Л.: Гидрометеоиздат.-1986.-280 с.
19. Uncles R.J., Stephens J.A. Distribution of suspended sediment at high water in a macrotidal estuary // J.Geophys. Res.-1989.-V.94.-P.14395-14405.
20. Van Rijn L. Principles of sediment transport in rivers, estuaries and coastal seas. Aqual Publ.-1993.-720 p.
21. Щербаков Ф.А, Куприн П.Н., Потапова Л.И., Поляков А.С., Забелина Э.К., Сорокин В.М. Осадконакопление на континентальной окраине Чёрного моря.-М.: Наука,1978.-210с.
22. Айтбулатов Н.А. Динамика твёрдого вещества в шельфовой зоне.Л.: Гидрометеоиздат, 1990.-271с.
23. Шамов Г.И. Речные наносы.-Л.: Гидрометеоиздат,1959.-378с.
УДК 551.466.8
А Н Н О Т А Ц И Я
К статье Слепышева А.А. "Транспортные свойства придонных топографических волн на шельфе и континентальном склоне."
В приближении Буссинеска для захваченных наклонным дном топографических волн определены средние течения, индуцированные волной за счёт нелинейности
при наличии стока энергии волны в турбулентность для плоского склона произвольной ориентации. В диффузионном приближении находится вертикальное распределение концентрации наносов, взвешенных волной. Определяется расход наносов вдоль и поперёк изобат.
Ответ
рецензенту статьи Слепышева А.А. «Транспортные свойства придонных топографических волн на шельфе и континентальном склоне»
Автор доработал статью в соответствии с замечаниями рецензента. Первая часть статьи сокращена, в частности, Приложение, на которое есть ссылка в первой части статьи, убрано, т. к. предложенный метод аналитического решения системы дифференциалных уравнений общеизвестен.
5.03.2002 г. А.А. Слепышев
Редакции журнала
«Физика атмосферы и океана»
Пыжевский пер., д.3
Москва, Ж-17, 109017
Россия
Глубокоуважаемая редакция!
Высылаю два доработанных и один первоначальный варианты статьи
Слепышева А.А. «Транспортные свойства придонных топографических волн на шельфе и континентальном склоне». Статья доработана в соответствии с замечанием рецензента, в частности, сокращена первая часть статьи и Прил
 2020-01-14
2020-01-14 103
103






