Сущность и структура решения задач

Что значит решить задачу? Можно ответить так: решить задачу – это значит найти ее ответ. В какой-то степени это верно, но все дело в том, как понимать слово «найти». Можно ли считать, что человек решил задачу, если он, например, подсмотрел в ответы задачника, ведь он по сути нашел ответ. Очевидно, что нет. Значит, решение задачи состоит не просто в том, чтобы найти ответ. Чтобы разобраться в этом, придется внимательно приглядеться к процессу решения задачи.

Задача4. Длины оснований трапеции равны 4см и 10см. Найти длины отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

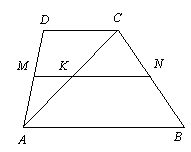Сначала посмотрим схематическую запись задачи.

Дано:

см; см.

Найти: 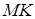 и .

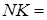Решение. Как известно, средняя линия трапеции параллельна ее основаниям. Значит,  и . Диагональ  делит трапецию на два треугольника. Рассмотрим каждый из них. В треугольник  отрезок  является средней линией, ибо  как часть отрезка , и точка  по условию есть середина стороны . А средняя линия треугольника равна половине основания. Значит, , а так как см, то 5см.

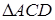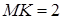Аналогично, рассматривая , мы убеждаемся, что  есть средняя линия этого треугольника и поэтому , но см, следовательно, см.

Итак, искомые длины отрезков найдены, задача решена.

Приведенное решение можно представить в виде схемы.

№ шага	Общие положения математики	Условия задачи или их следствия	Результат
1	Средняя линия трапеции параллельна ее основаниям.	MN – средняя линия трапеции ABCD.	MN//AB, MN//CD/
2	Диагональ делит трапецию на два треугольника.	ABCD – трапеция, AC – ее диагональ.	ABC и ACD – треугольники.
3-4	Отрезок, проходящий через середину стороны треугольника параллельно другой стороне, является средней линией треугольника.	В ΔABC точка N – середина BC и NK//AB, в ΔACD точка M - середина AD и MK//CD.	NK – средняя линия ΔABC, MK – средняя линия ΔACD.
5-6	Средняя линия треугольника равна половине основания.	NK – средняя линия ΔABC, AB=10см, MK – средняя линия ΔACD, CD=4см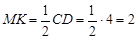.	см см

 

Из приведенных примеров можно сделать следующий вывод:

Решить задачу – это значит найти такую последовательность общих положений математики (определений, аксиом, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения), получаем то, что требуется в задаче, - ее ответ.

На приведенное определение следует смотреть как на первичное, самое общее толкование сущности решения задач.

Если под процессом решения задач понимать процесс, начинается с момента получения задачи до момента полного завершения ее решения, то, очевидно, что этот процесс состоит не только из изложения уже найденного решения, а из ряда этапов, одним из которых и является изложение решения.

Итак, весь процесс решения задачи можно разделить на восемь этапов:

1. анализ задачи;

2. схематическая запись задачи;

3. поиск способа решения задачи;

4. осуществление решения задачи;

5. проверка решения задачи;

6. исследование решения;

7. формулирование ответа задачи;

8. познавательный анализ решения задачи.

 

Поиск плана решения задачи

Поиск плана решения составляет центральную часть всего процесса решения. Найдя план, его осуществление уже не составляет особого труда, оно требует лишь технических умений выполнения тех действий и операций, которые изучаются в курсе математики.

Однако начинать процесс решения задачи надо с глубокого и всестороннего анализа задачи и построения ее схематической записи, целью проведения которой является поиск плана решения задачи.

Сформулируем основные рекомендации для поиска решения математических задач.

1. Прочтя задачу, надо попытаться установить, к какому виду задач она принадлежит (стандартная, нестандартная).

2. Если вы узнали в ней стандартную задачу знакомого вида, то примените для ее решения известное вам общее правило.

3. Если же задача не является стандартной, то следует действовать в следующих направлениях:

а) вычленять из задачи или разбивать ее на подзадачи стандартного вида (способ разбиения);

б) ввести в условие вспомогательные элементы: вспомогательные параметры, вспомогательные построения (способ вспомогательных элементов);

в) переформулировать ее, заменить ее другой равносильной задачей (способ моделирования).

4.    Для того, чтобы легче было осуществлять указанные способы, полезно предварительно построить наглядную вспомогательную модель задачи – ее схематическую запись.

5.    Решение нестандартных задач есть искусство, которым можно овладеть лишь в результате глубокого постоянного самоанализа действий по решению задач и постоянной тренировки в решении разнообразных задач.

 

Классификация планиметрических задач с использованием тригонометрии.

В основном применение тригонометрии при решении геометрических задач идет по четырем направлениям:

1) использование формулы площади треугольника;

2) использование соотношений между сторонами и углами в прямоугольном треугольнике:

       а) по определению синуса, косинуса, тангенса и котангенса углов;

       б) применение тождественных преобразований;

3) использование двух «теорем-тружеников» - теоремы синусов и теоремы косинусов;

4) при решении практических задач.

5.1. Решение задач методом площадей.

Задача1. Площадь равнобочной трапеции равна 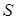, угол между ее диагоналями, противолежащей боковой стороне, равен . Найти высоту трапеции.

Решение.

1-2. Анализ и схематическая запись задачи. Расчленим условие задачи на несколько составляющих. Условие «площадь равнобочной трапеции равна 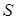» говорит нам о следующем: 1) дана трапеция; б) данная трапеция равнобочная, то есть ее боковые стороны равны (а также ее диагонали); в) и площадь этой трапеции равна .

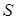Из следующего фрагмента условия «угол между ее диагоналями, противолежащей боковой стороне, равен » выделим следующие положения: г) в данной трапеции проведены диагонали; д) угол, образованный этими диагоналями, и лежащий напротив боковой стороны трапеции, равен .

И собственно вопрос задачи: найти высоту трапеции.

На основе полученных данных мы можем сделать краткую запись и построить схематический рисунок:

Дано:  - трапеция, , , , .

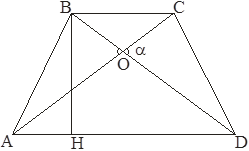Найти: .

 

3-5. Поиск и осуществление решения. Исследование задачи. Эти три этапа процесса решения в данном случае удобно производить совместно. Мы знаем формулу нахождения площади трапеции по диагоналям и углу между ними:

,

отсюда найдем длину диагонали:

.

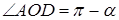Рассмотрим . Этот треугольник прямоугольный; нам известна длина диагонали и если мы можем найти один угол, то найдем и сторону . Найдем угол . , тогда . Так как точка пересечения диагоналей делит их пополам, то полученный треугольник  будет равнобедренным. Так как 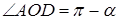, то сумма углов  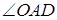и  равна , а так как углы при основании в равнобедренном треугольнике равны, то каждый из них равен . Тогда по определению синуса угла найдем сторону : 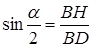, отсюда

.

6.    Проверка решения. В данном случае проверка решения сводится к тому, чтобы убедиться, что по найденной формуле действительно можно вычислить  такое, которое принадлежит области его определения. Очевидно, что должно соблюдаться лишь одно условие: . Так как по условию задачи  может изменяться от  до , то  будет всегда положительным; переменная  всегда положительна, значит, условие 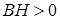 выполняется в любом случае.

7.    Ответ. .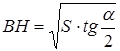

8.    Исследование решения. При решении задачи надо анализировать каждый шаг решения с точки зрения его выполнимости при предварительно найденных или заданных условиях и при необходимости эти условия уточнять, суживая тем самым области изменения параметров.

Задача2. В равнобедренном треугольнике  угол  равен . Окружность радиусом 1 касается боковых сторон  и  треугольника и пересекает его основание  в точках  и  (точка  лежит между  и );  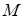- точка касания окружности и стороны ; 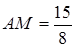. Вычислить площадь .

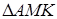Дано:  - равнобедренный, ,  - окружность радиуса 1, .

Найти: .

Решение: Прежде всего, нужно провести расчеты, которые позволят выяснить местоположение центра окружности; пока лишь ясно, что этот центр лежит на высоте  равнобедренного , так как стороны  и  - касательные к окружности, а потому центр окружности лежит на биссектрисе  угла между этими касательными.

Введем обозначение: . Проведем радиус  в точку касания , тогда  тоже равен  (  и  - углы со взаимно-перпендикулярными сторонами). По условию . Воспользовавшись формулой , получим ; тогда .

Из  находим: ; 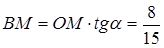. Далее,

; .

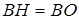Это значит, что , а потому точки  и  должны совпадать, т.е. для дальнейшего решения задачи надо сделать новый (правильный) рисунок.

Площадь треугольника  будем искать по формуле . Известно, что .

Таким образом, задача свелась к отысканию длины отрезка .

Воспользуемся тем, что . Положим , тогда , и получим уравнение , откуда 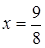. Тогда  и, следовательно,

.

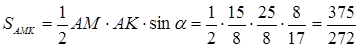Ответ: .

 

Задача3. Найти площадь  с углами , зная, что расстояние от произвольной точки 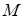, взятой внутри треугольника, до его сторон равны соответственно ,  и .

Дано: , .

Найти: .

Решение: Площадь  можно найти по формуле 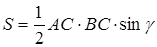, но для этого надо найти  и . Положим . Тогда по теореме синусов

,

откуда находим: .

Итак, задача сводится к отысканию значения .

Для составления уравнения применим метод площадей: выберем в качестве опорного элемента площадь 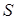 треугольника .

С одной стороны,

.

С другой стороны,

.

Значит, , откуда находим:

.

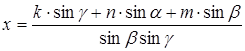Подставив это значение  в первую из отмеченных выше формул для площади , получим:

.

Ответ: .

 

Замечание. Какие же средства используются для составления уравнений в геометрических задачах или, иными словами, какие геометрические факты используются для составления уравнений? Перечислим эти факты:

- теорема Пифагора;

- теорема о биссектрисе треугольника;

- пропорциональность сторон или других линейных элементов в подобных треугольниках;

- метрические соотношения в прямоугольном треугольнике (включая тригонометрические соотношения между сторонами и углами), параллелограмме, окружности;

- различные формулы для вычисления площадей (прежде всего, треугольников);

- теорема синусов, теорема косинусов.

5.2. Решение задач на применение определения синуса, косинуса.

Задача4. Найдите площадь равнобедренной трапеции, зная длину ее диагонали  и величину угла  между этой диагональю и большим основанием.

Решение.

1. Анализ условия задачи. Читая условие задачи, выделяем нужные моменты: а) дана трапеция; б) ее боковые стороны равны; в) длина диагонали ее равна 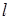; г) угол между диагональю и большим основанием равно .

Выясняем вопрос задачи: необходимо найти площадь трапеции.

2. Схематическая запись задачи. Сделаем рисунок и запишем краткую запись.

Дано:  - трапеция, , , .

Найти: .

 

3-5. Поиск и осуществление решения. Исследование задачи. Запишем формулу для нахождения площади трапеции.

,

где  - высота трапеции.

Из треугольника  по определению синуса найдем высоту трапеции:

,

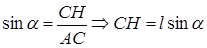тогда по теореме Пифагора имеем:

.

Так как  равна средней линии трапеции, то

.

Теперь найдем площадь трапеции:

.

6.    Проверка решения. Очевидно, что данное решение верно для любых значений .

7.    Ответ. .

8.    Исследование решения. Каким бы ни были параметры  и 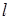, задача всегда имеет единственное решение.

Задача5. В равнобедренной трапеции диагональ перпендикулярна к боковой стороне и равна , острый угол трапеции . Найти площадь трапеции.

Дано:  - равнобедренная трапеция, , , .

Найти: .

Решение: Площадь трапеции:

,

где три неизвестных. Найдем их.

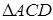Из : ; из : .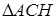

Рассмотрим .

;

Тогда,

.

Теперь мы можем найти площадь:

.

Ответ: .

Задача6. В параллелограмме высоты равны  и , угол между ними . Найти его площадь.

Дано:  - параллелограмм, , - высоты параллелограмма,  - точка пересечения высот, .

Найти: .

Решение: Треугольник  - прямоугольный, тогда . Из треугольника  найдем:

.

Тогда по формуле площади параллелограмма:

.

Ответ:

Замечание. Зная стороны прямоугольного треугольника, мы можем найти его острые углы. Сначала находим один из синусов этих углов, используя равенства , . Затем по найденному синусу находим величину этого угла. Второй угол дополняет найденный до .

Или решается обратная задача: по острому углу и одной из сторон прямоугольного треугольника найти остальные его элементы. Возможны два случая: 1) даны острый угол и гипотенуза; 2) даны острый угол и катет.

5.3. Решение задач на применение определения тангенса, котангенса.

Задача7. В прямоугольном треугольнике найти угол между медианой и биссектрисой, проведенными из вершины острого угла, равного .

1-2. Анализ и схематическая запись задачи. Эта задача содержит такие условия: а) дан прямоугольный треугольник; б) из вершины острого угла проведена медиана; в) из вершины этого же угла проведена биссектриса; в) величина данного угла равна . И вопрос задачи: найти угол между медианой и биссектрисой. На основе этого сделаем краткую запись и нарисуем чертеж.

Дано:  - прямоугольный,  - биссектриса, 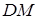 - медиана, , , .

Найти: .

3-5. Поиск и осуществление решения. Исследование задачи. Обозначим искомый угол через . Тогда из  найдем

,

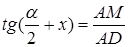с другой стороны из  

,

отсюда выразим

.

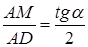Подставляя последнее равенство в первое, найдем:

; ; .

6. Проверка решения. По условию задачи на переменные нет ограничений, значит найденная формула выполняется в любом случае.

7. Ответ. .

8. Исследование решения.

 

Задача8. Высота равнобочной трапеции равна , а угол между диагоналями, противолежащий боковой стороне, равен 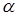. Найти среднюю линию трапеции.

Дано:  - равнобочная трапеция, ,  - диагонали, .

Найти: среднюю линию.

Решение: Рассмотрим , как смежный к . Тогда , и

 

.

А  есть величина, равная средней линии трапеции.

Ответ: .

Задача9. В равнобедренной трапеции острый угол равен , радиус вписанного круга . Найти площадь трапеции.

Дано:  - равнобочная трапеция,  - окружность с центром в точке  и радиусом , .

Найти: .

Решение: Запишем формулу площади трапеции:

,

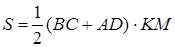следовательно, мы имеем две неизвестные ().

Рассмотрим . Применяя определение тангенса, найдем основание :

.

Из 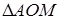 найдем ():

.

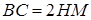Тогда ; и , , следовательно, имеем:

.

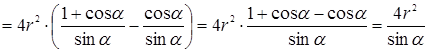Ответ: .

 

Задача10. В равнобедренном треугольнике величина угла при вершине равна 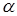, а площадь его равна . Найти длину основания треугольника.

Дано:  - равнобедренный, , , .

Найти: .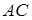

Решение: Запишем формулу нахождения площади треугольника: . Здесь два неизвестных: длины основания и высоты. Через тангенс угла найдем высоту.

.

Подставим полученное значение в формулу площади и выразим основание треугольника:

,

,

.

Ответ: .

5.4. Решение задач на применение теорем синуса, косинуса.

Задача11. Длина основания равнобедренного треугольника равна , а угол при вершине - . Найти длину биссектрисы, проведенной к боковой стороне.

Решение.

1-2. Анализ и схематическая запись задачи. Расчленим условие задачи на составляющие: 1) дан треугольник; б) данный треугольник равнобедренный, то есть его боковые стороны равны; в) длина основания треугольника ; г) угол, лежащий напротив основания, равен ; д) из угла при основании (так как треугольник равнобедренный, не имеет значения из которого угла) проведена биссектриса.

И вопрос задачи: найти длину биссектрисы.

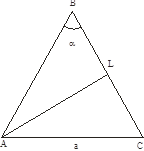На основе полученных данных мы можем сделать краткую запись и построить схематический рисунок:

Дано:  - треугольник, , ,  - биссектриса, , .

Найти: .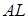

 

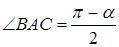3-5. Поиск и осуществление решения. Исследование задачи. Так как треугольник равнобедренный, то углы при основании равны, следовательно , тогда . Так как  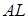- биссектриса, то . Тогда из треугольника  по теореме синусов:

.

Так как  и , то

.

Отсюда найдем биссектрису :

.

 

6.    Проверка решения. Очевидно, что данное решение верно для любых значений .

7.    Ответ. .

8.    Исследование решения. Каким бы ни были параметры  и , задача всегда имеет единственное решение.

 

Задача12. Один из углов трапеции равен , а боковые стороны при продолжении пересекаются под прямым углом. Найдите меньшую боковую сторону трапеции, если ее средняя линия равна 10 см, а одно из оснований – 8 см.

Дано: 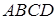 - трапеция,  - средняя линия, , , , .

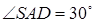Найти: .

Решение: По определению средней линии 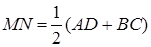, отсюда найдем большее основание трапеции:

.

Рассмотрим треугольник 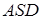. По теореме синусов найдем сторону :

.

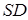Так как треугольники  и  подобны, то . Из треугольника :

;

.

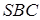Ответ: 2.

 

Задача13. В треугольнике  известно, что  и . На стороне  взята точка  так, что . Найти отношение радиуса окружности, описанной около , к радиусу окружности, вписанной в .

Дано: , , , .

Найти: .

Решение. Введем вспомогательный параметр . Тогда .

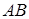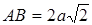Чтобы найти радиус  окружности, описанной около треугольника , вычислим сторону  по теореме косинусов, а затем воспользуемся теоремой синусов. Имеем: , т.е. , откуда находим, что . По условию , значит, . По теореме синусов , значит, , откуда находим .

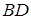Радиус  окружности, вписанной в треугольник , найдем по формуле , где  - площадь,  - полупериметр . Уже известно, что . Сторону  найдем из  по теореме косинусов: 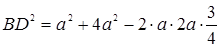, откуда . Значит, . Площадь  треугольника  вычислим по формуле Герона:

.

Значит,

.

Ответ: .

 

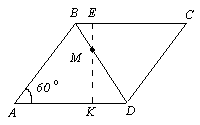
Задача14. В ромбе  со стороной  и острым углом  проведен отрезок  (), который пересекает диагональ  в точке 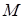 так, что 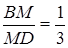. Известно, что . Найти длину отрезка .

Дано: 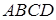 - ромб, , , , , , .

Найти: .

Решение: Положим 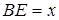; тогда из подобия треугольников  и  следует, что 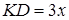 (поскольку ). Тогда . Введем еще одно обозначение:  - высота ромба  и одновременно – высота трапеции  и высота трапеции .

;

.

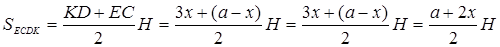По условию , значит, , откуда .

Нам нужно найти длину отрезка . Сначала найдем длину , для чего воспользуемся «выносным» чертежом. Рассмотрим трапецию , в которой 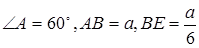 (напомним, что , а ),  (напомним, что , т.е. ).

Проведем отрезок 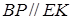, тогда

.

Применим к  теорему косинусов:

;

.

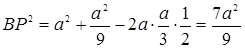Значит, .

Так как , то .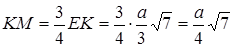

Ответ: .

 

Задача15. Дан остроугольный треугольник , в котором ; ; 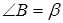. В каком отношении ортоцентр делит высоту, проведенную из вершины ?

Дано: , , , ,  - высота.

Найти: .

Решение: Опишем около  окружность, радиус которой обозначим через  (вспомогательный параметр).

Проведем  и учтем, что , где  - ортоцентр.

Рассмотрим . Так как  измеряется дугой , , а 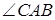 измеряется половиной дуги 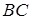, то . Тогда .

По теореме синусов, примененной к , , значит, , и тогда из  получаем: .

;

.

Итак, .

Ответ: .

Замечание. Задача «решить треугольник по некоторым заданным его элементам» может рассматриваться в двух вариантах.

а) Имеется треугольник, и известны некоторые его элементы. Найти остальные его элементы.

б) Заданы некоторые отрезки и углы (или их величины). Найти (построить) треугольник, для которого заданные отрезки и углы являются заданными его элементами.

Теорема синусов позволяет решить треугольник по стороне и двум углам и по двум сторонам и углу против одной из них.

5.5. Решение задач на применение тождественных преобразований.

Задача16. Около круга радиуса  описан равнобедренный треугольник с углом . Определите стороны треугольника.

Решение.

1. Анализ условия задачи. Выделим основные данные из условия задачи: а) дан круг радиуса  (пусть его центр находится в точке

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: