*******
Примечание
1. Понятно, что приведенное доказательство «Утверждения 2» для q = 4 = 2m, где m = 2, распространяется и на показатель степени q=2m при m>2 – натуральном.
2. Если уравнение al+ b4 = c4, где  ≥2 - четное, неразрешимо в попарно простых целых числах a, b, и c, то и уравнение a4+ b4 = c4 не только неразрешимо в этих же числах, но и вообще неразрешимо ни в каких других целых числах ( не являющихся попарно взаимно простыми целыми числами).
≥2 - четное, неразрешимо в попарно простых целых числах a, b, и c, то и уравнение a4+ b4 = c4 не только неразрешимо в этих же числах, но и вообще неразрешимо ни в каких других целых числах ( не являющихся попарно взаимно простыми целыми числами).
Вывод:Великая теорема Ферма для показателя l= q = 4 доказана.
3. Результат доказательства, а именно четность чисел a, b, c в уравнении al+ b4 = c4 (  ≥2 - четное), а, следовательно, в уравнении a4+ b4 = c4 дает возможность в этом уравнении применить метод бесконечного спуска, о чем в свое время не только упоминалось самим Ферма, но и им использовалось.
≥2 - четное), а, следовательно, в уравнении a4+ b4 = c4 дает возможность в этом уравнении применить метод бесконечного спуска, о чем в свое время не только упоминалось самим Ферма, но и им использовалось.
На основании Выводов о Великой теореме Ферма (стр.34, стр.49) получаем окончательный вывод.
Окончательный «Вывод»: Великая теорема Ферма доказана.
********
Утверждение 3
Часть 1
Уравнение  (
( ≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах
≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах  ,
,  и
и  таких, чтобы
таких, чтобы  - было четным,
- было четным,  и
и  - нечетными целыми числами.
- нечетными целыми числами.
Часть 2
Возможны случаи: либо b = ± 1, либо c = ± 1.
*********
Часть первая (Утверждения 3)
Уравнение  (
( ≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах
≥ 3 – нечетное натуральное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах  ,
,  и
и  таких, чтобы
таких, чтобы  - было четным,
- было четным,  и
и  - нечетными целыми числами.
- нечетными целыми числами.
Доказательство
Первая часть доказательства «Утверждения 3» аналогична «Части первой» доказательства «Утверждения 2».
Итак, имеем уравнение  (1), где
(1), где  ≥ 3 – нечетное натуральное, числа a, b, c (если, конечно, они существуют) – попарно взаимно простые целые числа (это наше допущение – вопреки «Утверждению 3»), среди которых только одно четное число a.
≥ 3 – нечетное натуральное, числа a, b, c (если, конечно, они существуют) – попарно взаимно простые целые числа (это наше допущение – вопреки «Утверждению 3»), среди которых только одно четное число a.
Из уравнения (1) следует:
 =>
=>  (2).
(2).
Пусть  (3), где
(3), где  и β - целые числа, отличные от нуля и c2 + b2 = 2 β (4), где β – нечетное число при с и b – нечетных.
и β - целые числа, отличные от нуля и c2 + b2 = 2 β (4), где β – нечетное число при с и b – нечетных.
******
Примечание
То, что β в уравнении (4) нечетное число, хорошо известный факт в теории чисел, который мы ранее уже учитывали («Примечание», стр. 35).
Представим нечетные числа b и c в виде:
b = 2n1 + 1; c = 2n2 + 1, где n1 и n2 - произвольные целые числа. Тогда
b2 + c2 = (2n1 + 1)2 + (2n2 + 1)2 = 2 [2 (n12+n22+n1+n2) + 1],
где в квадратных скобках нечетное число, что и требовалось доказать
*******
Тогда из уравнения (2) следует (с учетом (3) и (4)):
 =
= 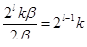 , где c2 + b2 ≠ 0, т.к. c ≠ 0, b ≠ 0, т.е.
, где c2 + b2 ≠ 0, т.к. c ≠ 0, b ≠ 0, т.е.
 (5),
(5),
где k – целое число, отличное от нуля, т.к. c и b взаимно простые целые числа.
Из соотношений (4) и (5 ) определяем b2 и c2:
 =>
=>  =>
=> 
Откуда β = b2 + 2l-2k (8) - нечетное число (из (4)) при b – нечетном и 2l-2k - четном, т.к.  ≥ 3 – нечетное натуральное число.
≥ 3 – нечетное натуральное число.
Вывод:
1. Из соотношения (4) имеем:
(9) 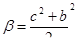 - нечетное число.
- нечетное число.
2. Из соотношения (5) имеем:
(10)  пропорционально 2 (явно), т.е.
пропорционально 2 (явно), т.е. 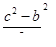 - четное число.
- четное число.
Это дополнительная информация о свойствах предполагаемых взаимно простых числах  , которая в дальнейшем нам очень пригодится.
, которая в дальнейшем нам очень пригодится.
*******
Теперь попробуем выразить сумму четвертых степеней чисел c и 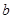 . Учитывая соотношения (6) и (7), получим:
. Учитывая соотношения (6) и (7), получим:


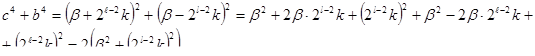 ,
,
т.е. 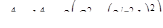 (11),
(11),
где  - целые числа, которые, в свою очередь, как мы знаем из предыдущего доказательства «Утверждения 1» (для
- целые числа, которые, в свою очередь, как мы знаем из предыдущего доказательства «Утверждения 1» (для  ), могут быть выражены через другие целые числа
), могут быть выражены через другие целые числа  следующим образом:
следующим образом:
(12) 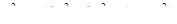 - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(13)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(14)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(15)  - четное число.
- четное число.
Примечание: во всех последующих исследованиях (Случаях) нас не будут интересовать t =0 и r=0 (при t =0  и
и  - четные из (12) и (13), при r=0
- четные из (12) и (13), при r=0  = 0 (из (15)) => а = 0 (из (3)), что противоречит нашему допущению).
= 0 (из (15)) => а = 0 (из (3)), что противоречит нашему допущению).
Для простоты опять ( как в утверждениях 1 и 2 ) обозначим правые части уравнений (12), …, (15) буквами С, В, N, К, т.е.
 = С
= С
 = В
= В
 = N
= N
 = К,
= К,
и рассмотрим с лучай, когда в правых частях уравнений (12), …, (15) перед С, В, N, К, стоят «плюсы» и выполняется Условие1.
Условие1 (начало).
с 2 = С
b2 = B
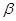 = N
= N

Случай «+».
(12+)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(13+)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(14+)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(15+)  - четное число.
- четное число.
Казалось бы, все нормально: четность чисел  в (12+), …, (15+) совпадают при
в (12+), …, (15+) совпадают при  -нечетном с нашими предыдущими рассуждениями.
-нечетном с нашими предыдущими рассуждениями.
Однако не все так просто.
Помимо всего прочего, у нас есть еще две дополнительные информации (9) и (10) (о четности, заключенной в «Выводе» (стр.36)), вытекающие из предположения о том, что, вопреки условию «Утверждения 2», допустим, существуют попарно взаимно простые целые числа  .
.
Попробуем найти сумму  , воспользовавшись их выражениями (12+) и (13+):
, воспользовавшись их выражениями (12+) и (13+):
 ,
,
т.е.  => (
=> ( ) пропорционально 4, откуда следует, учитывая (9) в «Выводе» (стр.36),
) пропорционально 4, откуда следует, учитывая (9) в «Выводе» (стр.36),
 !
!
Т.е ., вопреки «Выводу», 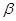 является не нечетным, а четным числом, что возможно (из (14)) при
является не нечетным, а четным числом, что возможно (из (14)) при  - четном.
- четном.
Однако, если  - четное, то
- четное, то  (в (12+) и (13+)) являются четными, т.е. в уравнениях (2)
(в (12+) и (13+)) являются четными, т.е. в уравнениях (2)  и (1)
и (1)  числа
числа  - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию в Случае «+» с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых 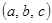 решений.
решений.
*******
Вывод. Следовательно, это уравнение (1)  в данном Условии 1(начало) не имеет решений в целых попарно взаимно простых
в данном Условии 1(начало) не имеет решений в целых попарно взаимно простых 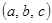 отличных от нуля числах, где
отличных от нуля числах, где  - нечетное натуральное число.
- нечетное натуральное число.
********
Мы рассмотрели случай, когда перед скобками в (12+), …, (15+) стояли «плюсы».
Случай, когда перед теми же скобками стоят «минусы» (Случай «-»), аналогичен вышерассмотренному. Вывод тот же. (Смотри Случай «-» на стр.8.)
*********
Примечание
Осталось рассмотреть еще 14 случаев, когда перед С, В, N, К стоятвсевозможные знаки (плюсы и минусы). Но об этом - во 2-ой части данного Утверждения 3.
********
Т.к. уравнение (11) симметрично для с 2 и b 2, (для уравнения 11 они равнозначны), то с 2 и b 2могут меняться своими выражениями (C и В). Это свойство назовем «новым свойством  ». Поэтому аналогичны вышерассмотренному и случаи («Новые» случаи «+» и «-»), когда опять же перед теми же скобками стоят одинаковые знаки.
». Поэтому аналогичны вышерассмотренному и случаи («Новые» случаи «+» и «-»), когда опять же перед теми же скобками стоят одинаковые знаки.
Условие 2 (начало).
с 2 = В
b2 = С
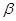 = N
= N

«Новые» случаи «+» и «-».
(12´±) c2 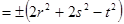 =± В
=± В
(13´±) b 2  =± С
=± С
(14±)  =± N
=± N
(15±) 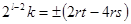 =± К.
=± К.
И в этом случае сумма  пропорциональна 4, откуда следует, (учитывая (13) в «Выводе» (стр.36)),
пропорциональна 4, откуда следует, (учитывая (13) в «Выводе» (стр.36)),  !
!
Т.е., вопреки «Выводу», и в этих «Новых» случаях «+» и «-» 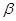 является не нечетным, а четным числом, что возможно(из (14±)) при
является не нечетным, а четным числом, что возможно(из (14±)) при  - четном.
- четном.
Однако, если  - четное, то
- четное, то  (в ( (12´±) и ( (13´±) ) являются четными, т.е. в уравнениях (2) и (1) числа
(в ( (12´±) и ( (13´±) ) являются четными, т.е. в уравнениях (2) и (1) числа  - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию ( в «Новых» случаях «+» и «-») с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых 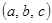 решений.
решений.
********
Вывод. Следовательно, это уравнение (1) в данном Условии 2 (начало) не имеет решений в целых попарно взаимно простых 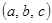 отличных от нуля числах.
отличных от нуля числах.
*******
Примечание
Осталось исследовать еще 14 случаев,рассматривающих «новые свойства  », когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
», когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
Но об этом во 2-ой части данного Утверждения 3.
********
Уравнение (11) симметрично и для 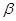 и для
и для 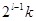 (для уравнения (11) они равнозначны), которые тоже могут меняться своими выражениями (N и К). Это свойство назовем «похожим свойством
(для уравнения (11) они равнозначны), которые тоже могут меняться своими выражениями (N и К). Это свойство назовем «похожим свойством 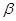 и
и 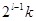 ». А это означает, что нам придется рассмотреть еще 16 «похожих» случаев (с 1-го по 14 и случаи «+» и «-», в которых
». А это означает, что нам придется рассмотреть еще 16 «похожих» случаев (с 1-го по 14 и случаи «+» и «-», в которых 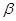 и
и 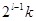 меняются своими выражениями (N и К)).
меняются своими выражениями (N и К)).
Условие 3.
с 2 = С
b2 = B
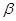 = К
= К

«Похожие» случаи «+» и «-».
(12±) c2 = ± ( ) = ± С
) = ± С
(13±) b 2 = ± ( ) = ± В
) = ± В
(14´±) 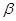 =
=  = ± К
= ± К
(15´±) 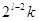
 = ± N.
= ± N.
Согласно одному из Выводов (формула (10)  пропорционально 2 (явно), при
пропорционально 2 (явно), при  . Но это возможно, глядя на четное (15´±)
. Но это возможно, глядя на четное (15´±)  = ±N= ±(
= ±N= ±( ) только при t-четном, при которых в (12±) и (13±) c и b – четные, чего не должно быть.
) только при t-четном, при которых в (12±) и (13±) c и b – четные, чего не должно быть.
Мы пришли к противоречию ( в «Похожих» случаях «+» и «-») с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых 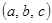 решений.
решений.
*******
В остальных 14 «похожих» случаях, где опять же  = ± N= ± (
= ± N= ± (  ) и перед С, В, N, К стоятвсевозможные знаки (плюсы и минусы), рассуждая аналогичным способом (и при этом не затрагивая «новые свойства
) и перед С, В, N, К стоятвсевозможные знаки (плюсы и минусы), рассуждая аналогичным способом (и при этом не затрагивая «новые свойства  » ( пояснение (стр.10), подобное для
» ( пояснение (стр.10), подобное для  проведено при доказательстве Утверждения 1 ), мы придем к прежнему результату: c и b – четные, чего не должно быть.
проведено при доказательстве Утверждения 1 ), мы придем к прежнему результату: c и b – четные, чего не должно быть.
Это значит, что мы опять придем к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых 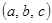 решений.
решений.
********
Вывод. Следовательно, это уравнение (1) в данном Условии 3 не имеет решений в целых попарно взаимно простых 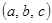 отличных от нуля числах.
отличных от нуля числах.
*******
Вывод
1. Таким образом, в вышерассмотренных Условиях 1 (начало), 2 (начало) и 3 уравнение (1)  (1), где
(1), где  ≥ 3 – нечетное натуральное число, не имеет решений в целых попарно взаимно простых
≥ 3 – нечетное натуральное число, не имеет решений в целых попарно взаимно простых 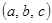 отличных от нуля числах.
отличных от нуля числах.
2. 1-я часть «Утверждения3» ( для Условий 1 (начало), 2 (начало) и 3 ) доказана.
*********
Часть вторая (Утверждения3)
Возможны случаи: либо  , либо
, либо  .
.
(Об «Исключении» из общего правила)
Доказательство
Казалось бы, мы должны рассмотреть еще моменты в Условиях 1 и 2, когда перед скобками в (12), …, (15) стоят разные знаки (как при доказательстве «Утверждения 2» в части 2). Интуиция подсказывает, что э та процедура опять нас приведет к известным значениям b и c: либо  (из
(из 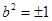 ), либо
), либо  (из
(из  ), либо b и c – четные, чего не должно быть, либо b и c не являются целыми числами (подобно доказательству части 2 «Утверждения 2»).
), либо b и c – четные, чего не должно быть, либо b и c не являются целыми числами (подобно доказательству части 2 «Утверждения 2»).
Для подтверждения сказанного рассмотрим подробно только часть Условия 1.
Итак, осталось рассмотреть случаи, когда перед скобками стоят разные знаки.
Случай 1.
 (12)
(12)
 (13′)
(13′)
 (14)
(14)
 (15), которые также являются решениями уравнения
(15), которые также являются решениями уравнения
(11)  .
.
Тогда сумма  имеет вид:
имеет вид:

Учитывая (10) и (15), можно получить разность  :
:


 =>
=>  .
.
Выразим из (17) и (16)  :
:
 =>
=> 
 =>
=>  .
.
По условию  должны быть взаимно простыми целыми числами, поэтому их общий множитель
должны быть взаимно простыми целыми числами, поэтому их общий множитель  .
.
Т.о.,  имеют вид:
имеют вид:
 ,
,  , а их сумма
, а их сумма  .
.
Т.к. из (4) c2 + b2 = 2 β, то 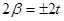 =>
=>  .
.
Из (15) с учетом (20) выразим  :
:
 , т.е.
, т.е.  .
.
Т.о.,  ,
,  , т.е.
, т.е.

 ,
,
выражения которых, с учетом (24), полностью совпадают с (6) и (7), т.е. с уравнениями

Теперь, с учетом (13′) и (14), найдем сумму  :
:
 т.к.
т.к.  , т.е.
, т.е.  .
.
(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (20). В последующих действиях мы это учтем.)
Теперь, учитывая (23), получим значение для b2:
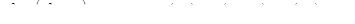 , т.к. из (20) получается
, т.к. из (20) получается
 (20′).
(20′).
Итак,  (28), что для целых чисел неприемлемо.
(28), что для целых чисел неприемлемо.
 2020-01-14
2020-01-14 127
127








