Аналитическая геометрия
Методическая разработка для самостоятельной
работы студентов по курсу «Высшая математика»
Магнитогорск
2007
Составитель: Акуленко И. В.
Аналитическая геометрия: Методическая разработка для самостоятельной работы студентов по курсу «Высшая математика» для студентов всех специальностей. Магнитогорск: МГТУ, 2007. 30 с.
Методическая разработка содержит перечень вопросов по изучаемому разделу, решение типовых задач по изучаемому разделу.
Рецензент: старший преподаватель Коротецкая В. А.
Введение
Методическая разработка предназначена для студентов всех специальностей.
Данная методическая разработка ставит своей целью помочь студенту самостоятельно овладеть методами решения задач по разделу «Аналитическая геометрия».
В методической разработке:
· содержится теоретическое введение;
· решение типовых задач;
· указана литература.
Методическая разработка предоставляет студенту широкие возможности для активной самостоятельной работы.
Прямая на плоскости
1) 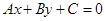 – общее уравнение прямой;
– общее уравнение прямой;
2) 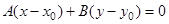 – уравнение прямой, проходящей через точку М0(х0, у0) перпендикулярно нормальному вектору
– уравнение прямой, проходящей через точку М0(х0, у0) перпендикулярно нормальному вектору 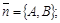
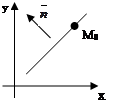

3) 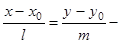 уравнение прямой, проходящей через точку М0(х0, у0) параллельно направляющему вектору
уравнение прямой, проходящей через точку М0(х0, у0) параллельно направляющему вектору 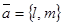 (каноническое уравнение прямой);
(каноническое уравнение прямой);
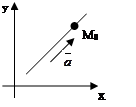
4) 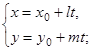
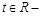 параметрическое уравнение прямой;
параметрическое уравнение прямой;
5) 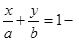 уравнение прямой в отрезках, где
уравнение прямой в отрезках, где 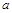 и
и 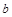 - величины направленных отрезков, отсекаемых на координатных осях
- величины направленных отрезков, отсекаемых на координатных осях 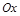 и
и 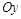 соответственно;
соответственно;
6) 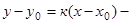 уравнение прямой, проходящей через точку М0(х0, у0),
уравнение прямой, проходящей через точку М0(х0, у0), 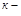 угловой коэффициент прямой, равный тангенсу угла наклона прямой к положительному направлению оси
угловой коэффициент прямой, равный тангенсу угла наклона прямой к положительному направлению оси 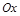 ;
;
7) 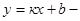 уравнение прямой с угловым коэффициентом
уравнение прямой с угловым коэффициентом 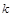 ;
; 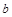 - величина отрезка, отсекаемого прямой на оси
- величина отрезка, отсекаемого прямой на оси 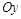 ;
;
8) 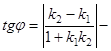 тангенс острого угла между двумя прямыми
тангенс острого угла между двумя прямыми 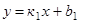 и
и 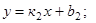

9) 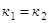 и
и  условия параллельности и перпендикулярности двух прямых
условия параллельности и перпендикулярности двух прямых 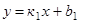 и
и 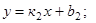

10) 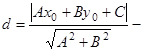 расстояние от точки М0(х0, у0) до прямой
расстояние от точки М0(х0, у0) до прямой 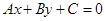 ;
;
11) 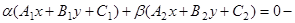 уравнение пучка прямых, проходящих через точку пересечения прямых
уравнение пучка прямых, проходящих через точку пересечения прямых 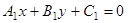 и
и 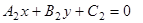
12) 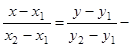 уравнение прямой, проходящей через две данные точки М1(х1, у1) и М2(х2, у2);
уравнение прямой, проходящей через две данные точки М1(х1, у1) и М2(х2, у2);
Пример 1. Даны вершины треугольника М1(2; 1), М2(-1; -1) и М3(3; 4). Составить уравнения его высот.
Решение.
Пусть М1N – высота треугольника М1М2М3. Рассмотрим два вектора 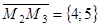 и
и 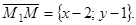 По условию эти векторы ортогональны.
По условию эти векторы ортогональны.
Значит, 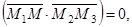
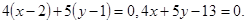 Аналогично находим другие высоты треугольника.
Аналогично находим другие высоты треугольника.
Ответ: 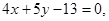
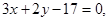
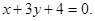
Пример 2. Составить уравнения сторон и медиан треугольника с вершинами А(3; 2), В(5; -2), С(1; 0).
Решение.
1) Воспользуемся уравнением прямой, 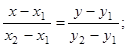
АВ: 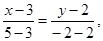
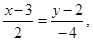
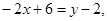
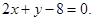
Найдем уравнение медианы АМ. Для этого найдем координаты точки М – середины отрезка ВС:
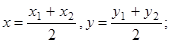
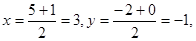
М(3; -1).
Уравнение АМ: 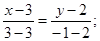
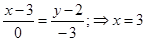
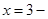 уравнение медианы, проведенной из вершины А.
уравнение медианы, проведенной из вершины А.
2) Найдем уравнения СВ и CN; N(x; y), где 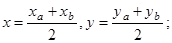
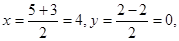 N(4; 0).
N(4; 0).
Тогда ВС: 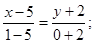
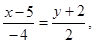
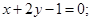
CN: 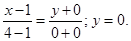
Ответ: АВ: 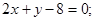 ВС:
ВС: 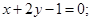 СА:
СА: 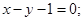 АМ:
АМ: 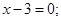
СN: 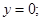 BF:
BF: 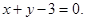
Пример 3. Даны вершины треугольника А(1; -1), В(-2; 1) и С(3;5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану, проведенную из вершины В.
Решение.
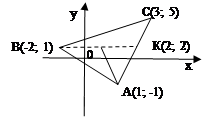 |
По условию 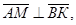 следовательно,
следовательно, 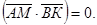
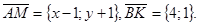
Тогда искомое уравнение будет: 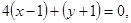
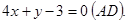
Ответ: 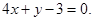
Пример 4. Составить уравнения сторон треугольника, зная одну из его вершин В(2;-7), а также уравнение высоты 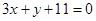 и медианы
и медианы 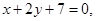 проведенных из различных вершин.
проведенных из различных вершин.
Решение.
1) По условию 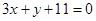 есть уравнение высоты треугольника, значит, её нормальный вектор
есть уравнение высоты треугольника, значит, её нормальный вектор 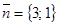 является направляющим вектором стороны ВС.
является направляющим вектором стороны ВС.
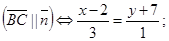
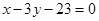 (ВС).
(ВС).
2) Обозначим координаты вершины А через x1, y1: A(x1; y1). Так как точка М(х; у) середина отрезка АВ, то 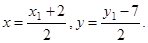 Так как точка М(х; у) лежит на медиане, то её координаты удовлетворяют уравнению
Так как точка М(х; у) лежит на медиане, то её координаты удовлетворяют уравнению 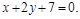 Кроме того, точка А лежит на высоте h:
Кроме того, точка А лежит на высоте h: 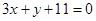 , значит, координаты точки A(x1; y1) удовлетворяют этому уравнению. Получаем линейную алгебраическую систему двух уравнений с двумя неизвестными:
, значит, координаты точки A(x1; y1) удовлетворяют этому уравнению. Получаем линейную алгебраическую систему двух уравнений с двумя неизвестными:
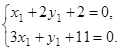
Отсюда находим х1=-4, у1=1, А(-4; 1).
3) Найдем уравнение стороны АВ треугольника как уравнение прямой, проходящей через В(2; -7) параллельно вектору 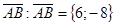
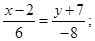
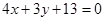 (АВ).
(АВ).
4) Найдем координаты вершины С как точки пересечения прямых (ВС) и (m):
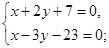 отсюда С(5; -6).
отсюда С(5; -6).
5) Уравнение стороны АС как уравнение прямой, проходящей через две данные точки: А(-4; 1) и С(5; -6); 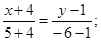
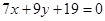 (АС).
(АС).
Ответ: (ВС) 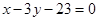 , (АВ)
, (АВ) 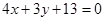 ,
,
(АС) 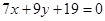 .
.
Пример 5. Составить уравнение биссектрис углов между прямыми 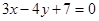
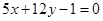 .
.
Решение.
Точка М(х, у) лежит на одной из биссектрис углов, образованных данными прямыми тогда и только тогда, когда расстояние d1 и d2 от этой точки М до данных прямых равны между собой: d1=d2 , т.е.
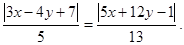
Значит, уравнение одной из биссектрис имеет вид: 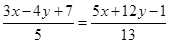 , а уравнение другой
, а уравнение другой 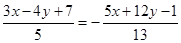 или
или 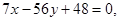
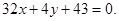
Ответ: 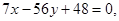
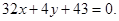
Пример 6. Составить уравнение биссектрисы того угла между двумя прямыми 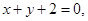
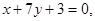 в котором лежит точка А(2; -1).
в котором лежит точка А(2; -1).
Решение.
Подставляя координаты точки А в левые части уравнения прямых, получим 2+7(-1)+3<0, 2-1+2>0. Значит, точка А лежит в тех полуплоскостях от данных прямых, для координат точек которых 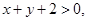
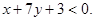 Искомая биссектриса проходит, следовательно, в тех областях, для координат точек которых функции
Искомая биссектриса проходит, следовательно, в тех областях, для координат точек которых функции 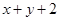 и
и 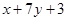 имеют разные знаки. Значит, уравнение искомой биссектрисы:
имеют разные знаки. Значит, уравнение искомой биссектрисы: 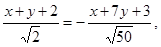 или
или 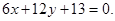
Ответ: 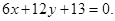
Плоскость
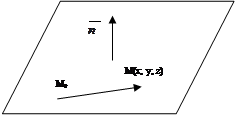
1) 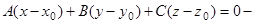 уравнение плоскости, проходящей через точку
уравнение плоскости, проходящей через точку 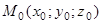 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 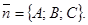
 |
2) 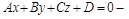 общее уравнение плоскости,
общее уравнение плоскости, 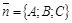 - нормальный вектор этой плоскости.
- нормальный вектор этой плоскости.
3) 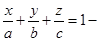 уравнение плоскости в отрезках, где a, b, c – величины направленных отрезков, отсекаемых плоскостью
уравнение плоскости в отрезках, где a, b, c – величины направленных отрезков, отсекаемых плоскостью 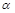 на координатных осях Ох, Оу, Оz соответственно;
на координатных осях Ох, Оу, Оz соответственно;
4) Пусть даны две плоскости 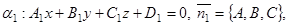
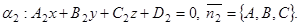
В качестве угла 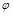 между плоскостями
между плоскостями 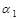 и
и 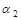 принимается угол между их нормальными векторами:
принимается угол между их нормальными векторами: 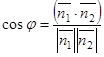 или в координатной форме
или в координатной форме
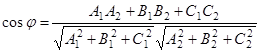
5) Условие перпендикулярности двух плоскостей 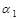 и
и 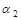 :
: 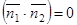 или в координатной форме:
или в координатной форме: 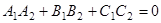 .
.
6) Условие параллельности двух плоскостей 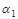 и
и 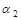 :
: 
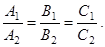
7) Уравнение плоскости, проходящей через три данные точки:
М1(х1; y1; z1), М2(х2; y2; z2), М3(х3; y3; z3):
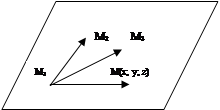 |
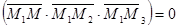 или в координатной форме:
или в координатной форме: 
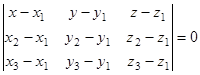
8) Если плоскость 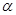 задана общим уравнением
задана общим уравнением 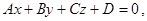 а
а 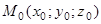 - некоторая точка пространства, то
- некоторая точка пространства, то 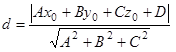 есть формула расстояния от точки М0 до плоскости
есть формула расстояния от точки М0 до плоскости 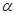 .
.
9) Совокупность всех плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей.
Если 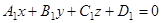 и
и 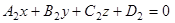 есть уравнения двух различных непараллельных плоскостей, пересечением которых служит некоторая прямая L, а числа
есть уравнения двух различных непараллельных плоскостей, пересечением которых служит некоторая прямая L, а числа 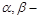 любые не равные одновременно нулю, то
любые не равные одновременно нулю, то 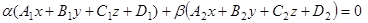 есть уравнение плоскости, проходящей через прямую L. Более того, какова бы ни была проходящая через прямую L плоскость, она может быть определена из пучка плоскостей при определенных значениях
есть уравнение плоскости, проходящей через прямую L. Более того, какова бы ни была проходящая через прямую L плоскость, она может быть определена из пучка плоскостей при определенных значениях 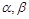 .
.
Пример 1. Составить уравнение плоскости, которая проходит через точку М1(2; 1; -1) и имеет нормальный вектор 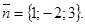
Решение.
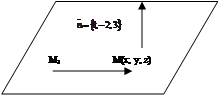 |
Для вывода уравнения плоскости возьмем на этой плоскости точку М(x; y; z) с текущими координатами. Получим вектор 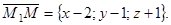
По условию 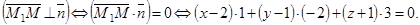
Ответ: 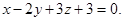
Пример 2. Даны две точки М1(3; -1; 2) М2(4; -2; -1). Составить уравнение плоскости, проходящей через М1 перпендикулярно вектору 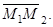
Решение.
По условию вектор 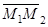 является нормальным вектором искомой плоскости
является нормальным вектором искомой плоскости 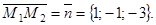 Уравнение плоскости, проходящей через точку М1 перпендикулярно вектору
Уравнение плоскости, проходящей через точку М1 перпендикулярно вектору 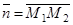 есть
есть 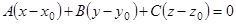 или
или
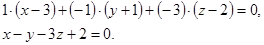
Ответ: 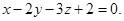
Пример 3. Составить уравнение плоскости, проходящей через точку М1(3; 4; -5) параллельно двум векторам 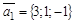 и
и 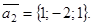
Решение.
Отложим векторы 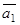 и
и 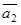 в плоскости, проходящей через точку М1, и возьмем на искомой плоскости точку М(x; y; z) с текущими координатами.
в плоскости, проходящей через точку М1, и возьмем на искомой плоскости точку М(x; y; z) с текущими координатами.
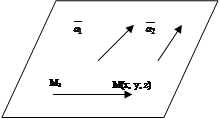 |
Получим, что три вектора 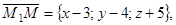
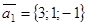 ,
, 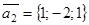 лежат в одной плоскости, т.е. они компланарны.
лежат в одной плоскости, т.е. они компланарны.
Условие компланарности есть равенство нулю определителя, составленного из координат этих векторов.
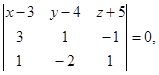
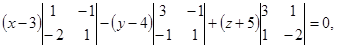
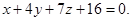
Ответ: 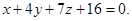
Пример 4. Составить уравнение плоскости, проходящей через точку М1(2; -1; 3) и М2(3; 1; 2) параллельно вектору 
Решение.
Отложим вектор 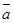 и точку М(x; y; z) с текущими координатами в плоскости, проходящей через точки М1 и М2.
и точку М(x; y; z) с текущими координатами в плоскости, проходящей через точки М1 и М2.
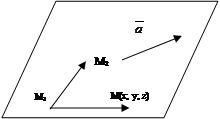 |
Получим компланарные векторы 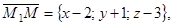
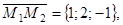
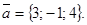 Следовательно, по условию компланарности трех векторов будем иметь:
Следовательно, по условию компланарности трех векторов будем иметь:
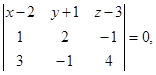 или
или 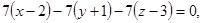
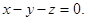
Ответ: 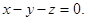
Пример 5. Составить уравнение плоскости, проходящей через три точку М1(3; -1; 2), М2(4; -1; -1) и М3(2; 0; 2).
Решение.
Возьмем на плоскости точку с текущими координатами М(x; y; z), будем иметь векторы 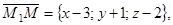
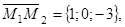
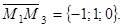
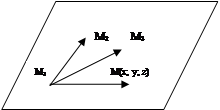 |
Эти векторы по условию компланарны. Условие компланарности есть равенство нулю определителя, составленного из координат этих векторов:
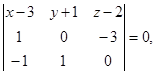 или
или 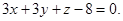
Ответ: 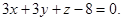
Пример 6. Составить уравнение плоскости, проходящей через точку М1(3; -2; 7) параллельно плоскости 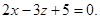
Решение.
Так как искомая плоскость и данная – параллельны, то у них общий нормальный вектор. Таким образом, получим: через данную точку М1 провести плоскость, перпендикулярно данному вектору 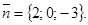
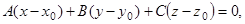
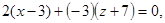
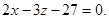
Ответ: 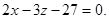
Пример 7. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям: 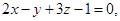
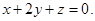
Решение.
Так как искомая плоскость перпендикулярна плоскостям 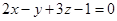 и
и 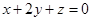 , то нормальные векторы
, то нормальные векторы 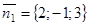 и
и 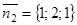 и вектор
и вектор 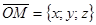 (М – точка с текущими координатами) – компланарны. Следовательно,
(М – точка с текущими координатами) – компланарны. Следовательно, 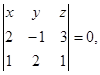 или
или 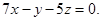
Ответ: 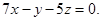
Пример 8. Составить уравнение плоскости, проходящей через две точки М1(1; -1; -2) и М2(3; 1; 1) перпендикулярно к плоскости 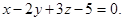
Решение.
Так как искомая плоскость перпендикулярна плоскости 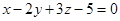 , то нормальный вектор
, то нормальный вектор 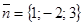 отложим в плоскости точек М1 и М2.
отложим в плоскости точек М1 и М2.
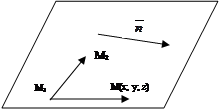 |
Возьмем на искомой плоскости ещё точку с текущими координатами, получим векторы: 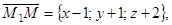
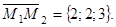
Три вектора 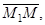
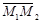 и
и 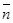 - компланарны, поэтому
- компланарны, поэтому 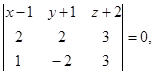 или
или 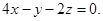
Ответ: 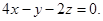
Пример 9. Составить уравнение плоскости, которая проходит через ось Оу и точку М2(1; 4; 3).
Решение.
Так как плоскость проходит через ось Оу, то её уравнение можно взять в виде 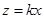 . Плоскость
. Плоскость 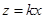 проходит через точку М2(1; 4; 3), значит, координаты точки удовлетворяют уравнению. Получаем:
проходит через точку М2(1; 4; 3), значит, координаты точки удовлетворяют уравнению. Получаем: 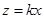 ,
, 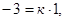 к =-3,
к =-3, 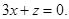
Ответ: 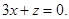
Пример 10. Составить уравнение плоскости, проходящей через точки М1(7; 2; -3) и М2(5; 6; -4) параллельно оси Ох.
Решение.
Уравнение плоскости, параллельной оси Ох, имеет вид: 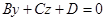 (коэффициенты B, C, D отличны от нуля). Запишем это уравнение так:
(коэффициенты B, C, D отличны от нуля). Запишем это уравнение так: 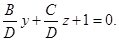 Так как эта плоскость проходит через точки М1 и М2, то координаты этих точек удовлетворяют искомому уравнению, получаем линейную алгебраическую систему уравнений:
Так как эта плоскость проходит через точки М1 и М2, то координаты этих точек удовлетворяют искомому уравнению, получаем линейную алгебраическую систему уравнений:
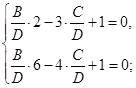 Þ
Þ 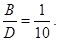
Тогда 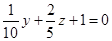 или
или 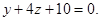
Ответ: 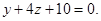
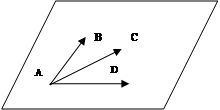
Пример 11. Докажите, что четыре точки А(1; 2; -1), В(0; 1; 5), С(-1; 2; 1), D(2; 1; 3) лежат в одной плоскости.
Решение.
Рассмотрим векторы 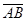 ,
, 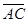 ,
, 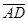 .Если они компланарны, то данные точки лежат в одной плоскости.
.Если они компланарны, то данные точки лежат в одной плоскости.
 |
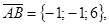
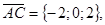
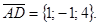
Тогда 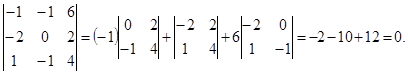
Ответ: данные точки лежат в одной плоскости.
Пример 12. Составить уравнение плоскости, которая проходит через точку М1(4; 3; 2) и отсекает на координатных осях положительные отрезки одинаковой длины.
Решение.
Уравнение плоскости в отрезках: 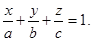 По условию а=b=c> 0. Тогда уравнение плоскости можно записать
По условию а=b=c> 0. Тогда уравнение плоскости можно записать 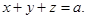 Так как точка М1(4; 3; 2) лежит в этой плоскости, то её координаты удовлетворяют уравнению: 4+3+2= а, а =9. Следовательно,
Так как точка М1(4; 3; 2) лежит в этой плоскости, то её координаты удовлетворяют уравнению: 4+3+2= а, а =9. Следовательно, 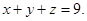
Ответ: 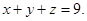
Пример 13. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 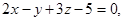
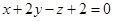 параллельно вектору
параллельно вектору 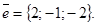
Решение.
Векторы 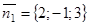 и
и 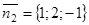 - нормальные векторы данных плоскостей.
- нормальные векторы данных плоскостей.
Найдем их векторное произведение:
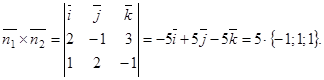
В качестве направляющего вектора прямой пересечения плоскостей примем вектор 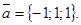
Возьмем какую – нибудь точку на этой прямой, например, М1(х; у; 0), тогда

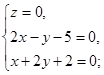
 Û М1(
Û М1(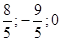 ).
).
Так как векторы 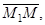
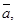
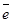 компланарны, то
компланарны, то 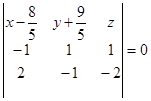 Þ
Þ 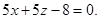
Ответ: 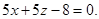
Прямая и плоскость в пространстве
1) 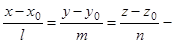 каноническое уравнение прямой, проходящей через точку М0(x0; y0; z0) параллельно направляющему вектору
каноническое уравнение прямой, проходящей через точку М0(x0; y0; z0) параллельно направляющему вектору 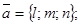
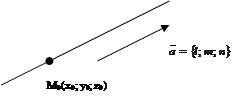
2) 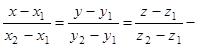 уравнение прямой, проходящей через две данные точки М1(x1; y1; z1) и М2(x2; y2; z2);
уравнение прямой, проходящей через две данные точки М1(x1; y1; z1) и М2(x2; y2; z2);
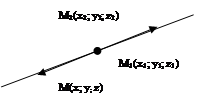
3) уравнения 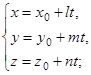
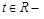 параметрическое уравнение прямой в пространстве.
параметрическое уравнение прямой в пространстве.
4) Пусть даны две прямые, заданные каноническими уравнениями
L1: 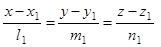 ,
,
L2: 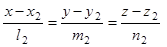 .
.
За угол φ между прямыми принимают угол между их направляющими векторами 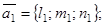
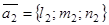 :
:
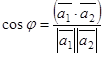 , или в координатной форме
, или в координатной форме
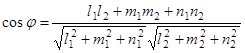 .
.
5) 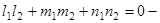 условие перпендикулярности двух прямых L1 и L2.
условие перпендикулярности двух прямых L1 и L2.
6) 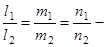 условие параллельности двух прямых L1 и L2 в пространстве.
условие параллельности двух прямых L1 и L2 в пространстве.
7) Общие уравнения прямой в пространстве
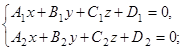
где коэффициенты А1, В1, С1 не пропорциональны коэффициентам А2, В2, С2. В данном случае прямая задана как линия пересечения плоскостей.
Пример 1. Найти уравнение плоскости, проходящей через прямые:
L1: 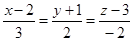 , L2:
, L2: 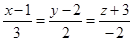 .
.
Решение.
Обозначим точки, через которые проходят прямые L1 и L2 - М1(2; -1; 3) и М2(1; 2; -3). Им соответствует вектор 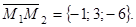
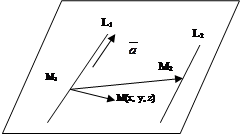 |
Возьмем на искомой плоскости точку М(x; y; z) с текущими координатами, получим вектор 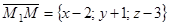 . Таким образом, три вектора
. Таким образом, три вектора 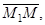
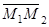 и направляющий вектор прямой
и направляющий вектор прямой
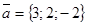 компланарны. По условию компланарности трех векторов имеем
компланарны. По условию компланарности трех векторов имеем 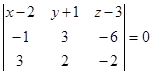 или
или 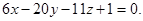
Ответ: 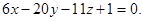
Пример 2. Составить уравнение плоскости, проходящей через прямую 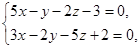 перпендикулярно плоскости
перпендикулярно плоскости 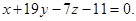
Решение.
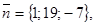
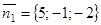 ,
, 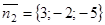 . Данная прямая действительно перпендикулярна данной плоскости:
. Данная прямая действительно перпендикулярна данной плоскости:
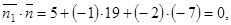
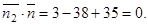
Следовательно, по условию задачи будут удовлетворять все плоскости, принадлежащие пучку плоскостей, проходящих через эту прямую.
Ответ: 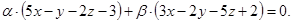
Пример 3. Составить уравнение плоскости, проходящей через точку М1(1; 2; -3) параллельно прямым 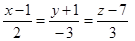 ,
, 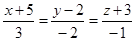 .
.
Решение.
Отложим в искомой плоскости точки М1(1; 2; -3), М(x; y; z) и векторы 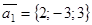 ,
, 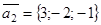 .
.
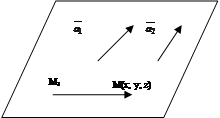
Тогда три вектора 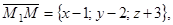
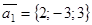 и
и 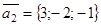 будут компланарны. По условию компланарности трех векторов будем иметь:
будут компланарны. По условию компланарности трех векторов будем иметь: 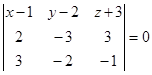 , т.е.
, т.е.
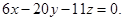
Ответ: 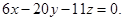
Пример 4. Составить параметрические уравнения прямой, проходящей через точку М1(1; -1; -3) параллельно прямой 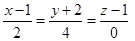 .
.
Решение.
Возьмем на искомой прямой точку М(x; y; z) с текущими координатами, тогда векторы 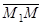 и
и 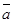 будут коллинеарные, т.е.
будут коллинеарные, т.е. 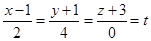 . Отсюда получаем
. Отсюда получаем 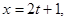
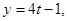
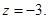
Ответ: 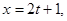
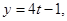
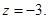
Пример 5. Составить уравнение плоскости, проходящей через точку М1(2; -2; 1) и прямую 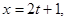
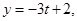
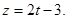
Решение.
По уравнениям данной прямой находим точку прямой М2(1; 2; -3) и направляющий вектор прямой 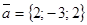 .
.
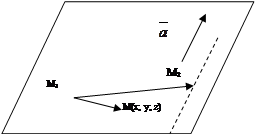 |
Получаем три вектора, отложенных в искомой плоскости: 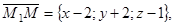
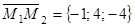 ,
, 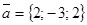 .
.
По условию компланарности трех векторов имеем:
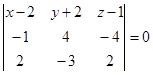 или
или 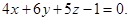
Ответ: 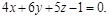
Пример 6. Составить уравнение плоскости, проходящей через прямую 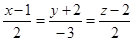 перпендикулярно к плоскости
перпендикулярно к плоскости 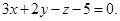
Решение.
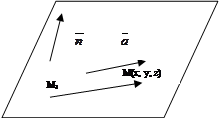 |
Три вектора 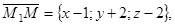
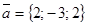 ,
, 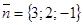 компланарны только тогда, когда
компланарны только тогда, когда 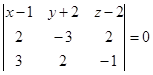 или
или 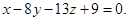
Ответ: 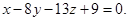
Пример 7. Составить уравнение плоскости, проходящей через точку М1(1; -2; 1) перпендикулярно прямой 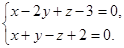
Решение.
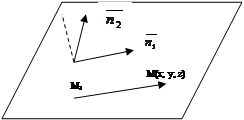 |
Так как искомая плоскость перпендикулярна прямой, заданной общими уравнениями, то нормальные векторы данных плоскостей можно отложить вместе с вектором 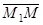 в одной плоскости. Следовательно, векторы
в одной плоскости. Следовательно, векторы 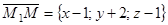 ,
, 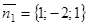 ,
, 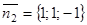 компланарны. По условию компланарности трех векторов имеем:
компланарны. По условию компланарности трех векторов имеем:
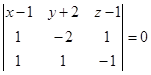 или
или 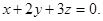
Ответ: 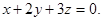
Пример 8. Составить уравнение плоскости, проходящей через точку М1(1; 1; -1) и М2(3; 4; 1) параллельно прямой 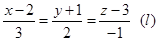 .
.
Решение.
Возьмем на искомой плоскости точку с текущими координатами, получим вектор 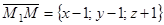 .
.
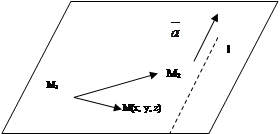 |
Векторы 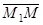 ,
, 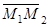 , и
, и 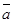 компланарны. По условию компланарности трех векторов
компланарны. По условию компланарности трех векторов 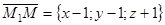 ,
, 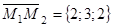 ,
, 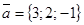 имеем:
имеем:
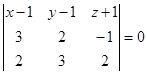 или
или 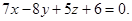
Ответ: 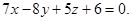
Пример 9. Составить уравнение перпендикуляра, опущенного из точки М0(2; 3; 1) на плоскость 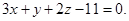
Решение.
Нормальный вектор 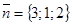 данной плоскости будет по условию направляющим вектором прямой, проходящей через точку М0(2; 3; 1). Её уравнение
данной плоскости будет по условию направляющим вектором прямой, проходящей через точку М0(2; 3; 1). Её уравнение 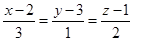
Ответ: 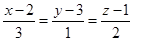 .
.
Пример 10. Составить уравнение перпендикуляра, опущенного из точки М1(3; 2; 1) на прямую 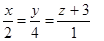 .
.
Решение.
1) Составим уравнение плоскости, проходящей через данную точку М1(3; 2; 1) перпендикулярно данной прямой (или перпендикулярно вектору 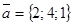 - направляющему вектору прямой):
- направляющему вектору прямой):
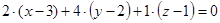 или
или 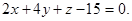
2) Составим уравнение плоскости, проходящей через данную точку и данную прямую. На данной прямой возьмем точку М2(0; 0; -3). Тогда надо найти вторую плоскость, проходящую через точки М1(3; 2; 1) и М2(0; 0; -3), и параллельно направляющему вектору данной прямой 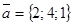 . Имеем
. Имеем 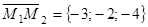 . Следовательно, уравнение второй плоскости
. Следовательно, уравнение второй плоскости
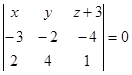 или
или 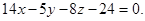
Найденные плоскости пересекаются по прямой l, которая проходит через данную точку и перпендикулярна данной прямой, поэтому уравнения 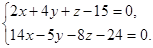 и будут уравнениями прямой l – искомого перпендикуляра.
и будут уравнениями прямой l – искомого перпендикуляра.
Ответ: 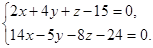
Пример 11. Написать уравнение прямой, проходящей через точку М0(-4; 3; 0) и параллельно прямой 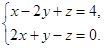
Решение.
Найдем направляющий вектор прямой 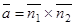 ,
,
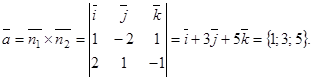 Тогда уравнение искомой прямой есть
Тогда уравнение искомой прямой есть 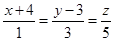 .
.
Ответ: 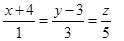 .
.
Пример 12. Найти прямую, проходящую через точку М0(-4; 3; 0) и перпендикулярно к прямым 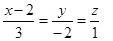 и
и 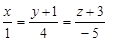 .
.
Решение.
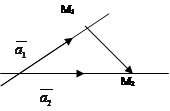 |
Вычислим направляющий вектор перпендикуляра к плоскости, проходящей через прямую параллельно другой прямой.
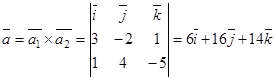
Тогда уравнение искомого перпендикуляра будет: 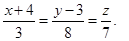
Ответ: 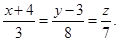
Пример 13. Задана плоскость Р: 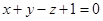 и прямая L:
и прямая L: 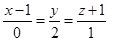 , причем LÎР.
, причем LÎР.
Требуется найти:
a) угол между прямой и плоскостью;
b) координаты точек пересечения прямой и плоскости.
Решение.
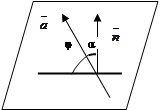
a) 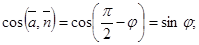
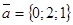 ,
, 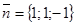 ,
, 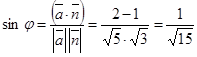 ,
,
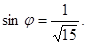
b) Найдем точку пересечения прямой и плоскости.
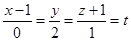 , или параметрически х =1, у =2t, z =t-1.
, или параметрически х =1, у =2t, z =t-1.
Подставим параметрические уравнения прямой в уравнение плоскости, найдем значение t: 1+2t-t+1+1=0; t=-3. Тогда координаты точки пересечения прямой и плоскости будут: х =1, у =-6, z =-4.
Ответ: а) 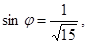 b) (1; -6; -4).
b) (1; -6; -4).
Пример 14. Определить косинус угла между прямыми: 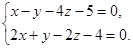
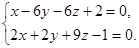
Решение.
Найдем направляющие векторы данных прямых
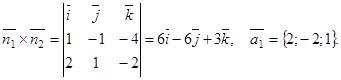
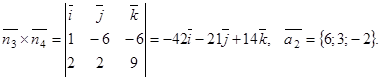
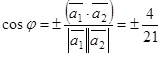 ,
, 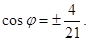
Ответ: 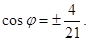
Пример 15. Найти проекцию точки А(4; -3; 1) на плоскость 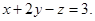
Решение.
8) Найдем уравнение перпендикуляра, проходящего через точку А(4; -3; 1), к плоскости 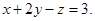
Получим 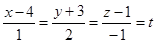 .
.
9) Найдем точку пересечения прямой и данной плоскости. Для этого подставим х =t+4, у =2t, z =-t+1 в уравнение плоскости. Будем иметь уравнение относительно параметра t: t+4+2(2t-3)-(t+1)-3=0; 6t=6; t=1.
10) Подставим найденное значение параметра t=1 в параметрическое уравнение прямой, получим х0=5, у0=-1, z0=0.
Ответ: (5; -1; 0).
Пример 16. Найти расстояние от точки М(2; -1; 3) до прямой 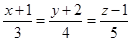 .
.
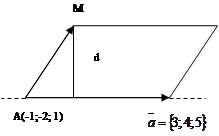 Решение.
Решение.
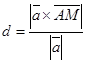 ; найдем
; найдем 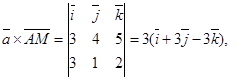
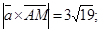
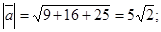
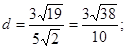
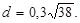
Ответ: 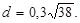
Пример 17. Заданы скрещивающиеся прямые L1: 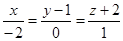 и
и
L2: 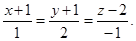 Найти расстояние d (L1; L2) между прямыми и написать уравнение общего перпендикуляра L к этим прямым.
Найти расстояние d (L1; L2) между прямыми и написать уравнение общего перпендикуляра L к этим прямым.
Решение.
 |
Найдем уравнение плоскости Р, проходящей через прямую L1, параллельную L2. Точка М1(0; 1; -2) лежит на прямой L1 и, следовательно, принадлежит искомой плоско
|
|
 2020-01-14
2020-01-14 112
112






