Цель работы: исследовать параметры нелинейных стационарных объектов, описываемых системами нелинейных алгебраических уравнений, используя для их решения средства пакета MathCAD.
Содержание работы:
1) изучить теоретические положения (раздел 2.1), раскрывающие структуру нелинейных стационарных объектов, их математическое описание и пример решения систем нелинейных алгебраических уравнений средствами пакета MathCAD, используемый для анализа такого рода объектов;
2) выполнить индивидуальное задание согласно предусмотренной в разд.2.2 последовательности выполнения работы;
3) оформить описание раздела по контрольной работе согласно требованиям задания.
Краткие теоретические сведения
Структура и математическая модель объекта
Структурная схема нелинейного стационарного объекта имеет вид:
| ||||
| ||||
|

Такой объект представляет собой систему, которая имеет два входа х1 и х2 с постоянными значениями в установившемся режиме и два выхода в1 и в2. Структура объекта определяется сумматором S1 , умножителем М1, двумя линейно– усилительными блоками а1 , а2 и системой связей между ними.
В отличие от линейных стационарных объектов нелинейные описываются системами нелинейных алгебраических уравнений.
 Математическая модель, соответствующая такой схеме, имеет вид:
Математическая модель, соответствующая такой схеме, имеет вид:
а1х1 +а2х2=в1;
х1х2=в2
2.1.2. Анализ объектов
Исследование такого рода объектов состоит в определении значений входных воздействий х1 ,х2 в зависимости от значений выходов в1 и в2 при заданных параметрах объекта а1 и а2 .
Реализация решения задачи исследования нелинейного стационарного объекта в такой постановке может быть осуществлена с помощью средств системы символьной математики MathCAD 7.0 PRO.
2.1.3. Решение нелинейных алгебраических и трансцендентных уравнений
2.1.3.1. Постановка задачи. Пусть дано уравнение
 , (2.1)
, (2.1)
где функция  определена и непрерывна на некотором интервале (А,В). Всякое значение
определена и непрерывна на некотором интервале (А,В). Всякое значение  , обращающее функцию
, обращающее функцию  в нуль, то есть такое, при котором
в нуль, то есть такое, при котором 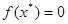 , называется корнем уравнения (2.1), а процесс нахождения
, называется корнем уравнения (2.1), а процесс нахождения  называется его решением.
называется его решением.
Если функция  представляет собой многочлен относительно
представляет собой многочлен относительно  , то уравнение называется нелинейным алгебраическим (например,
, то уравнение называется нелинейным алгебраическим (например,  ); если в функцию
); если в функцию  входят элементарные (тригонометрические, логарифмические, показательные и т.п.) функции, то такое уравнение называется трансцендентным (например,
входят элементарные (тригонометрические, логарифмические, показательные и т.п.) функции, то такое уравнение называется трансцендентным (например,  ).
).
2.1.3.2. Характеристика методов. Методы решения нелинейных алгебраических и трансцендентных уравнений (НАТУ) делятся на прямые и итерационные. Первые позволяют найти решение непосредственно с помощью формул и всегда обеспечивают получение точного решения. Однако прямые методы имеются только для ограниченного круга уравнений, поэтому на практике более широко используются итерационные методы.
В итерационных методах процедура решения задается в виде многократного применения некоторого алгоритма. Полученное решение всегда является приближенным, хотя может быть сколь угодно близким к точному.
В общем случае задача решается в 2 этапа:
определение приближенных значений корней уравнения;
уточнение корней до заданной степени точности с помощью одного из итерационных методов.
Для определения приближенных значений корней уравнения используются:
1) Построение графика функций  и приближенное определение точек, где кривая пересекает ось Х.
и приближенное определение точек, где кривая пересекает ось Х.
Запись уравнения  в виде
в виде 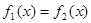 и построение графиков двух функций:
и построение графиков двух функций:  и
и  . Точка их пересечения и есть корень исходного уравнения (5.1).
. Точка их пересечения и есть корень исходного уравнения (5.1).
На втором этапе происходит уточнение корня с использованием критерия окончания итерационного процесса.
Итерационный процесс следует оканчивать, когда  <
<  , т.е. при близости двух последовательных приближений к корню.
, т.е. при близости двух последовательных приближений к корню.
Одним из итерационных методов для уточнения корня является метод Ньютона.
2.1.3.3.Метод Ньютона
2.1.3.3.1. Геометрическая интерпретация метода Ньютона. Геометрическая интерпретация метода Ньютона показана на рис 2.1.

Рис. 2.1. Метод Ньютона
Приняв в качестве начального приближения к корню  некоторое значение
некоторое значение  , восстанавливаем перпендикуляр в точке
, восстанавливаем перпендикуляр в точке  к оси Х. В точке пересечения перпендикуляра с графиком функции
к оси Х. В точке пересечения перпендикуляра с графиком функции 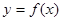 , для которой отыскивается нуль, проводим касательную к кривой. Точка пересечения касательной с осью Х дает новое приближение
, для которой отыскивается нуль, проводим касательную к кривой. Точка пересечения касательной с осью Х дает новое приближение  к корню. После этого процесс повторяем для точки
к корню. После этого процесс повторяем для точки  , получаем точку
, получаем точку  и т.д.
и т.д.
2.1.3.3.2. Получение формулы Ньютона. Определим рекуррентное соотношение для нахождения корня методом Ньютона.
Уравнение касательной в точке  можно получить как уравнение прямой, проходящей через заданную точку
можно получить как уравнение прямой, проходящей через заданную точку  и имеющей угловой коэффициент
и имеющей угловой коэффициент  :
:

В точке  пересечения касательной с осью Х, величина
пересечения касательной с осью Х, величина  равняется нулю:
равняется нулю:

Отсюда

В общем случае для вычисления последующего приближения  к корню по известному предыдущему
к корню по известному предыдущему 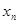 формула Ньютона имеет вид:
формула Ньютона имеет вид:

К такому же результату можно придти, используя разложение в ряд Тейлора:

Члены, содержащие  во второй и более высоких степенях, отбрасываются; используется соотношение
во второй и более высоких степенях, отбрасываются; используется соотношение  . Предполагается, что переход от
. Предполагается, что переход от  к
к  приближает значение функции к нулю так, что
приближает значение функции к нулю так, что  т.е. точка
т.е. точка  выбирается такой, что значение функции в ней равняется нулю:
выбирается такой, что значение функции в ней равняется нулю:

Полученная точка 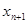 является точкой пересечения касательной в точке
является точкой пересечения касательной в точке  с осью Х. Поскольку кривая
с осью Х. Поскольку кривая  отлична от прямой, то значение функции
отлична от прямой, то значение функции  скорее всего не будет в точности равно нулю (это результат отбрасывания членов высшего порядка в ряде Тейлора). Поэтому вся процедура повторяется, причем вместо
скорее всего не будет в точности равно нулю (это результат отбрасывания членов высшего порядка в ряде Тейлора). Поэтому вся процедура повторяется, причем вместо 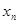 используется
используется 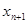 .
.
Одно из преимуществ метода Ньютона – это то, что его можно распространить на решение систем нелинейных уравнений со многими переменными.
 2020-01-14
2020-01-14 111
111








