Содержание
Введение
§1. Линейные преобразования
§2. Индексные обозначения
§3. Общее определение тензоров
§4. Скалярное произведение и метрический тензор
§5. Действия с тензорами
§6. Поднятие и опускание индексов
§7. Тензоры в криволинейных координатах
§8. Примеры вычислений
Заключение
Литература
Введение
Возникновение тензорного исчисления было подготовлено в 19 веке развитием теории алгебраических форм, с одной стороны, и теории квадратичных дифференциальных форм - с другой. Исследования в области теории дифференциальных квадратичных форм были непосредственно связаны с дифференциальной геометрией: с геометрией поверхностей (К. Гаусс) и с геометрией многомерного метрического пространства (Б. Риман). Современную форму тензорному исчислению придал итальянский математик Г. Риччи-Курбастро, поэтому тензорное исчисление иногда называется исчислением Риччи. Идеи Риччи-Курбастро первоначально не получили широкого распространения. Внимание к ним возросло после появления (1915-16) общей теории относительности А. Эйнштейна, математическая часть которой целиком основана на тензорном исчислении.
Тензор (от лат. tensus - напряжённый, натянутый), математический термин, появившийся в середине 19 века и с тех пор применяющийся в двух различных смыслах. Наибольшее распространение термин «тензор» получил в современном тензорном исчислении, где это название присваивается особого рода величинам, преобразующимся по особому закону. В механике, особенно в теории упругости, термин «тензор» широко применяется как синоним симметрического аффинора, то есть линейного оператора F, преобразующего вектор х в вектор Fх, и симметрического в том смысле, что скалярное произведение уFх не меняется при перестановке векторов х и у. Здесь термин был первоначально связан с малыми растяжениями (и сжатиями), возникающими при упругой деформации (откуда и название «тензор»), а затем перенесён в другие области механики. Так появились тензор деформации, тензор напряжения, тензор инерции и др.
Линейные преобразования
Пусть переменные 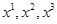 преобразуются в новые
преобразуются в новые 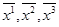 с помощью линейного преобразования
с помощью линейного преобразования
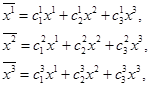
где 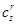 - константы (все индексы пробегают значения 1, 2, 3..., n независимо друг от друга.). Применяя условие о суммировании, можем записать эту систему уравнений в виде
- константы (все индексы пробегают значения 1, 2, 3..., n независимо друг от друга.). Применяя условие о суммировании, можем записать эту систему уравнений в виде
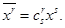 (1.1)
(1.1)
Мы предполагаем, что определитель преобразования 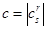 не равен нулю. Пусть
не равен нулю. Пусть 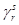 является алгебраическим дополнением элемента
является алгебраическим дополнением элемента 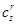 в определителе c деленным на величину
в определителе c деленным на величину 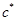 (
(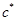 - обратная матрица). Тогда
- обратная матрица). Тогда
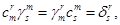 (1.2)
(1.2)
и мы можем разрешить систему уравнений (1.1) относительно x
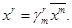 (1.3)
(1.3)
Это показывает, что данное преобразование обратимо.
Кроме того, если 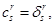 мы имеем
мы имеем
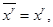
т. е. тождественное преобразование.
Если перейти сначала от переменных 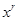 к
к 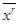 по (1.1), а затем от переменных
по (1.1), а затем от переменных 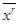 к
к 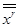 при помощи преобразования
при помощи преобразования
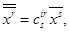
то мы видим, что переход от первоначальных переменных 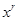 к
к 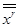 определяется формулой
определяется формулой
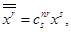
где
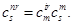
Это преобразование, следовательно, также линейное.
Говорят, что совокупность преобразований образует группу, когда она удовлетворяет следующим условиям: 1) если преобразования от 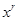 к
к 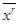 и от
и от 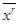 к
к 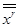 принадлежат данной совокупности, то преобразование от
принадлежат данной совокупности, то преобразование от 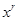 к
к 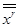 также принадлежат к ней; 2) совокупность преобразования содержит тождественное и обратное преобразования.
также принадлежат к ней; 2) совокупность преобразования содержит тождественное и обратное преобразования.
Таким образом, совокупность линейных преобразований образует группу.
 2020-01-14
2020-01-14 127
127







