При этом выполняется равенство Парсеваля

               ¥          ¥

      ò ç Ф(x)ç² dx = ò ç c(f_x)ç² df_x.                                        (2.17)

   -¥           -¥

Для функций распределения w(x) и v (p_x) имеется аналогичное соотношение нормировки

               ¥          ¥

      ò ç Ф(x)ç² dx = ò ç j(р_x)ç² dр_x = 1.                                        (2.18)

   -¥           -¥

Продолжая аналогию для сопряженных переменных х и р_х, мы можем записать

¥

  j(р_x) = ò Ф(x) exp(-2p i р_xx/h)dx/Ö h и                             (2.19)

 -¥

¥

  Ф(х) = ò j(р_x) exp(2p i р_xx/h)dр_х/Ö h,                                     (2.20)

-¥

где h – размерный коэффициент, определяемый из эксперимента. В соотношениях (2.19) и (2.20) хорошо видно, что переменная р_х/h играет такую же роль, что и пространственная частота f_x в (2.16) и (2.17), т.е. р_х аналогично hf_x = ћk_x. Теперь становится понятным соотношение, очень часто используемое в атомной физике как постулат,

 

                                 p = ћk.                                                   (2.21)

 

    Далее очень полезно вспомнить теорему о средних значениях проекций импульсов Д.И. Блохинцева с использованием преобразований Фурье [79]. Эта теорема гласит

                       ¥

              <p_xⁿ> = ò Ф*(x) (-iћ ¶/¶x)ⁿФ(x) dx,                         (2.22)

                       -¥

где < p_x > - среднее значение проекции импульса по всему конфигурационному пространству, описываемому комплексной амплитудой Ф(x) функции распределения w(x). При этом комплексная амплитуда j(p_x) функции распределения электронов по импульсам v(p_x) должна являться компонентой Фурье разложения функции Ф(x) в интеграл Фурье по пространственным частотам в форме (2.20). Последнее условие в квантовой механике постулируется, исходя из экспериментальных данных. В нашем случае это следует из теоремы Лиувилля,теории адиабатических инвариантов и показано выше.

    Таким образом, в уравнении, с помощью которого мы хотим вычислить средние значения, например, < p_x² >, величину p_x² можно заменить в соответствии с (2.22) на дифференциальный оператор согласно уравнению

 

              p_x² Ф(x) = (-iћ¶ /¶ x)²Ф(x) = - ћ² ¶²/¶x² Ф(x).            (2.23)

 

В результате такой замены задача на нахождение средних значений может быть решена полностью в конфигурационном пространстве, т.е. минуя переменные импульсов р_х.

    С использованием уравнения (2.23) закон сохранения полной энергии электрона в атоме

 

                         p²/2m + U(x,y,z,) = E                                     (2.24)

 

запишется для трех координат в виде

 

    - (ћ²/2m) DФ(x,y,z) + U(x,y,z) Ф(x,y,z) = EФ(x,y,z).            (2.25)

 

    Таким образом, мы получили стационарное уравнение Шредингера, опираясь только на теорему Лиувилля для функций распределения электронов по координатам и по импульсам, спектральный метод Фурье и закон сохранения полной энергии в атомных системах.

Это уравнение используется для вычисления стационарной электронной плотности, а также целого ряда других характеристик в атомах и молекулах. Уравнение (2.25) было постулировано Шредингером в 1926 г. на основе корпускулярно-волновых представлений де Бройля и до последнего времени не могло быть выведено в рамках квантовой теории.

При выводе статистического уравнения Шредингера (2.25) нами были использованы наиболее общие свойства движения электронов в атомных системах, т.е. движения в центральных кулоновских полях ядер, поэтому оно может быть справедливо для общего анализа различных атомных, молекулярных и других систем, где не учитываются разного рода релятивистские эффекты. С помощью данного уравнения мы можем отыскать функцию Ф(x,y,z) как комплексную амплитуду функции распределения электронов w(x,y,z) для конкретного вида потенциальной энергии U(x,y,z) и заданной полной энергии Е электрона.

Необходимо подчеркнуть еще одну особенность данной задачи. Условие нормировки (2.7) требует, чтобы функция Ф на бесконечности обращалась в нуль. Подобные ограничения на функцию называются граничными условиями, а задача с такими условиями называется краевой. Как правило, решение подобных задач сводится к отысканию собственных функций и собственных значений некоторого параметра уравнения, удовлетворяющего частному решению линейного дифференциального уравнения (задача Штурма - Лиувилля). В качестве собственных значений в данной задаче могут выступать различные интегралы движения электронов в центральных полях (полная энергия Е, модуль момента количества движения L, а также проекция механического момента на ось симметрии системы L_z).

 

2.4. Функции распределения электронов по импульсам в периодических структурах

 

Рассмотрим поведение электронов в периодической атомной структуре. Предположим, что атомы расположены в упорядоченной линейной цепочке с бесконечной протяженностью и расстояния между центрами атомов равны a (рис. П.2.1). Подобные цепочки атомов можно наблюдать в достаточно крупных совершенных монокристаллах, состоящих из однородных атомов.

Допустим также, что электроны в атомах цепочки движутся по некоторым стационарным орбитам, в результате чего устанавливается равновесное распределение электронов в пространстве. Естественно ожидать, что в данном случае распределение электронных облаков имеет пространственную периодичность с периодом, равным а.  

 

 

 

Таким образом, как функция распределения электронов по координатам w(x,y,z), так и комплексная амплитуда функции распределения Ф(x,y,z) для цепочки атомов имеют пространственную периодичность с периодом а.

Разложим периодическую функцию Ф(x,y,z) в ряд Фурье в комплексной форме по пространственным гармоникам по оси x, полагая при этом, что по осям y и z предварительно произведено усреднение электронной плотности,   

 

Ф(x) = C_n exp (inkx),                                               (2.26)

 

где k =2p/ a - пространственная частота первой гармоники,            С_n - коэффициенты разложения или амплитуды Фурье-гармоник. Если функция Ф(x) нормирована на отрезке от - а /2 до а /2, то коэффициенты С_n  ряда (2.26) можно определить посредством интегрирования на этом отрезке

                a /2

С_n  = 1/ a  ò Ф(x)exp(-inkx)dx.                                                  (2.27)

             - a /2

Достаточным условием применимости разложения Фурье являются некоторые математические ограничения, сводящиеся к тому, что функция Ф(x) должна быть непрерывной или иметь конечное число разрывов, а также в пределах одного периода иметь конечное число максимумов и минимумов (условие Дирихле). Вполне естественно, что большинство функций распределения удовлетворяют этим условиям.

Можно предположить, что распределение электронной плотности в реальных периодических структурах имеет сравнительно гладкий характер, т.е. не имеет очень резких перепадов, как и большинство других распределений в статистической физике. В таком случае ряд Фурье (2.26) будет быстро спадать с увеличением n, т.е. не будет иметь в своем составе очень высокочастотных пространственных гармоник.

Хорошо известно, что слагаемые ряда Фурье являются взаимно ортогональными функциями при интегрировании их по оси x. Таким образом, ряд (2.26) можно рассматривать как разложение функции Ф(x) по собственным ортогональным функциям Ф_n(x), причем квадрат модуля коэффициента | С_n |² означает спектральный вклад n -й гармоники в общий частотный спектр.

Существенно отметить, что согласно (2.26) функция распределения электронов по координатам в периодической структуре имеет дискретный частотный спектр. Можно ожидать, что и функция распределения электронов по импульсам также будет дискретной.

Подставив значение функции Ф(х) из ряда Фурье (2.26) в выражение функции j(р_х) (2.19), мы можем вычислить ее явный вид

 

 

     (2.28)

 

Воспользовавшись свойствами дельта – функции d(х)

 

    d (k) = (1/2p) exp(ikx)dx                                                 (2.29)

 

и вычислив интеграл (2.28) по х, получаем

 

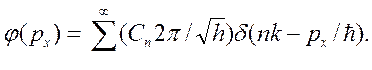                        (2.30)

 

    Мы действительно получили дискретный спектр функции j(р_х), причем импульсы электронов р_х могут принимать лишь значения

 

                       p_xn = nћk,  (n = 1,…,¥).                                          (2.31)

 

Отсюда можно заключить, что такая электронная система в периодической структуре может обмениваться лишь дискретными импульсами, кратными ћk, что и объясняет дифракцию любых частиц на монокристаллах, а также условия Вульфа – Брэгга (2.1)-(2.2).

                                              

Приложение 3

 

ОПТИКА

 

3.1. Связь энергии с частотой. Динамическое уравнение Шредингера

        

Рассмотрим систему, состоящую из большого числа атомов, т.е. вещество. Распределение электронной плотности в веществе при стационарном движении электронов описывается стационарной функцией распределения w(x,y,z), уравнение для которой мы вывели в прил. 2. Отметим, что под стационарным распределением следует понимать усредненную за бесконечное время наблюдения плотность электронной плазмы в веществе. Однако из-за статистического характера движения электронов электронная плотность не остается постоянной, а непрерывно флуктуирует во времени за счет естественного орбитального движения электронов в атомах и молекулах. Таким образом, для установления более полной динамической картины поведения электронной плазмы необходимо учитывать временную зависимость функции распределения. При этом функция распределения будет иметь вид: w(x,y,z,t). Требуется определить характер этой зависимости и, в частности, зависимость от времени комплексной амплитуды функции распределения Ф(x,y,z,t).

С этой целью воспользуемся законом сохранения полного заряда в веществе, который в дифференциальной форме известен как уравнение непрерывности для плотности заряда r и плотности электрического тока j = v r, где v - средняя скорость электронов,

   

¶r/¶t + div j = 0.                                                   (3.1) 

                     

Используя статистический метод описания, выразим плотность электрического заряда через функцию распределения электронной плотности w(x,y,z,t) и заряд электрона e

 

r(x,y,z,t) = ew(x,y,z,t) = e | Ф(x,y,z,t)| ².                                (3.2) 

        

Подставив это выражение в (3.1) и сократив заряд e, получим уравнение непрерывности для функции распределения электронной плотности 

            

¶ /¶ t | Ф |² + div | Ф |²  v = 0.                                  (3.3)  

      

Данное уравнение на языке статистической механики может быть интерпретировано следующим образом. Первый член уравнения означает изменение функции распределения во времени в данной точке пространства. Второй член имеет смысл потока функции распределения или потока плотности вероятности через малую сферу, окружающую данную точку, в соответствии с определением дивергенции вектора.     Вполне естественно, что от функции распределения некоторой  физической величины (заряда, массы, энергии и т.д.) можно всегда перейти к описанию поведения во времени самой физической величины в терминах механики сплошной среды [83].                                                                                                                                                                                                                                              Таким  образом, использование той или иной   функции распределения является мостиком или связующим звеном между описанием движения дискретных объектов в статистической механике и в механике непрерывных сред, которые всегда являются некоторой идеализацией реального вещества, состоящего из атомов и молекул. Недооценка этого подхода породила в квантовой теории представление об отдельной частице как о протяженном (размытом) в пространстве объекте: например, волна де Бройля, волновой пакет или электрон в виде облака, хотя речь идет, как правило, всего лишь о функции распределения плотности вероятности местонахождения частицы в заданном объеме.

С целью определения временной зависимости Ф(x,y,z,t) приведем уравнение (3.3) к виду

 

¶ /¶ t (Ф*Ф) = - div(Ф*Ф v ).                                  (3.4)  

 

    Преобразуем правую часть (3.4) к симметричной форме с заменой скорости v на импульс электрона p = m v

 

    ¶ /¶ t(ФФ*) = - (1/2m)div(Ф* р Ф + Ф р Ф*).                                (3.5)

 

    Теперь воспользуемся методом Фурье, примененным для вывода стационарного уравнения Шредингера (2.25), и произведем замену импульса р в (3.5) дифференциальным оператором в соответствии с выражением

 

              р Ф = - iћ ÑФ.                                                          (3.6)

 

Подставляя (3.6) в (3.5) и выполнив дифференцирование, получаем

    ¶ /¶ t(ФФ*) = (iћ/2m)(Ф* D Ф + Ф D Ф*).                           (3.7)

 

    Для приведения уравнения к удобному виду с целью совместного его решения со стационарным уравнением Шредингера (2.25) умножим все члены (3.7) на iћ, раскроем скобки в левой части, а в правую часть прибавим и вычтем слагаемое Ф*UФ. После соответствующей перегруппировки слагаемых в получившемся уравнении имеем

 

iћФ*¶ Ф/¶ t – [iћФ*¶ Ф/¶ t]* = - (ћ²/2m)Ф*DФ + Ф*UФ –

    [- (ћ²/2m)Ф*DФ + Ф*UФ]*.                                       (3.8)

 

Данное сложное уравнение состоит фактически из двух комплексно сопряженных частей более простого уравнения

    iћ ¶Ф/¶ t = - (ћ²/2m)DФ + UФ,                                   (3.9)

 

где произведено сокращение на Ф *.

    Мы получили динамическое уравнение Шредингера, которое было введено им также в виде постулата, исходя из волновых соображений в 1926 году. Если потенциальная энергия U(x,y,z) не зависит от времени, то в уравнении (3.9) можно произвести разделение переменных, записав функцию Ф в виде произведения временной и пространственной функций

     

Ф(x,y,z,t) = В(t)П(x,y,z).                                      (3.10)

 

Подставим это выражение в уравнение (3.9)

 

iћ П dB/dt = -(ћ²/2m) ВDП + U ВП                                (3.11)

 

и поделим обе части уравнения (3.11) на ВП

 

iћ 1/В dB/dt = - ћ²/2m (DП)/П + U.                              (3.12)

 

    Хорошо видно, что левая часть уравнения (3.12) зависит только от времени, а правая часть - только от координат. Для любых значений t и координат это возможно только в том случае, если обе части уравнения равны некоторой константе Е, называемой параметром разделения. В результате мы получаем два независимых уравнения

 

iћ dB/dt = E B                                                     (3.13)

и                     (- ћ²/2m) DП + U П = E П.                        (3.14)

 

Второе уравнение является стационарным уравнением Шредингера, которое было выведено нами ранее методом Фурье. Уравнение (3.13) легко решается и приводит к следующей временной зависимости функции В(t):

 

В(t) = exp(-iEt/ћ) = exp(-iw t),                                       (3.15)

 

где w = E/ћ - боровская частота. Данное уравнение могло быть получено и на основе гармонического Фурье-анализа из соотношения

 

              ¶ Ф/¶ t = iw Ф.                                                    (3.16)

 

Проанализируем различные возможные варианты решения уравнений (3.13) и (3.14). Если параметр разделения Е является комплексным, то функция В(t) будет изменяться во времени по модулю, что приведет к изменению электронной плотности в данной области пространства, т.е. соответствует нестационарному процессу, а полная энергия не является интегралом движения системы. При этом будет происходить либо поглощение, либо излучение электромагнитной энергии в зависимости от характеристик системы. В том же случае, если параметр разделения является действительной величиной, модуль функции В(t) становится постоянным и зависимость В(t) является гармонической с частотой колебаний w. Это соответствует стационарному движению электронов в атомах и молекулах, т.е. параметры движения в системе остаются постоянными.

 

3.2. Поглощение и излучение электромагнитной энергии атомами

 

Весь накопленный к настоящему времени богатый экспериментальный материал со всей определенностью показывает, что процессы поглощения и излучения электромагнитной энергии атомами было бы ошибочно считать как только элементарные акты поглощения и излучения некоторых гипотетических квантов энергии или фотонов. Это связано с тем обстоятельством, что способов подвода энергии к атомам, а также механизмов освобождения энергии из атомов существует большое множество. Вопросы, рассмотренные в данном разделе, можно отнести не только к атомам, но также и к молекулам или другим более сложным атомным системам.

Ранее нами были приведены основные необходимые условия существования стационарных орбит в планетарном атоме, т.е. те условия, при которых имеется запрет на излучение электромагнитных волн атомами, находящимися в основном состоянии. Теперь мы рассмотрим электромагнитные механизмы, с помощью которых атомы могут либо поглотить энергию, либо освободиться от избытка полной энергии над основным состоянием.

 

 

ПОГЛОЩЕНИЕ ЭНЕРГИИ

 

Начнем с механизмов, управляющих переходами атомов в возбужденные состояния. Одним из простейших способов передачи энергии атомам является обычное столкновение частиц. Два одинаковых атома, находящиеся в основном состоянии и имеющие некоторую ненулевую скорость сближения, при взаимном столкновении могут преобразовать кинетическую энергию атомов (в основном ядер) в потенциальную энергию возбуждения электронных оболочек. Такие столкновения атомов называются неупругими. При этом электроны переходят на орбиты, более удаленные от ядра, чем это было в основном состоянии. Вместе с потенциальной энергией увеличивается и полная энергия атомов. Таким способом, например, возбуждаются атомы кристаллической решетки твердого тела при тепловых колебаниях решетки или атомы газа, а также жидкости, нагретые до некоторой температуры Т.

Перевести атомы в возбужденное состояние можно посредством воздействия на них любыми быстрыми частицами, взаимодействующими с электронами оболочек. Подобные методы возбуждения атомов называются безызлучательными процессами, поскольку осуществляются через непосредственное взаимодействие кулоновских и магнитных полей сталкивающихся частиц.

Таким образом, мы видим, что способ подвода энергии к атому может быть практически произвольным и не имеет принципиального значения. Существенным является лишь преодоление некоторого энергетического порога возбуждения атома, ниже которого атом не способен перейти в возбужденное состояние в силу дискретного характера его энергетических уровней.

Особое место в данных процессах можно отвести возбуждению атомов посредством облучения их электромагнитными волнами, поскольку данное явление длительное время с классической точки зрения оставалось малоизученным и непонятым.

Хорошо известно, что в кристаллофосфорах свет может поглощаться одними активными центрами - центрами поглощения, а излучаться другими активными центрами - центрами свечения. Таким образом, в веществах существует перераспределение электромагнитной энергии между атомами. Миграция энергии в кристаллической решетке особенно активно происходит между однотипными центрами (явление концентрационного тушения). Исходя из этого, можно заключить, что поглощение света происходит резонансно одновременно очень многими

атомами вещества. Затем эта поглощенная энергия, перераспределяясь, мигрирует по веществу и концентрируется в отдельных атомах, в которых происходят переходы в возбужденные состояния с последующим излучением.

Таким путем снимается противоречие между непрерывным взаимодействием света со всеми электронами вещества и дискретными процессами, происходящими в отдельных избранных атомах, что внешне напоминает явление обмена энергией с гипотетическими частицами, именуемыми фотонами.

При отсутствии центров поглощения или диссипации энергии, тем не менее, взаимодействие света с веществом остается весьма существенным и проявляется в отражении, преломлении и рассеянии света.

Таким образом, электромагнитные волны воздействуют на каждый электрон вещества, однако результат воздействия будет заметным, если частота движения электронов в веществе будет близка к частоте падающего излучения. Такое взаимодействие происходит по обычным законам классической электродинамики и хорошо описывается теорией Максвелла- Лоренца [84-92].

Учитывая те обстоятельства, что способ возбуждения атомов не имеет принципиального значения, что процесс возбуждения атомов с помощью электромагнитных волн носит резонансный характер, а также зависит от ориентации электрического вектора волны Е по отношению к кристаллическим осям твердых тел, можно сделать предположение, что передача электромагнитной энергии электронам атомов в веществе происходит примерно так же, как это имеет место при акустическом возбуждении молекул или кристаллов.

 

ИЗЛУЧЕНИЕ ЭНЕРГИИ

 

В классической атомной физике излучение атома принято рассматривать на основе электрической дипольной модели [90]. Однако следует учесть, что дипольной моделью в теории Максвелла-Герца обычно пользуются для описания излучения макроскопических антенн, когда в процессе участвует огромное количество электронов.

Для анализа процесса излучения отдельного электрона в атоме более корректным является вычисление векторов Е и Н с использованием запаздывающих потенциалов Льенара-Вихерта. В этом случае можно избежать тех ошибок, которые обычно возникают при вычислении электромагнитных полей для электронов, движущихся по сложным траекториям.

Учитывая то обстоятельство, что существует множество различных способов высвобождения электромагнитной энергии, накопленной атомами, процесс излучения электромагнитных волн как отдельными атомами, так и большим количеством атомов (или веществом) было бы ошибочно считать элементарными актами в виде излучения гипотетических фотонов. Вспомним лишь некоторые из этих механизмов.

Можно привести массу примеров, когда электромагнитная энергия, поглощенная в условиях резонанса, т.е. при наличии явных переходов между уровнями энергии примесных атомов в веществе или центров окраски, затем безызлучательно преобразуется в тепловые колебания атомов вещества, т.е. в обычную механическую энергию. И лишь в хороших люминофорах, синтезированных из химически чистых веществ, при наличии подходящих каналов передачи энергии от поглощающих центров к излучающим, энергия возбуждения центров окраски может быть с высокой эффективностью преобразована в электромагнитное излучение.

Энергия от возбужденного атома к атому, находящемуся в основном состоянии, может быть передана безызлучательным путем, т.е. посредством обычных локальных электромагнитных полей в результате так называемых столкновений второго рода в газах [91], что широко используется в лазере, работающем на смеси углекислого газа, азота и гелия, а также в гелий-неоновом лазере. При этом процесс передачи энергии возбуждения от одного атома к другому может происходить как при наличии резонанса между уровнями энергии атомов, так и при отсутствии резонанса. Процессы нерезонансной передачи возбуждения при столкновении атомов используются также для создания инверсной заселенности в ряде лазеров непрерывного действия, работающих на переходах ионов металлов.

Довольно интересным является процесс передачи энергии безызлучательным путем от одного электрона к другому внутри одного и того же атома при оже-эффекте [92]. Этот процесс включает в себя заполнение одним из электронов оболочки атома вакансии, образованной на одном из внутренних уровней энергии атома, с безызлучательной передачей выделенной при этом энергии электрону другого (вышележащего) уровня и переводом его в возбужденное состояние. Если переданная энергия достаточна, то возбужденный электрон покидает атом (оже-электрон). Первичная вакансия может быть образована, например, при облучении атома рентгеновским излучением, электронами или ионами с достаточной энергией.

Из рассмотренных способов передачи энергии от возбужденных атомов к другим объектам можно сделать вывод, что излучение электромагнитной энергии в виде поперечных электромагнитных волн атомами возможно в тех случаях, когда данный процесс не будет подавлен (потушен) другими каналами утечки энергии возбуждения, которые очень часто бывают значительно более эффективными, как это происходит, например, в случае тушения люминесценции в кристаллах посторонними примесями.

Попытаемся проанализировать механизм излучения электромагнитных волн атомами, который бы не противоречил ни законам сохранения, ни принципу причинности, ни всем известным в настоящее время экспериментальным данным. Поскольку эксперименты проводятся, как правило, с веществами, а не с отдельными атомами, то в качестве примера рассмотрим систему, состоящую из множества атомов.

Допустим, что подавляющая часть атомов находится в основном состоянии с энергией Е_o  и некоторая часть атомов - в возбужденном состоянии с энергией Е₁. При этом среднестатистические частоты движения электронов равны w₀ = Е₀/ћ и w₁ = Е₁/ћ, соответственно.

Каждое из этих движений в отдельности является стационарным и может быть описано комплексными амплитудами функций распределения Ф₀ = R₀(x,y,z)exp(-iw₀ t) и Ф₁ = R₁(x,y,z)exp(-iw₁ t). Функции Ф₀  и Ф₁  являются собственными функциями уравнения Шредингера (3.14). В силу линейности уравнения Шредингера функция Ф = С₀Ф₀ + С₁Ф₁  , являющаяся суперпозицией двух различных амплитуд, также является решением данного уравнения. При этом коэффициенты С₀  и С₁  отражают парциальный вклад каждого состояния в общую систему атомов.

Вычислим общую функцию распределения рассматриваемой системы w = | Ф |²

 

w = | C₀Ф₀ + С₁Ф₁ |² = | C₀R₀(cos w₀ t - i sin w₀ t) + C₁R₁(cos w₁ t -

i sin w₁ t) |² = | C₀R₀ |² + | C₁R_1|²  + 2| C₀R₀C₁R₁ | cos (w₀ - w₁ )t.           (3.17)

                 

Мы видим, что данное выражение имеет интерференционный член, который описывает гармонические колебания с частотой биений между двумя боровскими частотами w₀    и w₁  .

Формула (3.17) показывает результат сложения двух гармоник в комплексной форме. Колебания электронной плотности означают колебания среднего электрического заряда с разностной частотой или частотой биений w₀  -  w₁. Следовательно, на разностной боровской частоте возможно дипольное излучение поперечных электромагнитных волн при выполнении всех законов сохранения. Другими словами, к электронной системе, совершающей колебания, должна быть подведена дополнительная энергия возбуждения, которую предстоит излучить, а также обеспечить обмен механическими моментами орбитальных электронов с соседними атомами. В противном случае излучение будет отсутствовать даже при наличии разностных частот движения электронов в одном и том же атоме.

Факт излучения электромагнитных волн атомами на разностных боровских частотах составляет так называемый комбинационный принцип Ритца, установленный им чисто эмпирически еще задолго до создания теории Бора [79].

Таким образом, мы установили, что разностная частота, на которой происходит излучение поперечных электромагнитных волн, непосредственно связана с реальными средними частотами статистического движения электронов в атомах в полном соответствии с законами электродинамики и классической физики.

Шредингер был одним из первых, кто разгадал этот механизм [1]: а именно, рассматривая атомы как систему колеблющихся электронов, он предложил связать условие частот Бора с появлением биений, так что боровская формула для частоты излучения n = E₁ / h - E₂ / h выражала просто тот факт, хорошо известный из акустики или волновой электромагнитной теории, что частота биений - гетеродинная частота - равна разности двух одновременных характеристических частот излучателя.

В результате рассмотренного механизма излучения система атомов, имеющая в своем составе различные возбужденные орбиты электронов с разными средними частотами движения, становится своеобразным электронным преобразователем энергии возбуждения атомов в частоту излучения поперечных электромагнитных волн. При этом, судя по спектроскопическим данным, можно отметить, что пропорциональная связь энергии с частотой выполняется с очень высокой точностью.

Проведенный детальный анализ механизма излучения электромагнитных волн атомами открывает тайну знаменитой квантовой формулы для фотонов: E = hn, подчеркивая то обстоятельство, что фотонов и так называемых квантов как элементарных частиц в природе не существует. А имеется самое обычное взаимодействие электронных оболочек атомов и молекул с электромагнитными полями в полном соответствии с законами классической электродинамики.

 

3.3. Cвязь объемной спектральной плотности энергии излучения абсолютно черного тела со средней энергией дипольного излучателя

 

В основу вычислений для нахождения необходимого соотношения положена электромагнитная теория резонансного рассеяния света атомами [74]. Предположим, что при отсутствии возбуждающего излучения электроны в атомах двигаются по стационарным орбитам с некоторой средней частотой w₀, не излучая электромагнитных волн в силу запрета на излучение законом сохранения орбитального механического момента электронов.

Электрическое поле падающей световой волны E = E₀ exp(iwt) раскачивает электроны от равновесной орбиты, и они, двигаясь с ускорением, начинают излучать. В данном случае гармонические колебания электронов под действием возмущающего электрического поля происходят по одной прямой в направлении, совпадающем с направлением электрического вектора Е, поэтому запрета на излучение по механическому моменту не существует. Когда частота падающей волны w совпадает с частотой движения электрона на орбите w₀  , наступает резонанс и поглощение волн становится максимальным.

Допустим, что возмущающее электрическое поле направлено вдоль оси x. Тогда уравнение движения электрона под действием световой волны имеет вид

 

x + g x + w₀² x = F/m,                     (3.18)

 

где g - постоянная затухания колебаний, F = eE - вынуждающая сила, m - масса электрона. Уравнение (3.18) обычно решается в комплексном виде, в результате чего находится комплексная амплитуда отклика осциллятора X на силу F

 

X = F/m(w₀² - w² + i g w).                        (3.19)

 

Опуская часть выкладок теории дипольного излучения, изложенной в работах [73,74], приведем лишь основные результаты вычислений. Полная мощность, излучаемая диполем во всех направлениях, равна

 

P = e²w⁴x₀²/12p e₀  c³,                               (3.20)

 

где x₀  - амплитуда колебаний электрона.

С учетом выражения (3.19) из (3.20) получается [73]

 

P =(e₀ cE₀²/2)(8p r₀²/3)w⁴/[(w² -w₀²)² + g²w²],               (3.21)

 

где E₀  - амплитуда электрического вектора световой волны ,                r₀  = e²/4p e₀ mc²  - классический радиус электрона. Величина e₀ cE₀²/2 = I означает интенсивность падающего света. В этом случае выражение (3.21) записывается в простой форме

 

P = I s,                                      (3.22)

 

где s - эффективное сечение рассеяния света во всех направлениях

 

s = (8p r₀²/3)w⁴/[(w² - w₀²)² + g²w²].                                     (3.23)

 

При высокой добротности Q осциллятора (в случае электрона Q - порядка 10⁸) s как функция частоты имеет заметную величину только для w  вблизи собственной частоты w₀. В этом диапазоне частот выражение (3.23) приобретает вид

 

s = (2p r₀²w₀²/3)/[(w  -  w₀)² + g²/4].                                    (3.24)

 

Для нахождения полной рассеянной мощности света необходимо вычислить интеграл по всем w

                           ¥

P = ò I(w)s(w)dw.                                              (3.25)

                           0

При этом можно предположить, что неизвестное спектральное распределение света I(w) - это плавная кривая, которая в узкой области частот вблизи w₀, где s имеет острый максимум, меняется не очень сильно, и поэтому I(w) при интегрировании можно считать константой. С учетом резонансного характера кривой пределы интегрирования можно сделать от -¥ до ¥. Таким образом, интеграл сводится к табличному и легко вычисляется. В результате вычислений получаем для рассеянной мощности

 

P = 4p²r₀²w₀²I(w₀)/3g.                               (3.26)

 

Теперь обратимся к уравнению для средней энергии осциллятора W, выражающему экспоненциальное уменьшение энергии колебаний во времени,

-P = dW/dt = -gW.                                     (3.27)

 

Уравнение (3.27) записано для одномерного случая. При колебаниях электрона вдоль трех осей x,y,z правую часть (3.27) нужно умножить на 3, тогда

 

                                 P = 3gW.                                           (3.28)

 

Из (3.26) и (3.28) получаем

 

I(w₀) = 9g²W/4p²r₀²w₀².                               (3.29)

 

Для осциллятора средняя энергия колебаний равна удвоенной средней кинетической энергии или максимальной кинетической энергии K_max

 

W = 2<K> = m v _max²/2 = mw₀²x₀²/2.                     (3.30)

 

Из (3.20), (3.27) и (3.30) находим

 

g= e²w²/6pe₀mc³ = 2r₀w²/3c.                      (3.31)

 

Подставив значение g в (3.29), имеем

 

I(w) = w²W/p²c².                               (3.32)

 

    Принимая во внимание соотношение между интенсивностью света I и плотностью энергии r

I = rc,                                    (3.33)

 

от формулы для интенсивности света (3.32) переходим к выражению для плотности энергии излучения

r(w)   =   w²W/p²c³.                 (3.34)

 

Таким образом, нам удалось связать спектральную плотность энергии излучения со средней энергией колеблющегося электрона W, находящегося в полости абсолютно черного тела. Далее предстоит связать среднюю энергию W с температурой стенок Т излучателя.

3.4. Спектр излучения абсолютно черного тела. Формула Планка

 

Естественно предположить, что падающее на стенки излучающего тела электромагнитное излучение приведет к нагреву стенки и заставит атомы колебаться. Атомы кристаллической решетки, сталкиваясь между собой в процессе колебаний, будут переводить энергию колебаний во внутреннюю энергию возбуждения электронных оболочек e с последующим излучением данной энергии в виде электромагнитных волн обратно в полость. В процессе обмена энергией между излучением и возбужденными атомами в конечном итоге должно установиться равновесие, т.е. количество поглощенной атомами энергии будет равняться количеству излученной ими электромагнитной энергии.

Процесс возбуждения атомов обычно происходит согласно статистическим закономерностям, поэтому для дальнейшего анализа воспользуемся законами статистической физики и термодинамики.

 

ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ. ЗАКОН СМЕЩЕНИЯ ВИНА

 

    Важные результаты в термодинамике излучения были получены В. Вином (1864-1928) в 1893-1894 гг. Вин доказал, что равновесное излучение, заключенное в оболочке с идеально отражающими стенками, будет оставаться равновесным при квазистатическом сжатии или расширении оболочки. Кроме этого, им частично была решена задача по определению спектрального состава равновесного излучения (закон Вина) [93,94].

    Поскольку формула Вина для спектральной плотности излучения представляет большой интерес и будет далее нами использована, приведем ее вывод, изложенный в работе [94].

    Вначале получим уравнение адиабаты. Для этого представим, что равновесное излучение заполняет оболочку сферической формы с объемом V. При этом можно считать, что излучение является изотропным. Из волновой теории с учетом трех степеней свободы следует, что для изотропных волн плотность энергии волн r и давление волн на стенки p связаны соотношением

                                 p = r/ 3.                                                (3.35)

 

Полная энергия излучения в оболочке равна rV. При увеличении объема оболочки на dV за счет энергии волн совершается работа pdV, поэтому увеличение полной энергии равно

 

    pdV = - d(rV) = - Vdr -rdV.                                             (3.36)

 

С учетом (3.35) этому уравнению можно придать вид

 

              4 rdV + 3 Vdr = 0.                                                             (3.37)