Способ соединения фаз источника и фаз приемника, показанный на рис. 6.2 и 6.5, называется соединением звездой. Общая точка трех фаз (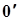 у источника,
у источника,  у приемника) называется нейтралью или нулем. Источник и приемник могут быть соединены либо четырехпроводной линией (рис. 6.2), либо трехпроводной линией (рис. 6.5). Провод, соединяющий нейтрали источника и приемника, называется нулевым проводом. Провода, соединяющие зажимы источника (
у приемника) называется нейтралью или нулем. Источник и приемник могут быть соединены либо четырехпроводной линией (рис. 6.2), либо трехпроводной линией (рис. 6.5). Провод, соединяющий нейтрали источника и приемника, называется нулевым проводом. Провода, соединяющие зажимы источника ( ) с зажимами приемника (
) с зажимами приемника ( ), называются линейными проводами.
), называются линейными проводами.

Рис. 6.5. Трехфазная цепь звезда – звезда
Напряжения на фазах источника (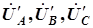 ) и фазах приемника (
) и фазах приемника (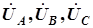 ) называются фазными напряжениями. Напряжения между проводами линии, соединяющей источник и приемник, (
) называются фазными напряжениями. Напряжения между проводами линии, соединяющей источник и приемник, ( ) называются линейными напряжениями. В каждой фазе источника и приемника и соединяющем их проводе линии протекает одинаковый ток (например, ток
) называются линейными напряжениями. В каждой фазе источника и приемника и соединяющем их проводе линии протекает одинаковый ток (например, ток  на рис. 6.5), этот ток является одновременно и фазным, и линейным. При наличии нулевого провода (рис. 6.2) напряжения между любым линейным и нулевым проводом равно соответствующему фазному напряжению.
на рис. 6.5), этот ток является одновременно и фазным, и линейным. При наличии нулевого провода (рис. 6.2) напряжения между любым линейным и нулевым проводом равно соответствующему фазному напряжению.
На рис. 6.6 показана векторная диаграмма линейных и фазных напряжений. Построение диаграммы начато с симметричной трехлучевой звезды векторов ЭДС  и
и  . Напряжения на фазах источника равны ЭДС соответствующих фаз (
. Напряжения на фазах источника равны ЭДС соответствующих фаз ( и т. д.). Линейные напряжения определяются по второму закону Кирхгофа:
и т. д.). Линейные напряжения определяются по второму закону Кирхгофа:
 ,
,  ,
, 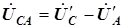 . (6.2)
. (6.2)
Вектор  направлен из конца вектора
направлен из конца вектора  в конец вектора
в конец вектора  . Аналогично построены векторы
. Аналогично построены векторы 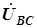 и
и  . Линейные напряжения одинаковы по величине и отличаются фазами на
. Линейные напряжения одинаковы по величине и отличаются фазами на  .
.
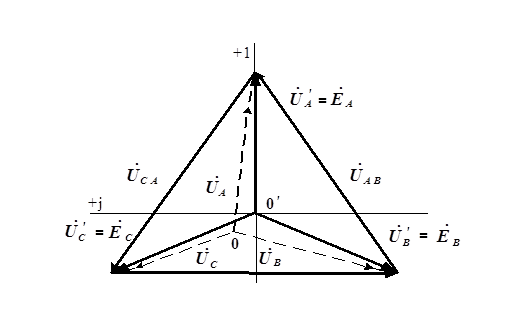
Рис. 6.6. Векторная диаграмма напряжений для трехфазной цепи звезда – звезда
Фазные напряжения приемника связаны с линейными напряжениями уравнениями, аналогичными уравнениям (6.2),
 ,
,  ,
,  . (6.3)
. (6.3)
Векторы  ,
,  и
и  нанесены на рис. 6.6 штриховыми линиями. В общем случае напряжения на фазах приемника различны по величине, и, как видно из диаграммы, точки
нанесены на рис. 6.6 штриховыми линиями. В общем случае напряжения на фазах приемника различны по величине, и, как видно из диаграммы, точки 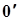 и
и  , соответствующие нейтралям источника и приемника, не совпадают. Между нейтралями источника и приемника появляется напряжение, которое называют напряжением смещения нейтрали.
, соответствующие нейтралям источника и приемника, не совпадают. Между нейтралями источника и приемника появляется напряжение, которое называют напряжением смещения нейтрали.
Все фазные напряжения источника одинаковы по величине
 ,
,
и все линейные напряжения равны между собой
 .
.
Соотношение между величинами линейных и фазных напряжений можно определить с помощью векторной диаграммы (рис. 6.6). Например,
 .
.
Этот расчет можно проверить по формулам (6.1) и (6.3).
| И 6.2 | При соединении фаз звездой линейное напряжение в  раз больше фазного напряжения, раз больше фазного напряжения,
 . .
|
Если линейное напряжение равно 380 В, то фазное напряжение близко к 220 В; если линейное напряжение равно 220 В, то фазное напряжение несущественно отличается от 127 В.
 2020-04-07
2020-04-07 237
237








