Занятие 4 Угол между двумя векторами. Проекция вектора на ось 25.03
4.1 Составить таблицу №9 по той же схеме. Практическая.работа
http://fxdx.ru/page/ugol-mezhdu-vektorami-ugol-mezhdu-vektorom-i-osju-proekcija-vektora-na-os
4.2. теоретический материал на указанном сайте, составить таблицы по той же схеме.
umath.ru
изучаем математику вместе
Уравнения прямой
Таблица №7
Уравнения прямой на плоскости в координатной форме
1) общее уравение прямой
2) параметрическое уравнение прямой
3) параметрическое уравнеие прямой в кононической форме
4) уравнение прямой, проодящей через 2 точки
5) уравнение прямой в отрезках
Таблица № 8
Уравнения прямой на плоскости в векторной форме
1) векторное уравнение прямой в параметрической форме
2) нормальное уравнение прямой
3) векторное уравнение прямой, проодящей через 2 точки
Уравнения прямой в пространстве
Таблица №9
Уравнения прямой в пространстве в координатной форме
1) параметрическое уравнение прямой
2) параметрическое уравнение прямой в кононической форме
3) уравнение прямой, проходящей через 2 точки
4) прямая, как пересечение двух плоскостей.
Таблица №10
Уравнения прямой в пространстве в векторой форме.
1) векторное уравнение прямой в параметрической форме
2) векторное уравнение прямой
3) векторное уравнение прямой, проодящей через 2 точки
Занятие 5. Использование координат и векторов при решении математических задач 24.03
Разобрать задачи, записав их
Дано Чертёж
Найти Решение
Цель занятия: Научиться пользоваться формулами для решения простейших задач, освоить различные виды задач.
5.1 Использование координат и векторов
Задача1. В прямоугольной системе координат Oxyz точка М имеет координаты 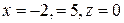 . Найти координаты ее радиус-вектора
. Найти координаты ее радиус-вектора 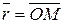 .
.
Решение. Абсцисса 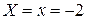 , ордината
, ордината 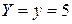 , аппликата
, аппликата 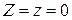 . Следовательно,
. Следовательно, 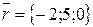 . Радиус-вектор
. Радиус-вектор 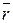 лежит в плоскости xОу.
лежит в плоскости xОу.
Задача 2. Найти координаты X, Y, Z суммы векторов 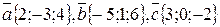 .
.
Решение. 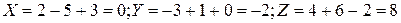 .
.
Следовательно, сумма векторов 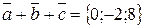 . Искомый вектор параллелен плоскости yOz так как его компонента по оси Оx равна нулю.
. Искомый вектор параллелен плоскости yOz так как его компонента по оси Оx равна нулю.
Задача 3. Найти сумму векторов 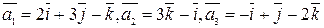 .
.
Решение. 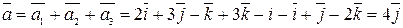 . Результат запишем так:
. Результат запишем так: 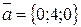 . Вектор
. Вектор 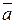 коллинеарен с осью оу.
коллинеарен с осью оу.
Задача 4. Найти координаты вектора 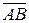 , если
, если 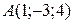 и
и 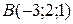 .
.
Решение. 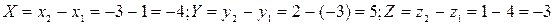 . Следовательно,
. Следовательно, 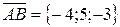 .
.
Задача 5. Найти длину вектора 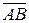 , если
, если 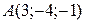 и
и 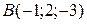 .
.
Решение. Воспользовавшись формулой 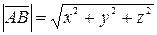 , получим
, получим 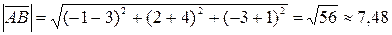 .
.
Задача 6. Найти скалярное произведение векторов 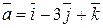 ,
, 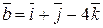 .
.
Решение. Скалярное произведение векторов найдем по формуле: 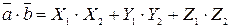 . Получаем
. Получаем 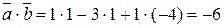 .
.
Задача 7. Найти угол между векторами 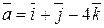 и
и 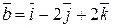 .
.
Решение. Воспользуемся формулой:
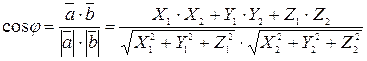 .
.
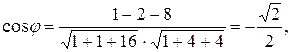
отсюда 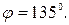
5.2 Решение задач по теме уравнение прямой
Цель занятия: Научиться пользоваться формулами для решения простейших задач, освоить различные виды уравнений прямой.
1. Расстояние между двумя точками. Деление отрезка в данном отношении.
2. Различные виды уравнений прямой.
3. Угол между двумя прямыми.
4. Расстояние от точки до прямой.
Задача 1. В прямоугольной системе координат Oxyz точка М имеет координаты 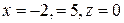 . Найти координаты ее радиус-вектора
. Найти координаты ее радиус-вектора 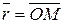 .
.
Решение. Абсцисса 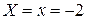 , ордината
, ордината 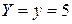 , аппликата
, аппликата 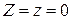 . Следовательно,
. Следовательно, 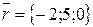 . Радиус-вектор
. Радиус-вектор 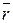 лежит в плоскости xОу.
лежит в плоскости xОу.
Задача 2. Найти координаты X, Y, Z суммы векторов 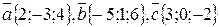 .
.
Решение. 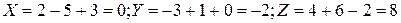 .
.
Следовательно, сумма векторов 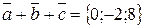 . Искомый вектор параллелен плоскости yOz так как его компонента по оси Оx равна нулю.
. Искомый вектор параллелен плоскости yOz так как его компонента по оси Оx равна нулю.
Задача 3. Найти сумму векторов 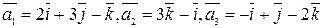 .
.
Решение. 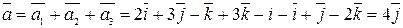 . Результат запишем так:
. Результат запишем так: 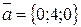 . Вектор
. Вектор 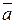 коллинеарен с осью оу.
коллинеарен с осью оу.
Задача 4. Найти координаты вектора 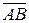 , если
, если 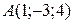 и
и 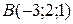 .
.
Решение. 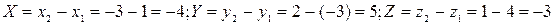 . Следовательно,
. Следовательно, 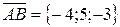 .
.
Задача 5. Найти длину вектора 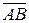 , если
, если 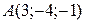 и
и 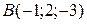 .
.
Решение. Воспользовавшись формулой 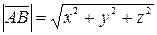 , получим
, получим 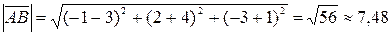 .
.
Задача 6. Найти скалярное произведение векторов 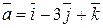 ,
, 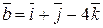 .
.
Решение. Скалярное произведение векторов найдем по формуле: 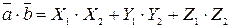 . Получаем
. Получаем 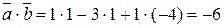 .
.
Задача 7. Найти угол между векторами 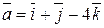 и
и 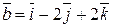 .
.
Решение. Воспользуемся формулой:
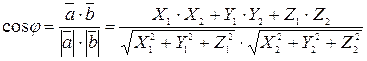 .
.
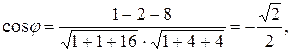
отсюда 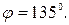
Занятие 6 Решение задач
6.1 Использование координат и векторов
1. Написать выражения компонент вектора 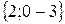 по осям координат.
по осям координат.
2. Написать разложение вектора 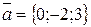 по координатным ортам.
по координатным ортам.
3. Даны векторы 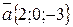 и
и 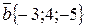 . Найти векторы
. Найти векторы 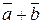 ,
, 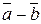 ,
, 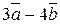 .
.
4. Записать в векторной форме отрезок, соединяющий две точки 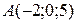 и
и 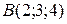 .
.
5. Длины векторов 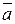 и
и 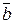 равны
равны 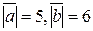 и угол между векторами
и угол между векторами
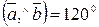 . Найти скалярное произведение векторов.
. Найти скалярное произведение векторов.
6. Найти длины векторов 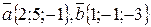 и скалярное произведение этих векторов.
и скалярное произведение этих векторов.
7. Найти угол между векторами 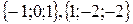 .
.
6.2 Использование уравнения прямой
1. Написать выражения компонент вектора 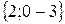 по осям координат.
по осям координат.
2. Написать разложение вектора 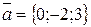 по координатным ортам.
по координатным ортам.
3. Даны векторы 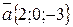 и
и 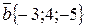 . Найти векторы
. Найти векторы 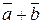 ,
, 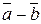 ,
, 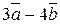 .
.
4. Записать в векторной форме отрезок, соединяющий две точки 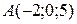 и
и 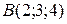 .
.
5. Длины векторов 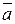 и
и 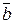 равны
равны 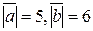 и угол между векторами
и угол между векторами
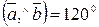 . Найти скалярное произведение векторов.
. Найти скалярное произведение векторов.
6. Найти длины векторов 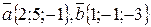 и скалярное произведение этих векторов.
и скалярное произведение этих векторов.
7. Найти угол между векторами 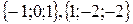 .
.
 2020-04-20
2020-04-20 146
146






