16.2.1. Алгоритм Робертса ─ Флореса
Рассмотрим алгоритм Робертса и Флореса для построения гамильтонова цикла на графе. Алгоритм основан на переборе вершин, входящих в анализируемые цепи. Рассматриваемая цепь непрерывно продлевается до момента, когда построен гамильтонов цикл или если эта цепь не приводит к его построению. Тогда рассматривается другая цепь, и процесс продолжается сначала, пока не будет найден гамильтонов цикл или будут рассмотрены все цепи и окажется, что этот цикл не найден.
Исходной информацией является специальная матрица M = | mij | k × n. Здесь k ─ это параметр, определяющий число строк матрицы. Величина mij определяет метку первой вершины, для которой есть ребро ui,j. Число строк матрицы равно наибольшей локальной степени в анализируемом графе. Например, задан граф G (рис. 16.19) и его матрица.
| a | b | c | d | e | f | |||
| 1 | b | a | a | c | b | a | ||
| М = | 2 | c | c | b | e | c | b | |
| 3 | f | e | d | – | d | c | . | |
| 4 | – | f | e | – | – | |||
| 5 | – | – | f | – | – |
.

Рис. 16.19. Граф G
Рассмотрим работу алгоритма на примере. Алгоритм начинается с рассмотрения элементов первого столбца матрицы М, если не задана иная начальная вершина гамильтонова цикла.
1.1. Выбираем вершину a. В списке вершин графа G, смежных с вершиной a (столбец a матрицы М), первой стоит вершина b.
1.2. Заносим в последовательность обхода вершин вершину b:
ГЦ = [ a ─ b ], переходим к столбцу b матрицы M.
1.3. Так как гамильтонов цикл еще не построен, продолжаем вычисления.
2.1. В списке вершин графа G, смежных с вершиной b, первой стоит вершина a, однако она уже задействована в цикле. Поэтому выбираем следующую вершину в столбце. Это вершина c.
2.2. Заносим в последовательность обхода вершин вершину c:
ГЦ = [ a ─ b ─ c ], переходим к столбцу c матрицы M.
2.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
3.1. В списке вершин графа G, смежных с вершиной c, вершины a и b мы пропускаем, так как они использованы в цикле. Выбираем вершину d.
3.2. Заносим в последовательность обхода вершин вершину d:
ГЦ = [ a ─ b ─ c ─ d ], переходим к столбцу d матрицы M.
3.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
4.1. В списке вершин графа G, смежных с вершиной d, пропускаем вершину c и выбираем вершину e.
4.2. Заносим в последовательность обхода вершин вершину e:
ГЦ = [ a ─ b ─ c ─ d ─ e ], переходим к столбцу e матрицы M.
4.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
5.1. В списке вершин графа G, смежных с вершиной e, все вершины уже задействованы в цикле.
5.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b - c ─ d ].
6.1. В списке вершин графа G, смежных с вершиной d, все вершины уже задействованы в цикле.
6.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ c ].
7.1. В списке вершин графа G, смежных с вершиной c, пропускаем вершину d и выбираем вершину e.
7.2. Заносим в последовательность обхода вершин вершину e:
ГЦ = [ a ─ b ─ c ─ e ], переходим к столбцу e матрицы M.
7.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
8.1. В списке вершин графа G, смежных с вершиной e, пропускаем вершины b и c, после чего выбираем вершину d.
8.2. Заносим в последовательность обхода вершин вершину d:
ГЦ = [ a ─ b ─ c ─ e ─ d ], переходим к столбцу d матрицы M.
8.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
9.1. В списке вершин графа G, смежных с вершиной d, все вершины уже задействованы в цикле.
9.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ c ─ e ].
10.1. В списке вершин графа G, смежных с вершиной e, все вершины уже задействованы в цикле.
10.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ c ].
11.1. В списке вершин графа G, смежных с вершиной c, пропускаем вершину e и выбираем вершину f.
11.2. Заносим в последовательность обхода вершин вершину f:
ГЦ = [ a ─ b ─ c ─ f ], переходим к столбцу f матрицы M.
11.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
12.1. В списке вершин графа G, смежных с вершиной f, все вершины уже задействованы в цикле.
12.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a - b - c ].
13.1. В списке вершин графа G, смежных с вершиной c, все вершины уже задействованы в цикле.
13.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a - b ].
14.1. В списке вершин графа G, смежных с вершиной b, пропускаем вершину c и выбираем вершину e.
14.2. Заносим в последовательность обхода вершин вершину e:
ГЦ = [ a ─ b ─ e ], переходим к столбцу c матрицы M.
14.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
15.1. В списке вершин графа G, смежных с вершиной e, пропускаем вершину b и выбираем вершину c.
15.2. Заносим в последовательность обхода вершин вершину c:
ГЦ = [ a ─ b ─ e ─ c ], переходим к столбцу c матрицы M.
15.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
16.1. В списке вершин графа G, смежных с вершиной c, выбираем вершину d.
16.2. Заносим в последовательность обхода вершин вершину d:
ГЦ = [ a ─ b ─ e ─ c ─ d ], переходим к столбцу d матрицы M.
16.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
17.1. В списке вершин графа G, смежных с вершиной d, все вершины уже задействованы в цикле.
17.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ e ─ c ].
18.1. В списке вершин графа G, смежных с вершиной c, выбираем вершину f.
18.2. Заносим в последовательность обхода вершин вершину f:
ГЦ = [ a ─ b ─ e ─ c ─ f ], переходим к столбцу f матрицы M.
18.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
19.1. В списке вершин графа G, смежных с вершиной f, все вершины уже задействованы в цикле.
19.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ e ─ c ].
20.1. В списке вершин графа G, смежных с вершиной c, все вершины уже задействованы в цикле.
20.2. Возвращаемся на шаг назад и пытаемся найти другой вариант продолжения обхода вершин графа: ГЦ = [ a ─ b ─ e ].
21.1. В списке вершин графа G, смежных с вершиной e, пропускаем вершину c и выбираем вершину d.
21.2. Заносим в последовательность обхода вершин вершину d:
ГЦ = [ a ─ b ─ e ─ d ], переходим к столбцу c матрицы M.
21.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
22.1. В списке вершин графа G, смежных с вершиной d, выбираем вершину c.
22.2. Заносим в последовательность обхода вершин вершину c:
ГЦ = [ a ─ b ─ e ─ d ─ c ], переходим к столбцу c матрицы M.
22.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
23.1. В списке вершин графа G, смежных с вершиной c, выбираем вершину f.
23.2. Заносим в последовательность обхода вершин вершину f:
ГЦ = [ a ─ b ─ e ─ d ─ c ─ f ], переходим к столбцу c матрицы M.
23.3. Гамильтонов цикл еще не построен, продолжаем вычисления.
24.1. В списке вершин графа G, смежных с вершиной f, выбираем вершину a, поскольку это завершающее ребро гамильтонова цикла.
23.2. Заносим в последовательность обхода вершин вершину a:
ГЦ = [ a ─ b ─ e ─ d ─ c ─ f ─ a ].
23.3. Гамильтонов цикл построен, работа алгоритма завершена.
Главное преимущество алгоритма ─ простота, а его основным недостатком является сложность в случае необходимости перебора всех путей в процессе построения гамильтонова цикла. В случае же, когда гамильтонова цикла в графе не существует, алгоритм и вовсе сведется к полному перебору всех возможных вариантов построения пути.
Если в графе можно построить несколько гамильтоновых циклов, то алгоритм позволяет последовательно определить все гамильтоновы циклы. Кроме того, алгоритм позволяет определять и гамильтоновы цепи.
Алгебраический метод
Идея алгоритма состоит в построении всех простых цепей в графе путем последовательного перемножения матриц графа. В качестве исходных матриц для перемножения используются модифицированная матрица смежности графа B и матрица перемножений PL. Модифицированная матрица смежности B = || bij ||, представляет собой матрицу, в которой если xi и xj смежны, то в ячейку матрицы вместо единицы заносится xj. На первом этапе матрица перемножений PL = || pL ( i , j )|| идентична матрице B, а элемент матрицы pL ( i , j ) представляет собой сумму внутренних произведений все простых цепей длиной l. Выражение вида x 2 ´ x 3 ´¼ ´ xk -1, получаемое в ячейке на пересечении строки x 1 и столбца xk, представляет собой цепь x 1, x 2, x 3, ¼, xk -1, xk.
Алгебраическое произведение матриц P’L+1 = B ´ PL представляет собой матрицу P’L+1 = úç p L+1( s , t )úç, где элемент p L+1( s , t ) = 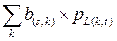 .
.
Из полученной таким образом матрицы алгебраического произведения P’L+1 исключаются элементы, расположенные на главной диагонали. Кроме того, из ячеек, содержащих суммы внутренних произведений, исключаются слагаемые, содержащие начальный элемент простой цепи в качестве сомножителя. Полученная после подобного преобразования матрица, обозначается нами как PL+1, после чего процесс повторяется. По достижении n ─ 1 шага все непустые элементы матрицы Pn-1 представляют собой гамильтоновы цепи, которые при наличии ребра u(xk ─ x 1) образуют гамильтоновы циклы.
 2020-04-07
2020-04-07 825
825








