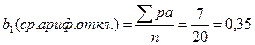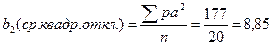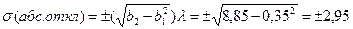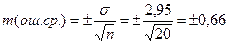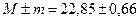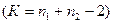2020-04-11
201
| Размерный ряд | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | n | ||||
|
| ||||||||||||||||||
| p | 1 0 1 2 1 3 1 3 1 3 1 2 | 20 | ||||||||||||||||
| 23,1 | a | -6 -5 -4 -3 -2 -1 +1 +2 +3 +4 +5 | ||||||||||||||||
| 22,2 | pa | -6 0 -4 -6 -2 -3 3 2 9 4 10 | ||||||||||||||||
| 21,1 | a2 | 36 25 16 9 4 1 1 4 9 16 25 | ||||||||||||||||
| 23,5 | pa2 | 36 0 16 18 4 3 3 4 27 16 50 | ||||||||||||||||
| 20,5 | А – усл. ср.= 22,5 | |||||||||||||||||
| 26,3 | Мср.=А+b1 = 22,5+0,35=22,85 | |||||||||||||||||
| 21,0 | ||||||||||||||||||
| 27,1 |
| |||||||||||||||||
| 21,5 | ||||||||||||||||||
| 25,6 | ||||||||||||||||||
| 23,4 |
| |||||||||||||||||
| 25,0 | ||||||||||||||||||
| 16,8 | ||||||||||||||||||
| 25,2 |
| |||||||||||||||||
| 19,3 | ||||||||||||||||||
| 24,7 | ||||||||||||||||||
| 19,6 |
| |||||||||||||||||
| 25,4 | ||||||||||||||||||
| 18,6 | ||||||||||||||||||
| 27,2 |
| |||||||||||||||||
После извлечения корня квадратного получаются значения со знаком плюс или минус; обычно берут только положительное значение.
Оценка достоверности собранного материала
Проблема достоверности занимает видное место в статистической теории.
Напомним, что генеральная совокупность – это вся подлежащая изучению совокупность данных объектов. В пределе она рассматривается как состоящая из бесконечно большого количества отдельных единиц. Та часть совокупности, которая подвергается исследованию, называется выборочной совокупностью или просто выборкой. Оба типа совокупностей характеризуются одинаковыми закономерностями и для их характеристики могут быть вычислены статистические показатели: средняя арифметическая и средне квадратическое отклонение.
Оказывается, что отдельные значения среднеарифметических выборок варьируют вокруг среднеарифметической генеральной совокупности М (мю). Вариация же выборочных средних вокруг М (мю) может быть измерена своим средним квадратическим отклонением, своей сигмой. Эта сигма получила название средней ошибки или среднеквадратической ошибки. Именно она указывает на степень близости М и m.
Средняя ошибка для М может быть вычислена по формуле 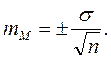7:
(7)
Она является ни чем иным, как среднеквадратическим отклонением вариационного ряда, составленного из отдельных значений М.
|
|
|
Для изучения закономерностей вариации при нормальном распределении широко пользуются так называемым нормированным отклонением, которое обозначается буквой t, и представляет собой отклонение той или другой варианты от средней арифметической, выраженное в сигмах:
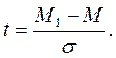(8)
Размещение вариант в вариационном ряду при нормальном распределении характеризуется определенными закономерностями.
Дело в том, что в нормальной кривой отклонения от средней арифметической укладываются в 6 сигм: 3 сигмы вправо и 3 сигмы влево от средней.
Для установления разницы между средними арифметическими двух рядов надо воспользоваться нормированным отклонением t, которое примет следующую формулу 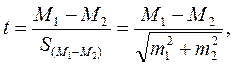9:
(9)
где числителем является разница между средними арифметическими двух групп (знак разницы не имеет значения), ее сокращенно обозначают буквой d. В знаменателе же средняя ошибка этой разницы, т.е.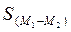 
, или более сокращенно Sd. Тогда:
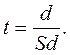(10)
Вероятность достоверности находится либо по таблицам нормального интеграла вероятности, при отсутствии таблиц можно исходить из правила 3-х сигм: если разница превышает свою ошибку почти в 3 раза, она достоверна с вероятностью не менее 0,99. Но в таком высоком значении t нет надобности. Если n >30, то t =2,58 гарантирует достоверность разницы с вероятностью 0,99, или ошибка не больше 3-х сигм.
Достоверность выборочной разницы измеряется особым показателем, который можно назвать критерием достоверности разницы.
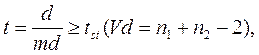(11)
где d = M 1- M 2 – разность выборочных средних;
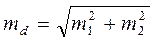– ошибка выборочной разности;
tst – стандартное значение критерия, определяемое по таблицам критериев Стьюдента (табл. 19), для заданного порога вероятности безошибочных прогнозов (0,95; 0,99; 0,999), в зависимости от числа степеней свободы n 1, n 2 – численности сравниваемых выборок
Vd = n 1 + n 2 – 2 – число степеней свободы для разности двух средних.
При использовании критерия достоверности разности возможны два случая:
1) td ≥ tst – полученный в исследовании критерий достоверности равен или превышает стандартное значение критерия, найденное по Стьюденту. В этом случае разность достоверна с определенной надежностью, т.е. соответствует по знаку генеральной разности. Если эмпирический критерий равен или превышает первый порог, он подчеркивается одной чертой, если равен или превышает второй и третий пороги, он подчеркивается двумя или тремя чертами.
2) td < tst – полученный критерий достоверности меньше стандартного значения для минимального или требуемого порога вероятности. В этом случае разность не достоверна, что значит:
а) по выборочной разности нельзя сделать никакой оценки генеральной разности;
б) осталось невыясненным, какая из двух средних больше;
в) осталось недоказанным как наличие, так и отсутствие различия между генеральными средними.
За минимальный порог достоверности в подавляющем большинстве принимается первый порог, соответствующий вероятности безошибочных прогнозов β1 – 0,95. Эмпирический критерий при недостаточной разнице подчеркивается волнистой чертой.
Таблица 19
Критические значения t критерия Стьюдента для трех уровней значимости (а)
и чисел степеней свободы (K)
| Числа степеней свободы | Уровни значимости, % | Числа степеней свободы | Уровни значимости, % | ||||
| 5 | 1 | 0,1 | 5 | 1 | 0,1 | ||
| 1 | 12,71 | 63,66 | - | 18 | 2,10 | 2,88 | 3,92 |
| 2 | 4,30 | 9,92 | 31,60 | 19 | 2,09 | 2,86 | 3,88 |
| 3 | 3,18 | 5,84 | 12,92 | 20 | 2,09 | 2,85 | 3,85 |
| 4 | 2,78 | 4,60 | 8,61 | 21 | 2,08 | 2,83 | 3,82 |
| 5 | 2,57 | 4,03 | 6,87 | 22 | 2,07 | 2,82 | 3,79 |
| 6 | 2,45 | 3,71 | 5,96 | 23 | 2,07 | 2,81 | 3,77 |
| 7 | 2,37 | 3,50 | 5,41 | 24 | 2,06 | 2,80 | 3,75 |
| 8 | 2,31 | 3,36 | 5,04 | 25 | 2,06 | 2,79 | 3,73 |
| 9 | 2,26 | 3,25 | 4,78 | 26 | 2,06 | 2,78 | 3,71 |
| 10 | 2,23 | 3,17 | 4,59 | 27 | 2,05 | 2,77 | 3,69 |
| 11 | 2,20 | 3,11 | 4,44 | 28 | 2,05 | 2,76 | 3,67 |
| 12 | 2,18 | 3,05 | 4,32 | 29 | 2,05 | 2,76 | 3,66 |
| 13 | 2,16 | 3,01 | 4,22 | 30 | 2,04 | 2,75 | 3,65 |
| 14 | 2,14 | 2,98 | 4,14 | 40 | 2,02 | 2,70 | 3,55 |
| 15 | 2,13 | 2,95 | 4,07 | 60 | 2,00 | 2,66 | 3,46 |
| 16 | 2,12 | 2,92 | 4,02 | 120 | 1,98 | 2,62 | 3,37 |
| 17 | 2,11 | 2,90 | 3,97 | ∞ | 1,96 | 2,58 | 3,29 |
| Р | 0,05 | 0,01 | 0,001 | 0,05 | 0,01 | 0,001 | |
|
|
|
(Цитировано по П.Ф. Рокицкому (1961), И.Ф. Правдину (1966), Г.Ф. Лакину (1980))
О некоторых требованиях к средним в рыбохозяйственных исследованиях
(По С.В. Козлитиной, 1969)
Средняя величина может быть надежным и объективным показателем лишь тогда, когда при ее вычислении соблюдаются определенные правила.
К числу основных из них можно отнести следующие:
1) Однородность изучаемого материала, которая достигается путем использования данных, относящихся к районам или водоемам с незначительными пространственными контрастами, в случае значительных контрастов необходимо выделять районы с характерными концепциями.
2) Исключение систематических ошибок, к которым относятся в основном инструментальные ошибки, влияющие более или менее одинаково на весь ряд наблюдений. Устранить эти ошибки можно только путем введения поправок. Например при определении численности рыб в море, вводится поправка на уловистость орудий лова.
3) Грубые ошибки. Поскольку все измерения представляют собой ограниченную выборку из генеральной совокупности и в выборку может попасть величина, частота которой невелика. И хотя ее появление возможно принимать в расчеты наравне со всеми остальными величинами неправомерно, так как вероятность такой величины близка к нулю. Обычно применяют критерий, позволяющий установить принадлежность случайной величины к рассматриваемой совокупности; это правило трех сигм. Если известна величина и среднеквадратическое отклонение одного измерения, то находят приближенную ошибку каждого измерения, то есть отклонения измеренной величины от средней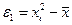 
. Обычно считают маловероятным, чтобы модуль ошибки превышал три сигмы.
Поэтому если найдется какое-нибудь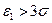 
, то соответствующее измерение считается содержащим грубую ошибку и отбрасывается.
|
|
|
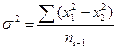(12)
4) существуют случайные ошибки, исключить которые невозможно, но можно учесть как погрешность наблюдения, так как случайные ошибки подчиняются нормальному закону распределения. На практике процесс обработки считается законченным, если подсчитана средняя квадратическая ошибка среднего арифметического 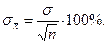(13)
(13)
При записи среднего арифметического принято указывать среднеквадратическую ошибку, обычно выражаемую в процентах.
Расчеты по выше указанным методам и формулам можно производить с помощью вычислительной техники (ЭВМ), используя методы современного программирования (листинг 1).
Листинг 1. Пример расчета средней с помощью языка программирования Pascal
Program Statistica;
var A: array [1..100] of real;
Y,S,Sa,Sko,D,Osa,Kv: real;
i,N: integer;
begin
writeln('Расчет статистических характеристик ряда');
write('Количество данных: '); readln(N);
writeln('Введите данные:');
writeln('N п/п данные');
for i:=1 to N do begin
write(i:3,' ');
readln(A[i])
end;
S:=0;
for i:=1 to M do S:=S+A[i];
Sa:=S/N;
S:=0;
for i:=1 to N do S:=S+sqr(A[i]-Sa);
D:=S/N;
Sko:=sqrt(D);
Osa:=Sko/sqrt(N);
Kv:=Sko/Sa;
writeln('Среднее арифметическое=',SA:8:1);
writeln('Ошибка средней=',Osa:8:1);
writeln('Дисперсия=',D:8:1);
writeln('Среднее квадратическое отклонение=',Sko:8:1);
writeln('Коэффициент вариации=',Kv:8:1);
readln
end.
Контрольные вопросы и задания
1. Дать понятие моде и медиане, средней арифметической и среднегеометрической величинам.
2. Измерение вариаций, вариационного размаха и средних отклонений: вариансы, среднеквадратического отклонения и стандартного отклонения (сигмы).
3. Оценка достоверности собранного материала, критерии достоверности.
4. Ошибки (систематические, грубые, случайные) при выполнении вариационно-статистичеких расчетах.
