Лекция 5.
Основные теоремы дифференциального исчисления.
Теорема Ферма. Пусть функция 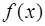 определена на интервале
определена на интервале 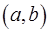 и в некоторой точке
и в некоторой точке 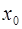 этого интервала принимает наибольшее или наименьшее значение. Тогда, если в точке
этого интервала принимает наибольшее или наименьшее значение. Тогда, если в точке 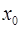 существует конечная производная, то она равна нулю.
существует конечная производная, то она равна нулю.
Теорема Ролля. Пусть на 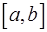 определена функция
определена функция 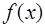 , причем:
, причем:
1) 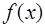 непрерывна на непрерывна на 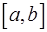 , ,
|
2) 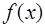 дифференцируема на дифференцируема на 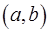 , ,
|
3) 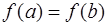 . .
|
Тогда существует точка 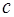 такая что
такая что 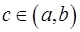 , и
, и 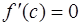 .
.
Теорема Лагранжа. Пусть на 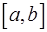 определена функция
определена функция 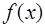 , причем:
, причем:
1) 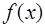 непрерывна на непрерывна на 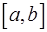 , ,
|
2) 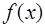 дифференцируема на дифференцируема на 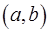 . .
|
Тогда существует точка 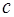 такая что
такая что 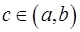 , и
, и 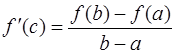 .
.
Формула Лагранжа. Равенство
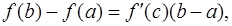
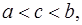
называется формулой Лагранжа, или формулой конечных приращений.
Теорема Коши. Пусть:
1) 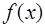 , , 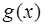 непрерывна на непрерывна на 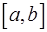 , ,
|
2) 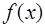 , , 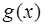 дифференцируема на дифференцируема на 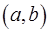 , ,
|
3) 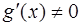 на на 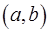 . .
|
Тогда существует точка 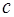 такая, что
такая, что 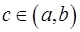 и справедлива формула:
и справедлива формула:
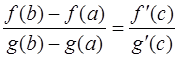 .
.
Раскрытие неопределенностей. Правило Лопиталя.
Определение. Будем говорить, что отношение двух функций 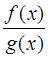 при
при 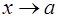 есть неопределенность вида
есть неопределенность вида 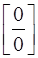 , если
, если 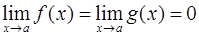 . Раскрыть эту неопределенность – означает вычислить предел
. Раскрыть эту неопределенность – означает вычислить предел 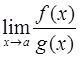 , если он существует, или установить, что он не существует.
, если он существует, или установить, что он не существует.
Теорема Лопиталя. Пусть функции 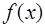 и
и 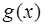 определены и дифференцируемы в некоторой окрестности точки
определены и дифференцируемы в некоторой окрестности точки 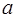 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки 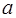 . Пусть также
. Пусть также 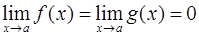 и
и 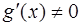 в указанной окрестности точки
в указанной окрестности точки 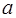 . Тогда, если существует предел отношения
. Тогда, если существует предел отношения 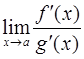 , то существует и предел
, то существует и предел 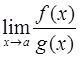 , причем справедливо соотношение
, причем справедливо соотношение
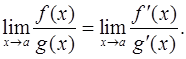
Rem.1. Теорема остается справедливой в случае когда 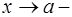 и
и 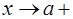 .
.
Rem.2. Если производные 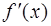 и
и 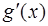 также удовлетворяют условиям теоремы Лопиталя, то теорему можно применять повторно:
также удовлетворяют условиям теоремы Лопиталя, то теорему можно применять повторно: 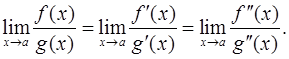
Rem.3. Теорема остается верной и в случае, когда 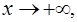
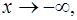
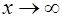 .
.
Определение. Будем говорить, что отношение двух функций 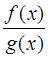 при
при 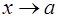 есть неопределенность вида
есть неопределенность вида 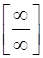 , если
, если
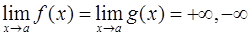 или
или 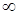 .
.
Для раскрытия этой неопределенности справедливо утверждение, аналогичное теореме Лопиталя, а именно: если в формулировке теоремы изменить условие на 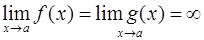 , то теорема останется справедливой.
, то теорема останется справедливой.
Неопределенности вида 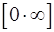 и
и 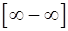 можно свести к неопределенности
можно свести к неопределенности 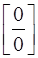 или к
или к 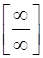 .
.
Формула Тейлора.
Теорема Тейлора. Пусть функция 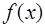 имеет в точке
имеет в точке 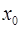 и некоторой ее окрестности производные порядка
и некоторой ее окрестности производные порядка 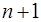 . Пусть
. Пусть 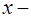 любое значение аргумента из указанной окрестности. Тогда между точками
любое значение аргумента из указанной окрестности. Тогда между точками 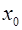 и
и 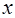 найдется точка
найдется точка 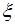 такая, что справедлива формула Тейлора:
такая, что справедлива формула Тейлора:
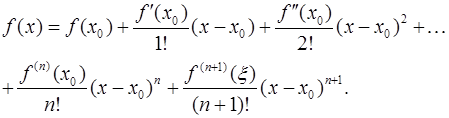
Формула Лагранжа.
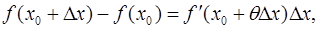
 .
.
Формула Маклорена. Формулу Тейлора при 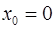 называют формулой Маклорена:
называют формулой Маклорена:
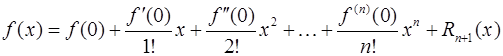 .
.
Остаточный член имеет вид
1. в форме Лагранжа: 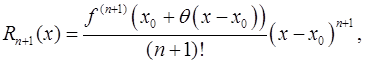
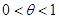 ;
;
2. в форме Пеано: 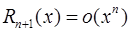 .
.
Геометрическое исследование поведения функции.
· Признак монотонности функции.
Если функция 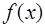 дифференцируема на интервале
дифференцируема на интервале 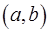 и
и 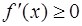 , то функция
, то функция 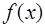 не убывает на
не убывает на 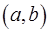 .
.
Если функция 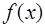 дифференцируема на интервале
дифференцируема на интервале 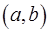 и
и 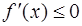 , то функция
, то функция 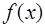 не возрастает на
не возрастает на 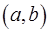 .
.
Если функция 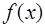 дифференцируема на интервале
дифференцируема на интервале 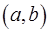 и
и 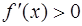 , то функция
, то функция 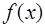 возрастает на
возрастает на 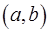 .
.
Если функция 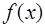 дифференцируема на интервале
дифференцируема на интервале 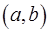 и
и 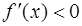 , то функция
, то функция 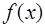 убывает на
убывает на 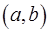 .
.
· Отыскание точек локального экстремума.
Определение. Точка 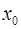 называется точкой строгого локального максимума функции
называется точкой строгого локального максимума функции 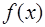 если для всех
если для всех 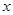 из некоторой
из некоторой 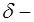 окрестности точки
окрестности точки 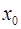 выполняется неравенство
выполняется неравенство 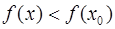 при
при 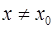 .
.
Определение. Точка 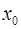 называется точкой строгого локального минимума функции
называется точкой строгого локального минимума функции 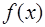 если для всех
если для всех 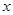 из некоторой
из некоторой 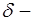 окрестности точки
окрестности точки 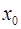 выполняется неравенство
выполняется неравенство 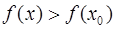 при
при 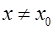 .
.
Необходимое условие локального экстремума. Если функция 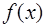 имеет в точке
имеет в точке 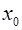 локальный экстремум и дифференцируема в этой точке, то
локальный экстремум и дифференцируема в этой точке, то 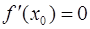 .
.
Геометрический смысл. Если точки 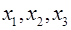 - точки локального экстремума и в этих точках существуют касательные к графику функции, то эти касательные параллельны оси
- точки локального экстремума и в этих точках существуют касательные к графику функции, то эти касательные параллельны оси 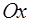 .
.
Точку 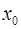 , для которой выполнено соотношение
, для которой выполнено соотношение 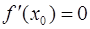 , называют точкой возможного экстремума.
, называют точкой возможного экстремума.
Достаточное условие локального экстремума. Пусть функция 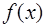 непрерывна в некоторой
непрерывна в некоторой 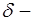 окрестности точки
окрестности точки 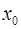 и дифференцируема в проколотой
и дифференцируема в проколотой 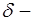 окрестности точки
окрестности точки 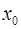 . Тогда:
. Тогда:
o если для всех 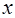 из левой
из левой 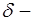 окрестности точки
окрестности точки 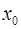
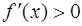 , а для всех
, а для всех 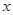 из правой
из правой 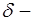 окрестности
окрестности 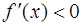 , то в точке
, то в точке 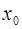 функция
функция 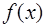 имеет локальный максимум;
имеет локальный максимум;
o если для всех 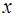 из левой
из левой 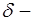 окрестности точки
окрестности точки 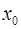
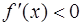 , а для всех
, а для всех 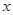 из правой
из правой 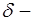 окрестности
окрестности 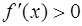 , то в точке
, то в точке 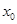 функция
функция 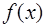 имеет локальный минимум;
имеет локальный минимум;
o если же 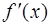 в
в 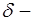 окрестности точки
окрестности точки 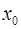 имеет один и тот же знак, то в точке
имеет один и тот же знак, то в точке 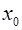 локального экстремума нет.
локального экстремума нет.
· Направление выпуклости и точки перегиба графика функции.
Определение. График функции 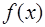 имеет на
имеет на 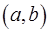 выпуклость направленную вниз, если он расположен не ниже любой касательной к графику функции на
выпуклость направленную вниз, если он расположен не ниже любой касательной к графику функции на 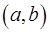 .
.
Определение. График функции 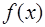 имеет на
имеет на 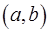 выпуклость направленную вверх, если он расположен не выше любой касательной к графику функции на
выпуклость направленную вверх, если он расположен не выше любой касательной к графику функции на 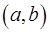 .
.
Достаточное условие выпуклости. Пустьфункция имеет на интервале 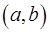 конечную
конечную 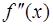 . Тогда:
. Тогда:
o если 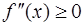 во всех точках
во всех точках 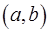 , то график функции
, то график функции 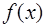 на
на 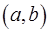 имеет выпуклость, направленную вниз;
имеет выпуклость, направленную вниз;
o если 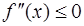 во всех точках
во всех точках 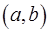 , то график функции
, то график функции 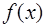 на
на 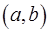 имеет выпуклость, направленную вверх.
имеет выпуклость, направленную вверх.
Определение. Точка 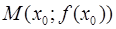 называется точкой перегиба графика функции
называется точкой перегиба графика функции 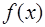 , если существует такая
, если существует такая 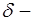 окрестность точки
окрестность точки 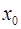 , в пределах которой график функции
, в пределах которой график функции 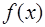 слева и справа от точки
слева и справа от точки 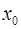 имеет разные направления выпуклости.
имеет разные направления выпуклости.
Необходимое условие точки перегиба. Пусть график функции 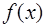 имеет перегиб в точке
имеет перегиб в точке 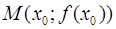 и пусть функция
и пусть функция 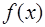 имеет в точке
имеет в точке 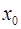 непрерывную вторую производную, тогда
непрерывную вторую производную, тогда 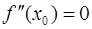 .
.
Определени е. Точка 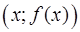 графика функции
графика функции 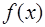 , для которой
, для которой 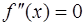 называется критической.
называется критической.
Достаточное условие точки перегиба. Пусть функция 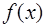 непрерывна, имеет конечную
непрерывна, имеет конечную 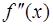 в некоторой проколотой
в некоторой проколотой 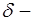 окрестности точки
окрестности точки 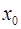 . Тогда, если в пределах указанной
. Тогда, если в пределах указанной 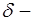 окрестности
окрестности 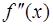 имеет разные знаки слева и справа от точки
имеет разные знаки слева и справа от точки 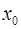 , то график функции
, то график функции 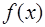 имеет перегиб в точке
имеет перегиб в точке 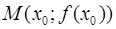 .
.
· Асимптоты графика функции. Прямая линия называется асимптотой для кривой 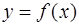 , если расстояние
, если расстояние 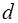 от точки
от точки 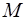 , лежащей на кривой, до прямой стремится к нулю при удалении точки
, лежащей на кривой, до прямой стремится к нулю при удалении точки 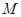 от начала координат в бесконечность.
от начала координат в бесконечность.
Определение. Прямая 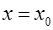 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 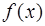 , если хотя бы один из пределов
, если хотя бы один из пределов 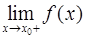 или
или 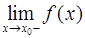 равен
равен 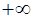 или
или 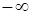 .
.
Определение. Прямая 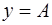 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 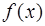 , при
, при 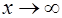 если хотя бы один из пределов
если хотя бы один из пределов 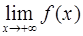 или
или 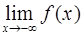 равен
равен 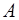 .
.
Определение. Прямая 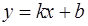 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 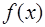 , при
, при 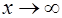 если существуют числа
если существуют числа 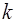 и
и 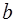 такие, что
такие, что 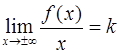 ,
, 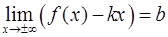 .
.
· Схема исследования графика функции.
1. Определить область существования функции.
2. Найти точки пересечения графика функции с осями координат.
3. Найти асимптоты.
4. Найти точки возможного экстремума.
5. Найти критические точки.
6. Провести исследование знака первой и второй производных. Определить участки возрастания, убывания и направления выпуклости, найти точки экстремумов и точки перегиба.
7. Построить график.
· Касательная к графику функции 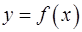 в точке
в точке 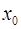
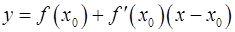 .
.
· Нормаль к графику функции 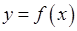 в точке
в точке 
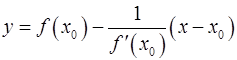 .
.
 2020-04-07
2020-04-07 228
228






