Вычисление несобственного интеграла 2-го рода

Случай функции с особой точкой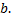

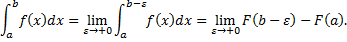
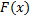 – первообразная для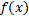

Таким образом, 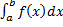 сходится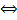 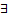 конечный предел первообразной .

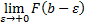Примеры.

 

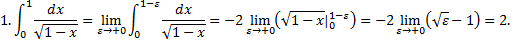
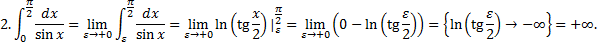
Рассмотрим интегралы

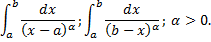
Рассмотрим случай интеграла с особой точкой в левом конце отрезка:

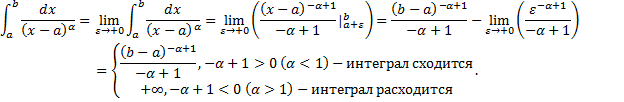
Случай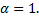

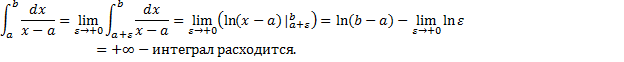
Аналогично рассматривается интеграл с особой точкой в правом конце отрезка. Таким образом

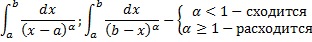
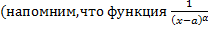 имеет при  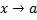порядок роста  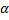относительно ).

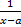Исследование несобственных интегралов 2-го рода на сходимость.

Признаки сходимости:

1. Признак сравнения:

пусть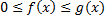

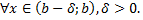
a. Если 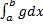 сходится, то  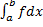также сходится.

b. Если 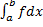 расходится, то  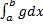также расходится.

2. Предельный признак сравнения.

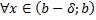
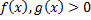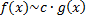Пусть для  и  при 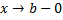, т.е. .

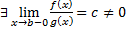Тогда 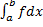 и 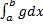 оба сходятся или оба расходятся.

3. Если сходится 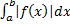, то сходится и  .

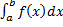Примеры.

1.

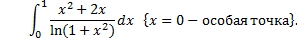
При ,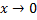

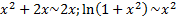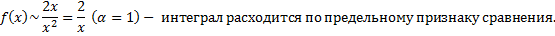
2.

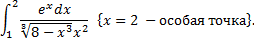
При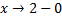

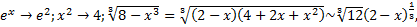
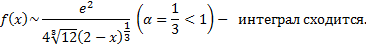
Замечание: если 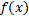 непрерывна на  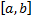кроме точк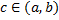и  и 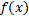 не ограничена в окрестности точки , тогда

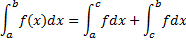
(для первого и второго интегралов в правой части особой точкой является 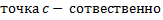  правый или левый конец отрезка).

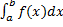 сходится  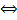сходятся оба интеграла  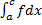и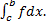

Пример.

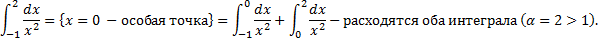
Примеры несобственных интегралов с несколькими особыми точками

1.

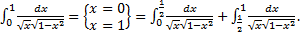
Исходный интеграл сходится, если сходятся оба интеграла в правой части:

a. .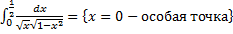

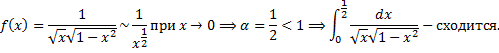
b. .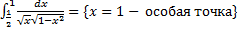

.

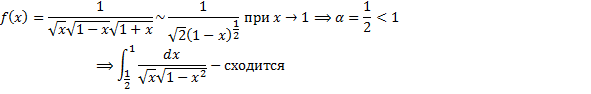
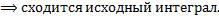
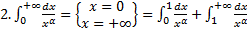(несобственный интеграл 2-го рода 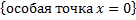+ несобственный интеграл 1-го рода ).

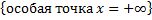a.  – сходится при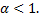

b. 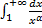 – сходится при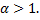

Значит, 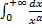 расходится для любого .

.

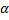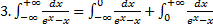a.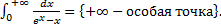

При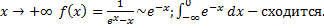

b.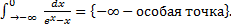

При .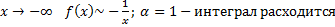

Таким образом исходный интеграл расходится.

Абсолютная и условная сходимость несобственных интегралов.

Рассмотрим несобственный интеграл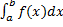

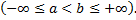
Опр. Несобственный интеграл 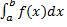называется абсолютно сходящимся, если сходится интеграл .

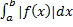Опр. Несобственный интеграл 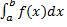называется условно сходящимся, если он сходится, но интеграл  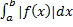расходится.

Пример.

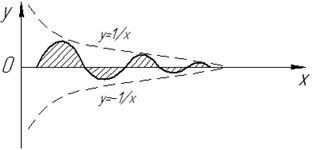
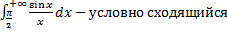 ( без доказательства, см. рис. 17).