Относительные показатели вариации

Тема 4.3. «Показатели вариации в статистике»

Вариация – называется изменчивость значений признака у единиц статистической совокупности.

Абсолютные показатели вариации.

1. Размах вариации – разность между максимальным и минимальным значениями признака

R=x_max - x_min

Характеризует максимальное различие крайних значений признака у единиц совокупности.

2. Средне-линейное отклонение – представляет собо среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признак от их среднего.

а) если ряд не сгруппирован, то для расчетов используется простая – невзвешенная формула:

б) Для вариационного интервального ряда с неразрывными частотами используют взвешенную формулу:

Если значительно меньше средней арифметической , то совокупность однородна и для нее типична.

3. Дисперсией называется средняя арифметическая величина из квадратов отклонений значений от их среднего.

а) простая

б) взвешенная

4. Среднее квадратическое отклонение – квадратный корень из дисперсии

Относительные показатели вариации.

Относительные показатели вариации используются для характеристики интенсивности вариации и сравнения ее величины по различным совокупностям

1. Коэффициент осцилляции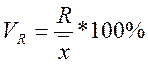

Характеризует относительную изменчивость крайних значений признака вокруг средней арифметической.

2. Линейный коэффициент вариации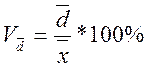

Характеризует долю усредненного значения абсолютных отклонений x_i от в средней величине признака.

3. Коэффициент вариации

Характеризует степень относительной колеблемости признака. Если V<33% - то совокупность однородна, колеблемость признака невысока и средняя арифметическая для нее типична.

Размер месячной заработной платы, руб	Число сотрудников, человек
4000 – 6000	10
6000 – 8000	6
8000 – 10000	19
10000 – 12000	26
12000 – 14000	19
14000 – 16000	10
16000 – 18000	5
ИТОГ

Пример:

Определить абсолютные и относительные показатели вариации.

Решение:

1. Рассчитаем среднюю величину, для этого используем среднее арифметическое взвешенной.

Для удобства построим дополнительные столбцы в таблице.

Размер месячной заработной платы, руб	Середины интервалов, x_i	Число сотрудников человек f_i	x_if_i*
4 000 – 6 000	5 000	10	50 000
6 000 – 8 000	7 000	6	42 000
8 000 – 10 000	9 000	19	171 000
10 000 – 12 000	11 000	26	286 000
12 000 – 14 000	13 000	19	247 000
14 000 – 16 000	15 000	10	150 000
16 000 – 18 000	17 000	5	85 000
ИТОГ		95	1 031 000

Вычисляем середины интервалов:

1 интервал: (4 000+6 000) / 2= 5 000

2 интервал: (6 000+8 000) / 2= 7 000

3 интервал: (8 000+10 000) / 2= 9 000

4 интервал: (10 000+12 000) / 2= 11 000

5 интервал: (12 000+14 000) / 2= 13 000

6 интервал: (14 000+16 000) / 2= 15 000

7 интервал: (16 000+18 000) / 2= 17 000

Вычисляем x_i*f_i:

1 интервал: 5 000 * 10 = 50 000

2 интервал: 7 000 * 6 = 42 000

3 интервал: 9 000 * 19 = 171 000

4 интервал: 11 000 * 26 = 286 000

5 интервал: 13 000 * 19 = 247 000

6 интервал: 15 000 * 10 = 150 000

7 интервал: 17 000 * 5 = 85 000

Среднее

Вывод: средняя заработная плата составляет – 10 853 рубля.

Абсолютные показатели вариации:

1. Размах вариации: R=x_max - x_min

x _max = 18 000 x_min = 4 000

R= 18 00 – 4 000 = 14 000

Вывод: разность между максимальным и минимальным размером заработной платы равна 14 000 рублей.

2. Средне-линейное отклонение

Размер месячной заработной платы, руб	Середины интервалов, x_i	Число сотрудников человек f_i
4 000 – 6 000	5 000	10	58 530
6 000 – 8 000	7 000	6	23 118
8 000 – 10 000	9 000	19	35 207
10 000 – 12 000	11 000	26	3 822
12 000 – 14 000	13 000	19	40 793
14 000 – 16 000	15 000	10	41 470
16 000 – 18 000	17 000	5	30 735
ИТОГ		95	233 675

Вычисляем :

1 интервал: ê5 000 – 10 853 ê* 10 = 58 530

2 интервал: ê7 000 – 10 853 ê* 6 = 23 118

3 интервал: ê9 000 – 10 853 ê* 19 = 35 207

4 интервал: ê11 000 – 10 853 ê* 26 = 3 822

5 интервал: ê13 000 – 10 853 ê* 19 = 40 793

6 интервал: ê15 000 – 10 853 ê* 10 = 41 470

7 интервал: ê17 000 – 10 853 ê * 5 = 30 735

3. Дисперсией

Размер месячной заработной платы, руб	Середины интервалов, x_i	Число сотрудников человек f_i
4 000 – 6 000	5 000	10	342 576 090
6 000 – 8 000	7 000	6	89 073 654
8 000 – 10 000	9 000	19	65 238 571
10 000 – 12 000	11 000	26	561 834
12 000 – 14 000	13 000	19	87 582 571
14 000 – 16 000	15 000	10	171 976 090
16 000 – 18 000	17 000	5	188 928 045
ИТОГ		95	945 936 855