Класифікатор тесту
Вища математика
Характеристичне рівняння д.р. з сталими коефіцієнтами
Інтегрування частинами
Поняття первісної
Умовний екстремум
Достатні умови екстремуму
Необхідні умови екстремуму
Визначення функціонального ряду
Частинні похідні вищих порядків
Геометричний і економічний зміст градієнта
Градієнт
Диференціал
Частинні похідні
Графік функції
Неперервність функції
Область визначення
Степеневі ряди
Правила інтегрування
Таблиця первісних
Заміна змінних у невизначеному інтегралі
Визначення числового ряду
Диференціальні рівняння з відокремлювани-ми змінними
Задача Коші
Визначення диференціального рівняння
Однорідні диференціальні рівняння
Невласні інтеграли
Застосування визначених інтегралів
Інтегрування частинами у визначеному інтегралі
Заміна змінних у визначеному інтегралі
Формула Ньютона –Лейбніца
Визначений інтеграл та його властивості
Інтегрування ірраціональних виразів
Інтегрування тригонометричних виразів
Інтегрування дробів
Збіжність числового ряду
Загальний розв'язок однорідного д.р. з сталими коефіцієнтами
Тестові завдання
Тема: "Характеристичне рівняння д.р. з сталими коефіцієнтами" (3)
1 (1).
Запитання:
ОДНА ПРАВИЛЬНА ВІДПОВІДЬ. Який вигляд має характеристичне рівняння лінійного д.р. з сталими коефіцієнтами

2 (2).
Запитання:
ОДНА ПРАВИЛЬНА ВІДПОВІДЬ. Який вигляд має характеристичне рівняння лінійного д.р. з сталими коефіцієнтами
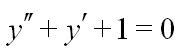
3 (3).
Запитання:
ОДНА ПРАВИЛЬНА ВІДПОВІДЬ. Який вигляд має характеристичне рівняння лінійного д.р. з сталими коефіцієнтами
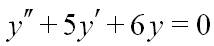
Тема: "Інтегрування частинами" (3)
1 (4).
Запитання:
Чи вірно застосували інтегрування частинами до інтегралу?
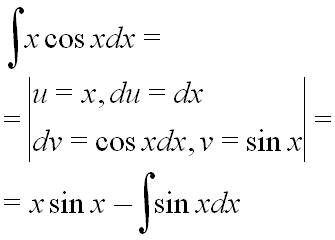
2 (5).
Запитання:
Чи вірно застосували інтегрування частинами до інтегралу?
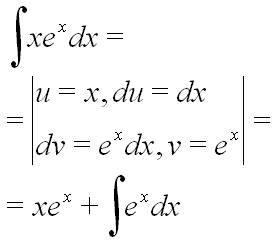
3 (6).
Запитання:
Чи вірно застосували інтегрування частинами до інтегралу?
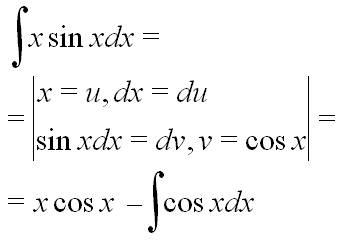
Тема: "Поняття первісної" (3)
1 (7).
Запитання:
Чи є функція (2cos2x+3)первісною функції (-4sin2x)?
2 (8).
Запитання:
Чи є функція

3 (9).
Запитання:
Чи є функція
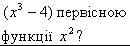
Тема: "Умовний екстремум" (3)
1 (10).
Запитання:
ОДНА ПРАВИЛЬНА ВІДПОВІДЬ. Який вигляд для задачі умовного екстремуму z=f(x,y), g(x,y)=C має функція Лагранжа
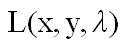
2 (11).
Запитання:
ОДНА ПРАВИЛЬНА ВІДПОВІДЬ. Який вигляд має функція Лагранжа L для задачі умовного екстремуму
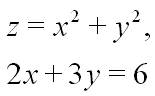
3 (12).
Запитання:
 2020-04-12
2020-04-12 95
95







