5.1.Условие потенциальности электрического поля.
Электрическое поле точечного заряда является потенциальным полем. Действительно, согласно формуле (3) напряженность электрического поля точечного заряда
E 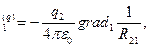
поэтому 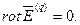
Электрическое поле любой системы зарядов является потенциальным, потому что оно получается наложением полей отдельных точечных зарядов, составляющих эту систему:
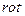 E
E 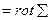 E
E 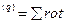 E
E 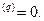
Согласно теореме Стокса поток ротора векторного поля сквозь любую поверхность равен циркуляции этого поля по линии, ограничивающей поверхность. Так как 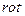 E
E 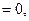 то
то
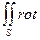 En
En 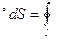 El
El 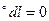
При вычислении циркуляции (криволинейного интеграла по замкнутому контуру) интегрируется касательная составляющая напряжённости электрического поля 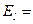 El
El 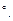 Направление нормали n
Направление нормали n 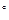 к поверхности
к поверхности 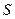 и направление обхода контура
и направление обхода контура 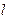 , заданное единичным вектором l
, заданное единичным вектором l 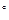 , касательным к линии
, касательным к линии 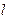 , связаны правилом правого винта (рис. 5).
, связаны правилом правого винта (рис. 5).
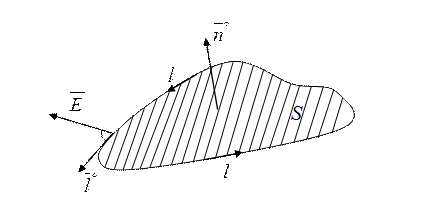
Рис. 5.Правовинтовая система координат, связанная с контуром 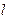
Равенства 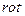 E
E 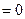 (6)
(6)
и 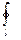 El
El 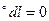 (7)
(7)
называются условием потенциальности электрического поля в дифференциальной и интегральной форме соответственно.
5.2. Электрический потенциал точечного заряда. Электрический потенциал вводится формулой
E 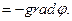 (8)
(8)
При этом условие 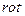 E
E 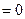 выполняется автоматически.
выполняется автоматически.
Сравнивая последнее выражение для напряженности электрического поля с выражением для напряженности точечного заряда (3), находим, что электрическое поле точечного заряда обладает потенциалом
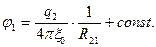 (9)
(9)
Если принять, что на бесконечности потенциал равен нулю, то произвольная постоянная в последней формуле равна нулю.
5.3. Электрический потенциал пространственного распределения зарядов. Пусть внутри заряженного тела, занимающего в пространстве ограниченный объём 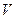 , заряд распределен с известной плотностью ρ. Напряжённость электрического поля, созданного этим телом, можно определить по первой из формул (5), которая допускает и другие представления:
, заряд распределен с известной плотностью ρ. Напряжённость электрического поля, созданного этим телом, можно определить по первой из формул (5), которая допускает и другие представления:
E 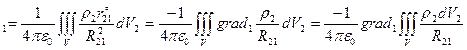 .
.
Сравнивая последнее выражение с формулой (8) E 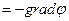 , находим, что электрический потенциал заряженного тела равен
, находим, что электрический потенциал заряженного тела равен
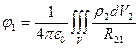 . (10)
. (10)
Это же представление потенциала можно получить из формулы (9) с помощью принципа наложения. В последней формуле опущена аддитивная постоянная, это равносильно тому, что точка нулевого потенциала выбрана на бесконечности.
В математической физике функцию 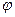 , определённую по формуле (10) (исключая
, определённую по формуле (10) (исключая 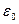 ), называют объёмным потенциалом. Внутри объёма
), называют объёмным потенциалом. Внутри объёма 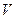 потенциал имеет интегрируемую особенность и непрерывные пространственные производные, которые представляют собой проекции вектора напряжённости электрического поля на оси координат (с противоположным знаком).
потенциал имеет интегрируемую особенность и непрерывные пространственные производные, которые представляют собой проекции вектора напряжённости электрического поля на оси координат (с противоположным знаком).
По аналогии с объёмным потенциалом можно найти потенциал заряженной поверхности 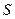 и заряженной линии
и заряженной линии 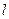 :
:
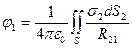 ,
, 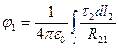 . (11)
. (11)
В математической физике первый интеграл называется потенциалом простого слоя (исключая 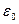 ). В точках поверхности
). В точках поверхности 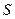 он непрерывен, так как площадь элемента
он непрерывен, так как площадь элемента 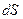 убывает пропорционально
убывает пропорционально 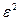 , а знаменатель подынтегральной функции уменьшается пропорционально
, а знаменатель подынтегральной функции уменьшается пропорционально 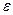 , значит, величина интеграла по окрестности особой точки убывает пропорционально
, значит, величина интеграла по окрестности особой точки убывает пропорционально 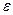 , где
, где 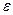 -размер (радиус) этой окрестности. Во второй из формул (5) размер особенности пропорционален
-размер (радиус) этой окрестности. Во второй из формул (5) размер особенности пропорционален 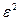 и знаменатель подынтегральной функции
и знаменатель подынтегральной функции 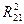 пропорционален
пропорционален 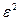 , поэтому, вообще говоря, проекции вектора напряженности на заряженной поверхности имеют разрывы. Более точная формулировка гласит, что нормальная составляющая напряженности изменяется на поверхности
, поэтому, вообще говоря, проекции вектора напряженности на заряженной поверхности имеют разрывы. Более точная формулировка гласит, что нормальная составляющая напряженности изменяется на поверхности 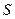 скачком, а касательная составляющая непрерывна.
скачком, а касательная составляющая непрерывна.
Изучение электрического поля скалярной функции 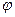 вместо векторной функции E существенно упрощает теорию. Значительно уменьшается объём вычислений при расчёте полей, в частности, при численном интегрировании формул (10) и (11) вместо формул (5).
вместо векторной функции E существенно упрощает теорию. Значительно уменьшается объём вычислений при расчёте полей, в частности, при численном интегрировании формул (10) и (11) вместо формул (5).
Пример 1. Вернемся, к примеру, рассмотренному в §4 (рис.4). Определим электрический потенциал на оси диска радиуса 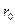 , равномерно заряженного с помощью
, равномерно заряженного с помощью 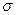 . Согласно первой из формул (11)
. Согласно первой из формул (11)
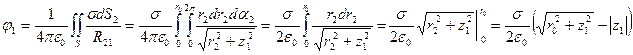 На поверхности диска (
На поверхности диска (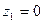 ) потенциал равен
) потенциал равен
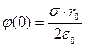 .
.
Напряженность электрического поля на оси OZ равна
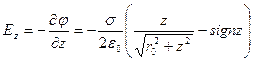 ,
,
где 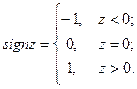
Это выражение для напряженности с несущественным различием в обозначениях совпадает с формулой, полученной в примере из §4. Здесь функция 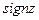 подчёркивает скачок нормальной составляющей напряженности на поверхности диска.
подчёркивает скачок нормальной составляющей напряженности на поверхности диска.
В приведённом здесь расчёте в неявном виде содержится выражение для потенциала на оси заряжённой окружности, скажем, радиуса 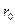 . Чтобы записать это выражение, нужно исключить интегрирование по
. Чтобы записать это выражение, нужно исключить интегрирование по 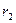 и заменить
и заменить 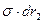 на
на 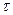 -линейную плотность заряда на окружности:
-линейную плотность заряда на окружности:
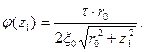
В частности, в центре окружности (при 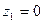 )
) 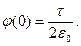
Пример 2. Определим электрический потенциал окружности радиуса 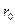 , заряженной с линейной плотностью
, заряженной с линейной плотностью 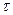 , в плоскости этой окружности. Электрическое поле обладает осью симметрии, перпендикулярной плоскости окружности. Направим ось OZ цилиндрической системы координат по оси симметрии поля. Потенциал не зависит от угла поворота вокруг этой оси, т.е.
, в плоскости этой окружности. Электрическое поле обладает осью симметрии, перпендикулярной плоскости окружности. Направим ось OZ цилиндрической системы координат по оси симметрии поля. Потенциал не зависит от угла поворота вокруг этой оси, т.е. 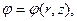 а в плоскости
а в плоскости 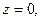 в которой расположена окружность,
в которой расположена окружность, 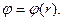 Точку наблюдения 1 поместим на ось Or, где
Точку наблюдения 1 поместим на ось Or, где 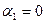 (рис.6).
(рис.6).
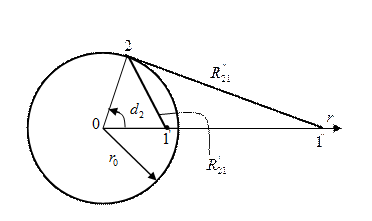
Рис.6. Заряженная окружность в плоскости 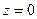 цилиндрической системы координат (два варианта выбора точки наблюдения 1)
цилиндрической системы координат (два варианта выбора точки наблюдения 1)
Согласно второй из формул (11)
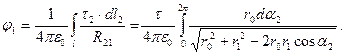
Расстояние между точками 2 и 1 определено с помощью теоремы косинусов для треугольника 012. Вследствие симметрии контура интегрирования относительно точки наблюдения последний интеграл равен удвоенному интегралу от той же самой функции в пределах от 0 до 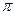 . Далее преобразуем подкоренное выражение
. Далее преобразуем подкоренное выражение
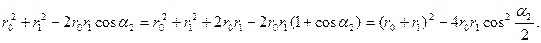
После замены переменной интегрирования 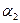 на
на 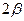 пределы интегрирования будут равны 0 и
пределы интегрирования будут равны 0 и 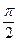 :
:
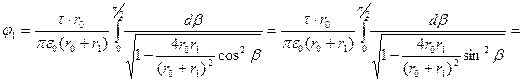

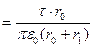 К (к),
К (к),
где К (к) - полный эллиптический интеграл первого рода модуля 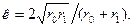 В центре окружности
В центре окружности 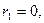
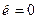 , К (0)
, К (0) 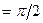 , следовательно,
, следовательно, 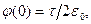 как в конце примера 1. При
как в конце примера 1. При 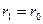
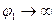 .
.
Вычисление полных эллиптических интегралов с помощью рядов или рекуррентных формул не менее трудоёмко, чем численное интегрирование по переменной 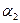 в исходной формуле для потенциала. Принципиальный график изменения электрического потенциала в плоскости заряженной окружности показан на рис.7.
в исходной формуле для потенциала. Принципиальный график изменения электрического потенциала в плоскости заряженной окружности показан на рис.7.
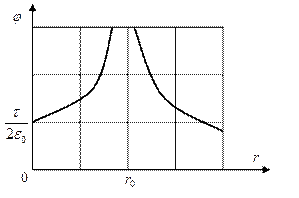
Рис.7. График потенциала 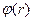 в плоскости
в плоскости 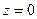
 2020-04-07
2020-04-07 342
342







