НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ПЛАН ЛЕКЦИИ
I. Функция распределения вероятностей непрерывной случайной величины
II. Плотность распределения вероятностей непрерывной случайной величины
III. Числовые характеристики непрерывных случайных величин
IV. Законы распределения непрерывных случайных величин
I. Функция распределения вероятностей непрерывной случайной величины. Непрерывной называется случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.
Непрерывная случайная величина в отличие от дискретной не может быть задана перечнем всех ее возможных значений и их вероятностей. Для задания случайных величин любого типа (дискретных и непрерывных) вводятся функции распределения вероятностей случайных величин.
Пусть 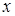 – действительное число. Вероятность того, что случайная величина
– действительное число. Вероятность того, что случайная величина 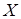 примет значение, меньшее
примет значение, меньшее 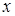 , то есть вероятность события
, то есть вероятность события 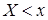 , обозначим
, обозначим 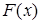 .
.
Функцией распределения называется функция 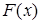 , определяющая вероятность того, что случайная величина
, определяющая вероятность того, что случайная величина 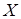 примет значение, меньшее
примет значение, меньшее 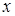 , то есть
, то есть
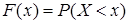 . (1)
. (1)
Геометрический смысл этого равенства следующий: 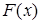 – это вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки
– это вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки 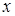 .
.
Определение функции распределения справедливо и для дискретных, и для непрерывных случайных величин
Пример 1. Монета брошена 2 раза. Найти функцию распределения случайной величины 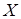 – числа выпадений герба – и построить ее график.
– числа выпадений герба – и построить ее график.
Решение. Случайная величина 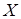 – число выпадений герба – распределена по биномиальному закону. Закон распределения этой случайной величины имеет вид
– число выпадений герба – распределена по биномиальному закону. Закон распределения этой случайной величины имеет вид
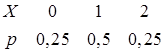
Найдем функцию распределения случайной величины 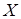 по определению, используя формулу (1). Если
по определению, используя формулу (1). Если 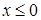 , то
, то 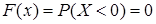 , так как случайная величина
, так как случайная величина 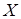 не имеет отрицательных возможных значений. Если
не имеет отрицательных возможных значений. Если 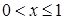 , то
, то 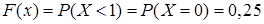 , так как
, так как 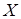 может принять значение 0. Если
может принять значение 0. Если 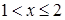 , то
, то 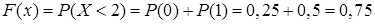 , так как
, так как 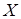 может принять значения 0 или 1, причем эти события несовместны. Если
может принять значения 0 или 1, причем эти события несовместны. Если 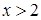 , то в этом случае
, то в этом случае 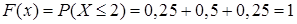 . Функция распределения имеет вид
. Функция распределения имеет вид
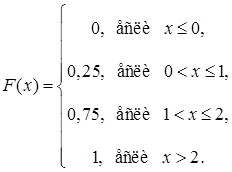
Построим график этой функции.
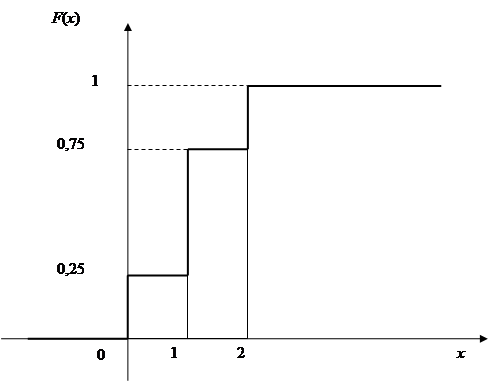
График функции распределения дискретной случайной величины
Случайная величина называется непрерывной, если ее функция распределения является непрерывной, кусочно-дифференцируемой функцией с непрерывной производной.
Свойства функции распределения:
1) значения функции распределения принадлежат отрезку 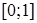 ,
,
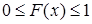 ; (2)
; (2)
2) 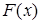 – неубывающая функция, то есть
– неубывающая функция, то есть 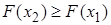 , если
, если 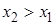 .
.
Следствия свойства 2:
а) вероятность того, что случайная величина 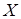 примет значение, заключенное в интервале
примет значение, заключенное в интервале 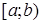 , равна приращению функции распределения на этом интервале,
, равна приращению функции распределения на этом интервале,
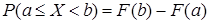 ; (3)
; (3)
б) вероятность того, что непрерывная случайная величина 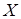 примет одно определенное значение, равна нулю,
примет одно определенное значение, равна нулю,
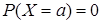 ; (4)
; (4)
3) если возможные значения случайной величины 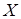 принадлежат интервалу
принадлежат интервалу 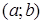 , то
, то 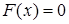 при
при 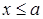 ,
, 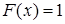 при
при 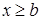 .
.
Следствие свойства 3: если возможные значения непрерывной случайной величины 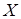 расположены на всей оси
расположены на всей оси 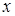 , то справедливы предельные соотношения
, то справедливы предельные соотношения
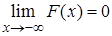 ,
, 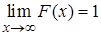 . (5)
. (5)
II. Плотность распределения вероятностей непрерывной случайной величины. Непрерывную случайную величину можно также задать, используя другую функцию, которая называется плотностью распределения или плотностью вероятности.
Плотностью распределения вероятностей непрерывной случайной величины 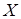 называется функция
называется функция 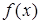 – первая производная от функции распределения
– первая производная от функции распределения 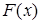 :
:
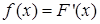 . (6)
. (6)
Теорема 1: вероятность того, что непрерывная случайная величина 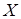 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 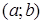 , равна определенному интегралу от плотности распределения, взятому в пределах от
, равна определенному интегралу от плотности распределения, взятому в пределах от 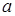 до
до 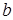 ,
,
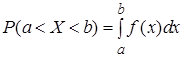 . (7)
. (7)
Доказательство.
Используем следствие а) свойства 2 функции распределения:
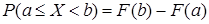 .
.
Вычислим определенный интеграл (7) по формуле Ньютона–Лейбница, используя определение (6),
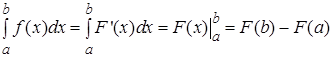 .
.
Тогда
 . (8)
. (8)
События 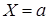 и
и 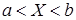 несовместные, поэтому по теореме сложения вероятностей несовместных событий
несовместные, поэтому по теореме сложения вероятностей несовместных событий
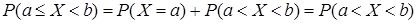 ,
,
так как 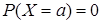 (следствие б) свойства 2 функции распределения). Подставляя последнее равенство в левую часть выражения (8), получим
(следствие б) свойства 2 функции распределения). Подставляя последнее равенство в левую часть выражения (8), получим
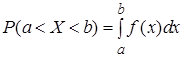 .
.
Теорема доказана.
Геометрический смысл этой теоремы следующий: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу 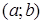 , равна площади криволинейной трапеции, ограниченной осью О
, равна площади криволинейной трапеции, ограниченной осью О 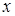 , графиком плотности распределения
, графиком плотности распределения 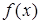 и прямыми
и прямыми 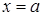 ,
, 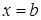 .
.
Зная плотность распределения 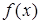 , можно найти функцию распределения по формуле
, можно найти функцию распределения по формуле
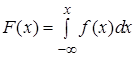 . (9)
. (9)
Свойства плотности распределения:
1) плотность распределения – неотрицательная функция, 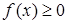 , так как функция распределения
, так как функция распределения 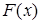 – неубывающая. Это означает, что точки, принадлежащие графику плотности распределения, расположены или над осью
– неубывающая. Это означает, что точки, принадлежащие графику плотности распределения, расположены или над осью 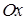 , или на этой оси. График плотности распределения называется кривой распределения;
, или на этой оси. График плотности распределения называется кривой распределения;
2) несобственный интеграл от плотности распределения в пределах от 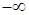 до
до 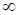 равен единице,
равен единице,
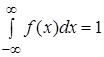 . (10)
. (10)
Выражение (10) называется также условием нормировки.
III. Числовые характеристики непрерывных случайных величин. Определения числовых характеристик дискретных случайных величин распространяются на непрерывные величины.
Математическим ожиданием непрерывной случайной величины 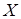 , возможные значения которой принадлежат отрезку
, возможные значения которой принадлежат отрезку 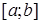 , называется определенный интеграл
, называется определенный интеграл
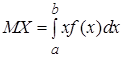 . (11)
. (11)
Если возможные значения непрерывной случайной величины принадлежат всей оси 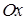 , то
, то
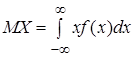 . (12)
. (12)
Предполагается, что этот несобственный интеграл сходится абсолютно, то есть существует конечный интеграл 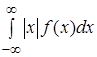 .
.
Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
Если возможные значения 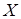 принадлежат отрезку
принадлежат отрезку 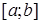 , то
, то
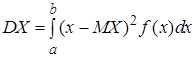 . (13)
. (13)
Если возможные значения непрерывной случайной величины принадлежат всей оси 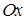 , то
, то
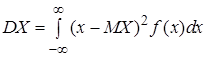 . (14)
. (14)
Для вычисления дисперсии существуют более удобные формулы:
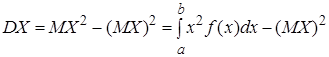 (15)
(15)
или
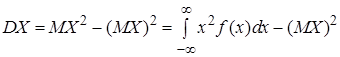 . (16)
. (16)
Среднее квадратическое отклонение непрерывной случайной величины определяется выражением
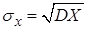 . (17)
. (17)
Свойства математического ожидания и дисперсии, указанные для дискретных случайных величин, сохраняются и для непрерывных величин.
IV. Законы распределения непрерывных случайных величин. Рассмотрим основные законы распределения непрерывных случайных величин.
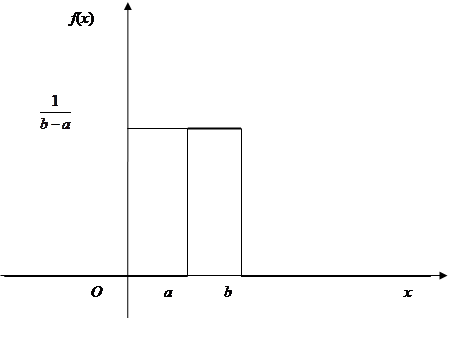
Равномерный закон распределения. Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Найдем плотность равномерного распределения 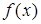 ,
,
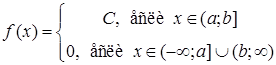 .
.
Константу 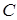 найдем из условия
найдем из условия 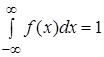 . Для равномерного закона
. Для равномерного закона
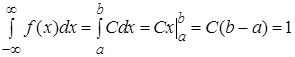 , откуда
, откуда 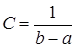 . Тогда
. Тогда
 |
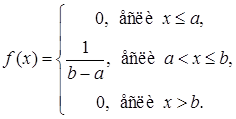 (18)
(18)
График плотности равномерного распределения
Найдем функцию равномерного распределения 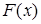 по формуле (9)
по формуле (9)
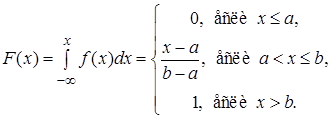 (19)
(19)
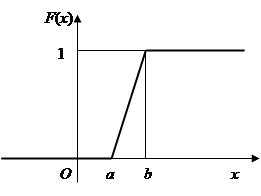
График функции равномерного распределения
Найдем числовые характеристики равномерно распределенной случайной величины. Математическое ожидание по формуле (11)
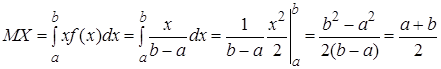 . (20)
. (20)
Дисперсия по формуле (15)
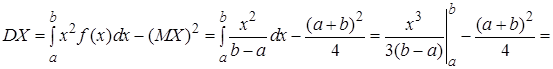 (21)
(21)
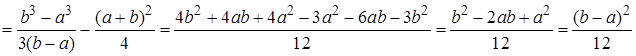 .
.
Среднее квадратическое отклонение по формуле (17)
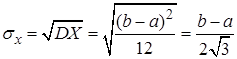 . (22)
. (22)
Нормальный закон распределения. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью
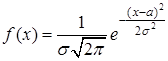 . (23)
. (23)
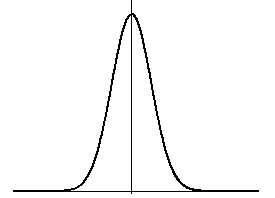
График плотности нормального распределения
Нормальное распределение определяется двумя параметрами: 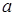 и
и 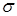 .
.
График плотности нормального распределения называется нормальной кривой (или кривой Гаусса). Функция (23) определена на всей оси 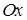 . При всех значениях
. При всех значениях 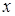
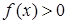 , то есть нормальная кривая расположена над осью
, то есть нормальная кривая расположена над осью 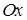 .
. 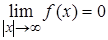 , значит, ось
, значит, ось 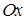 является горизонтальной асимптотой графика. Исследуем функцию на экстремум,
является горизонтальной асимптотой графика. Исследуем функцию на экстремум, 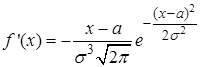 ,
, 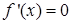 при
при 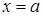 ,
, 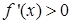 при
при 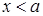 ,
, 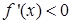 при
при 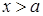 . При
. При 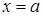 функция
функция 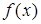 имеет максимум, равный
имеет максимум, равный 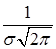 . График функции симметричен относительно прямой
. График функции симметричен относительно прямой 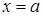 .
.
Изменение величины параметра 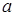 не изменяет форму нормальной кривой, а только приводит к ее сдвигу вдоль оси
не изменяет форму нормальной кривой, а только приводит к ее сдвигу вдоль оси 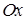 вправо, если
вправо, если 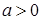 , и влево, если
, и влево, если 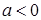 .
.
С возрастанием значения 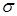 максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, то есть прижимается к оси
максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, то есть прижимается к оси 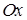 . При уменьшении
. При уменьшении 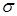 нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси
нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси 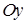 .
.
Найдем числовые характеристики нормально распределенной случайной величины. Математическое ожидание по формуле (12)
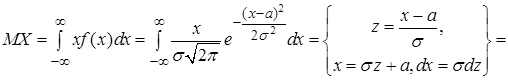 (24)
(24)
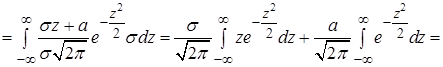
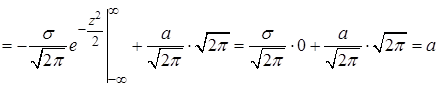 ,
,
так как 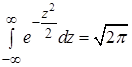 – интеграл Пуассона.
– интеграл Пуассона.
Таким образом, математическое ожидание нормально распределенной случайной величины равно параметру 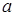 .
.
Дисперсия по формуле (14)
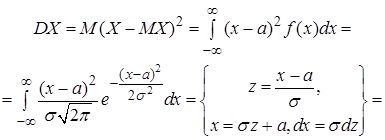
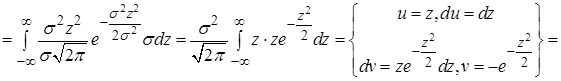
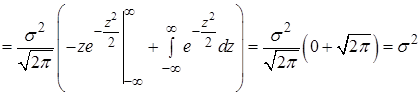 . (25)
. (25)
Среднее квадратическое отклонение случайной величины, распределенной по нормальному закону, 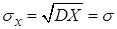 равно параметру
равно параметру 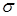 .
.
Общим называется нормальное распределение с произвольными параметрами 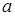 и
и 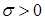 .
.
Нормированным называется нормальное распределение с параметрами 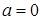 ,
, 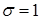 . Если
. Если 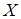 – нормальная случайная величина с параметрами
– нормальная случайная величина с параметрами 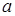 и
и 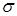 , то
, то 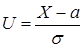 – нормированная нормальная случайная величина,
– нормированная нормальная случайная величина, 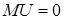 ,
, 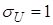 . Плотность нормированного распределения
. Плотность нормированного распределения 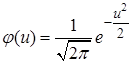 .
.
Функция общего нормального распределения
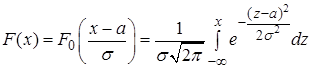 . (26)
. (26)
Вероятность попадания нормально распределенной случайной величины 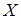 в интервал
в интервал 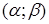
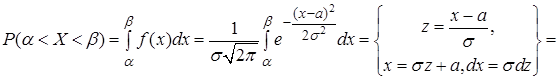
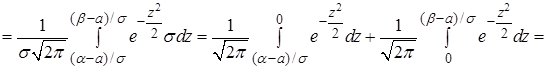
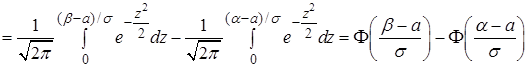 , (27)
, (27)
где 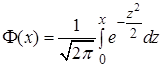 – функция Лапласа.
– функция Лапласа.
Найдем вероятность того, что отклонение нормально распределенной случайной величины 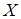 меньше заданного положительного числа
меньше заданного положительного числа 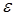 , используя формулу (27),
, используя формулу (27),
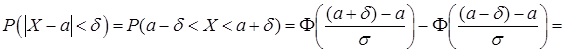
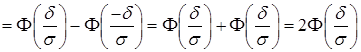 . (28)
. (28)
Показательный закон распределения. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины 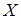 , которое описывается плотностью
, которое описывается плотностью
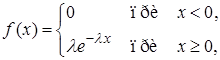 (29)
(29)
где 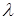 – постоянная положительная величина.
– постоянная положительная величина.
Показательное распределение определяется одним параметром 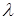 .
.
Функция распределения показательного закона
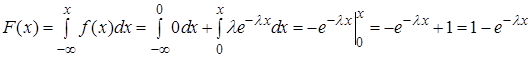 ,
,
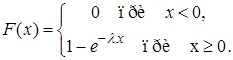 (30)
(30)
 |
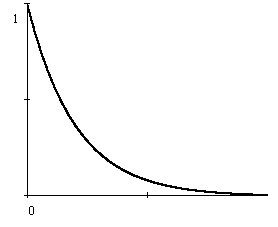
График плотности показательного распределения при 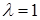

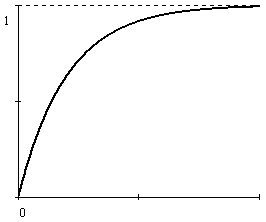
График функции показательного распределения при 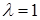
Вероятность попадания непрерывной случайной величины 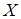 , распределенной по показательному закону, в интервал
, распределенной по показательному закону, в интервал 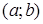
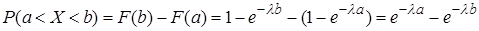 . (31)
. (31)
Найдем числовые характеристики случайной величины, распределенной по показательному закону. Математическое ожидание по формуле (12)
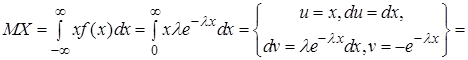
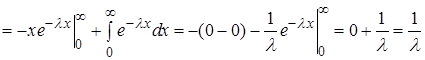 . (32)
. (32)
Дисперсия по формуле (16)
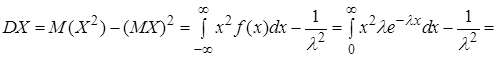
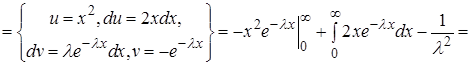
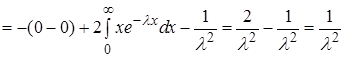 . (33)
. (33)
Среднее квадратическое отклонение 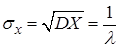 .
.
Рассмотрим одно из практических приложений показательного закона распределения.
Будем называть элементом некоторое устройство независимо от того, простое оно или сложное.
Пусть элемент начинает работать в момент времени 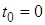 , а через время
, а через время 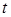 происходит отказ. Обозначим через
происходит отказ. Обозначим через 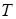 непрерывную случайную величину – длительность безотказной работы элемента. Если элемент проработал безотказно до наступления отказа время, меньшее
непрерывную случайную величину – длительность безотказной работы элемента. Если элемент проработал безотказно до наступления отказа время, меньшее 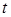 , то за время длительностью
, то за время длительностью 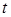 наступит отказ.
наступит отказ.
Функция распределения 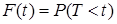 определяет вероятность отказа за время длительностью
определяет вероятность отказа за время длительностью 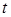 . Вероятность безотказной работы за то же время
. Вероятность безотказной работы за то же время 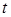
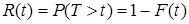 .
.
Функция 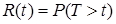 , определяющая вероятность безотказной работы элемента за время
, определяющая вероятность безотказной работы элемента за время 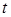 , называется функцией надежности.
, называется функцией надежности.
Если длительность безотказной работы элемента имеет показательное распределение, то функция 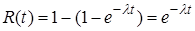 .
.
Показательным законом надежности называется функция надежности 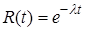 , где
, где 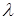 – интенсивность отказов.
– интенсивность отказов.
Этот закон обладает важным свойством: вероятность безотказной работы элемента на интервале времени длительностью 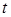 не зависит от продолжительности предыдущей работы до начала рассматриваемого интервала, а зависит только от длительности времени
не зависит от продолжительности предыдущей работы до начала рассматриваемого интервала, а зависит только от длительности времени 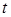 .
.
 2020-04-12
2020-04-12 597
597






