Дифференциальных уравнений

ЛЕКЦИЯ №6

РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ

Разработка и расчет новых изделий, аппаратов, конструкций или технологических процессов осуществляется на основе законов физики, механики, химии и т.д., которые обычно формулируются в виде дифференциальных уравнений. Математические модели многих, практически важных задач гидроаэромеханики, тепломассопереноса, теплопроводности, диффузии, теории упругости, задач на прочность, жесткость и устойчивость элементов конструкций и т.д. включают в свое описание дифференциальные уравнения в частных производных (их называют уравнениями математической физики). Решение большинства задач гидроаэромеханики, тепломассообмена, теории упругости и т.д. сводится к решению некоторых дифференциальных уравнений или системы дифференциальных уравнений. Например, расчет изгиба балки можно свести к решению краевой задачи для системы из двух обыкновенных дифференциальных уравнений второго порядка. Таким образом, любая задача проектирования, связанная с расчетом каких-либо конструкций, деталей, движения тел и т.д., в конечном счете, сводится к решению дифференциальных уравнений математических моделей. Для проведения вычислительного эксперимента на математической модели объекта исследования в силу ее сложности приходится использовать методы преобразования математической модели, например, методы линеаризации, дискретизации и т.д. Это существенно упрощает проведение вычислительного эксперимента на основе построенной математической модели.

Основные понятия, классификация, методы решения

дифференциальных уравнений

Дифференциальные уравнения в частных производных имеют бесконечное множество решений, т.к. их общее решение зависит от произвольных функций. При решении конкретной физической задачи необходимо из множества решений выбрать то, которое удовлетворяет некоторым дополнительным условиям. Такими дополнительными условиями чаще всего являются граничные условия (условия на границе заданной области) и начальные условия, относящиеся к моменту времени, с которого начинается исследуемый процесс. Совокупность граничных и начальных условий называется краевыми условиями. Нахождение решения дифференциального уравнения, удовлетворяющего начальным условиям (начальным данным), представляет собой задачу Коши. Задача нахождения решения дифференциального уравнения в некоторой области , удовлетворяющего на границе краевым условиям, является краевой задачей.

Для того чтобы решить математическую задачу (краевую задачу или задачу Коши) для каждого допустимого набора входных параметров, она должна быть корректно поставлена. Краевая задача называется корректно поставленной, если ее решение удовлетворяет следующим условиям: 1) решение существует; 2) решение единственно; 3) решение устойчиво, т.е. малым изменениям исходных данных соответствуют малые изменения решения (непрерывно зависит от исходных данных). Если хотя бы одно из этих условий не выполняется, то задача является некорректной. Для решения некорректно поставленных задач созданы специальные численные методы, получившие название методов регуляризации.

Для решения дифференциальных уравнений существуют аналитические и численные методы. Аналитические методы могут быть как точные (метод разделения переменных Фурье, метод функций Грина, и т.д.), так и приближенные (асимптотические, вариационные). Методы точного интегрирования дифференциальных уравнений позволяют найти решение в виде аналитической функции. Аналитические методы полезны не только тем, что дают возможность получать точные решения. Они имеют также огромное значение для построения численных методов. Например, проверка разностных схем на известных решениях простейших уравнений позволяет оценить эти схемы, выяснить их сильные и слабые стороны. Получение точного решения математической задачи – это одна из основных целей исследования.

Для большинства дифференциальных уравнений, встречающихся при решении практических задач, не удается получить точного решения в виде аналитической функции. В таких случаях используют численные методы, которые представляют решение дифференциального уравнения в виде таблицы значений искомой функции в некоторых узловых точках с определенной точностью (конечно-разностные методы, конечных элементов). Интенсивное развитие и внедрение в практику математического моделирования вычислительных машин с большим быстродействием (суперкомпьютеров) повысили роль численных методов при решении различных задач математической физики. Стало возможным проводить многовариантные расчеты математических моделей сложных физических явлений, проектирования сложных конструкций, исследования в различных областях науки и практики.

Выбор соответствующего метода для решения дифференциального уравнения зависит от его вида. Классификация дифференциальных уравнений с частными производными нужна еще потому, что для каждого класса уравнений существует своя общая теория и общие методы решения. Классификация выполняется на основе следующих основных признаков:

1) порядка дифференциального уравнения;

2) количества независимых переменных;

3) линейности уравнения;

4) однородности уравнения;

5) вида коэффициентов дифференциального уравнения;

6) типа дифференциального уравнения.

Классы уравнений в соответствии с указанными выше признаками представлены в таблице:

Признаки дифференциального уравнения	Классы дифференциальных уравнений
Порядок уравнения	Первого порядка		Старших порядков
Число переменных	Одна переменная Обыкновенное дифференциальное уравнение		Два и более переменных Уравнения в частных производных
Линейность уравнения	Линейные	Квазилинейные		Нелинейные
Однородность уравнения	Однородные		Неоднородные
Вид коэффициентов	С постоянными коэффициентами		С переменными коэффициентами
Тип уравнения	Эллиптического типа	Гиперболического типа		Параболического типа

Обыкновенные дифференциальные уравнения. Общий вид обыкновенного дифференциального уравнения, устанавливающего связь между независимой переменной 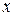, неизвестной функцией и ее производными , может быть представлен в виде:

. (7.1)

Порядок наивысшей производной, входящей в уравнение, называется порядком этого уравнения. Решением дифференциального уравнения является некоторая функциональная зависимость 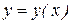, которая при подстановке в уравнение обращает его в тождество. Общее решение дифференциального уравнения, которое формально определяется интегрированием, записывается в виде , где – произвольные постоянные интегрирования.

Решение, полученное из общего решения при фиксированных значениях , называется частным решением уравнения. Постоянные интегрирования можно определить, если задать условий. Если эти условия задаются как совокупность значений искомой функции и всех ее производных до -го порядка включительно в некоторой точке , то такая задача называется задачей Коши, а заданные условия: , ,…, называются начальными условиями. Если же условия заданы на концах отрезка, где определяется решение, то задача называется краевой.

Дифференциальное уравнение (7.1) является линейным, если неизвестная функция и все ее производные входят в уравнение только в первой степени (и не перемножаются друг с другом), в противном случае уравнение является нелинейным. Общий вид обыкновенного линейного дифференциального уравнения -го порядка имеет вид:

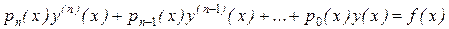, (7.2)

где – известные функции независимой переменной 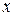, называемые коэффициентами уравнения. Функция в правой части называется свободным членом. Если все коэффициенты уравнения (7.2) являются постоянными, т.е. , то (7.2) является линейным дифференциальным уравнением с постоянными коэффициентами. Если уравнение (7.2) не содержит свободного члена, для всех значений независимой переменной, то оно является однородным дифференциальным уравнением. Для однородных дифференциальных уравнений выполняется принцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.

Простейшими дифференциальными уравнениями первого порядка, являются уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные и линейные уравнения первого порядка, которые можно решить интегрированием и получить точное решение. Нелинейные дифференциальные уравнения в общем случае не имеют разработанных аналитических методов решения, кроме некоторых частных классов. Для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения, без нахождения частного решения используется метод Лагранжа. В тех случаях, когда не удается получить точного решения обыкновенного дифференциального уравнения, применяются численные методы. Для численного решения задачи Коши можно использовать, например, методы Эйлера, Рунге-Кутта, Адамса и т.д. Для решения краевых задач часто применяют метод конечных разностей.

К числу важных обыкновенных дифференциальных уравнений, которые встречаются на практике, можно отнести: уравнение, описывающее второй закон Ньютона (классическая механика), уравнение Ван дер Поля (теория колебания), уравнение математического маятника, уравнения Бернулли, Риккати, Бесселя и т.д.

Дифференциальные уравнения в частных производных. Уравнение, связывающее искомую функцию , независимые переменные 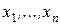и частные производные от искомой функции, называется дифференциальным уравнением в частных производных:

, (7.3)

где – заданная действительная функция точки некоторой области евклидова пространства 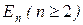и действительных аргументов. Порядок старшей частной производной, входящей в уравнение (3.3) называется порядком уравнения. Уравнение (7.3) называется квазилинейным, если функция линейна относительно старших производных, а коэффициенты уравнения при старших производных зависят только от переменной 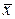. Уравнение (7.3) называется линейным, если функция линейна относительно функции и ее производных, а коэффициенты уравнения зависят только от переменной .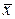

Многие практические задачи теплопроводности, диффузии, теории упругости и прочности и ряд задач из других областей описываются линейным дифференциальным уравнением в частных производных второго порядка, который можно записать в виде:

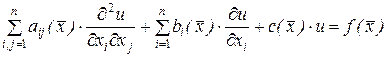, (7.4)

где – коэффициенты дифференциального уравнения, – свободный член. Все коэффициенты и свободный член дифференциального уравнения являются заданными функциями в области . Если для всех , то уравнение (7.4) называется однородным, в противном случае уравнение называется неоднородным. Если все коэффициенты уравнения являются постоянными, то уравнение (7.4) называется дифференциальным уравнением в частных производных с постоянными коэффициентами.

Для классификации дифференциальных уравнений в частных производных используют главную часть этих уравнений

с дифференциальным оператором , который после формальной замены на и на сводится к квадратичной форме следующего вида:

Матрица коэффициентов квадратичной формы является симметричной.

Для простоты рассмотрим уравнение с двумя независимыми переменными, т.е. , (). При фиксированном значении получаем уравнение

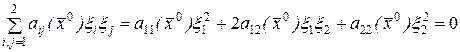. (7.5)

Это уравнение на плоскости описывает некоторую кривую второго порядка. Тип кривой определяется знаком определителя

Возможны три различных случая при фиксированном значении :

1) Определитель . В этом случае уравнение (7.5) является уравнением эллипса, а дифференциальное уравнение

(7.6)

называется уравнение эллиптического типа (в точке ).

2) Определитель . Тогда уравнение (7.5) описывает гиперболу, а уравнение (7.6) называется уравнением гиперболического типа (в точке ).

3) Определитель . В этом случае уравнение (7.5) будет уравнением параболы, а (7.6) – уравнением параболического типа (в точке ).

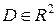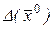Если уравнение (7.6) является эллиптическим, гиперболическим или параболическим в каждой точке области , то оно называется эллиптическим, гиперболическим или параболическим во всей области . Если Определитель меняет знак в области , то уравнение (7.6) – смешанного типа. Для классификации уравнений второго порядка при числе независимых переменных используется теория квадратичных форм. По каноническому виду квадратичной формы определяется тип дифференциального уравнения [44].

Рассмотрим несколько примеров:

1) Уравнение Пуассона (Лапласа) 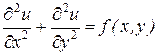– уравнение эллиптического типа ().

2) Уравнение теплопроводности (диффузии) – уравнение параболического типа ().

3) Волновое уравнение – уравнение гиперболического типа ().

Классические методы решения уравнений математической физики можно найти, например, в работе А. Н. Тихонова и А. А. Самарского [6]. Для решения уравнений математической физики обычно применяются методы разделения переменных, мгновенных источников, методы, основанные на применении функций Грина, Дирака и др. Эти классические методы предполагают отыскание, в первую очередь, общего решения и его последующее приспособление к частным условиям конкретной задачи. Также используются операционные методы, которые нашли применение в теплотехнике при решении разнообразных задач нестационарной теплопроводности, в химической технологии при решении задач нестационарной диффузии, при решении задач гидродинамики и др. Эффективными методами решения являются методы интегральных преобразований Лапласа, которые позволяют решать задачи без введения каких-либо новых допущений или преобразований, получать решения в форме, удобной для расчета.

При проведении вычислительного эксперимента математическая модель изучаемого объекта претерпевает ряд преобразований, необходимых для количественного анализа математической модели на вычислительной машине. Преобразования математической модели для количественного анализа непосредственно связаны с математическими методами. Для некоторых типов математических моделей без предварительных преобразований могут быть составлены алгоритмы численного решения, реализуемые на вычислительной машине. Например, математические модели в виде разностных уравнений, имитационные математические модели, являясь алгоритмическими математическими моделями, также не нуждаются в предварительном преобразовании перед реализацией на вычислительной машине. Часто имитационные математические модели используют в сочетании с методом статистических испытаний, методом Монте-Карло. Такой подход можно использовать и для решения дифференциальных уравнений с частными производными, если построить эквивалентную вспомогательную стохастическую математическую модель.

Краевой задаче, содержащей дифференциальные уравнения с частными производными и краевые условия, можно поставить в соответствие интегральную формулировку, т.е. можно представить в интегральной форме. При определенных условиях интегральную форму краевой задачи удается привести к вариационной формулировке минимизации некоторого функционала, который рассматривается на некотором множестве, содержащем искомую функцию. В этом случае говорят о вариационной форме модели. Для приближенного решения таких математических моделей, кроме приближенных аналитических вариационных методов Ритца, Бубнова-Галеркина, используется процедура метода конечных элементов (МКЭ), когда проводится дискретизация области конечными элементами и искомое решение приближенно представляется в виде линейной комбинации базисных функций. Для вычисления коэффициентов этой линейной комбинации необходимо решить систему линейных алгебраических уравнений относительно значений искомых функций в узлах конечных элементов.

Математические модели, содержащие в своем описании дифференциальные уравнения, могут быть достаточно сложными, нелинейными, в этом случае особое значение имеют методы линеаризации. Например, нелинейные модели разлагаются в ряд Тейлора и в первом приближении получаются линейные модели, а они достаточно хорошо изучены. Чтобы сделать возможным численное решение дифференциальных уравнений строится дискретная модель математической задачи, дифференциальные уравнения заменяются дискретными алгебраическими аппроксимациями и в результате этого получаются алгебраические системы уравнений. Наиболее удобными математическими моделями с точки зрения реализации на вычислительной машине являются линейные математические модели в виде системы линейных алгебраических уравнений. Поэтому многие математические методы, связанные с преобразованием математических моделей, ориентированы на последовательное сведение исходной математической модели к модели в виде системы линейных алгебраических уравнений.

Конечно-разностные методы решения краевых задач

Без применения ЭВМ лишь немногие краевые задачи математической физики в силу их сложности удается решить аналитически. Поэтому численные методы решения задач математической физики играют очень важную роль в практике инженерных расчетов.

При численных методах решения дифференциальных уравнений искомое решение получается в виде таблицы числовых значений в некотором заданном наборе значений аргументов (в узловых точках сетки). Исходное дифференциальное уравнение заменяется некоторым конечно-разностным аналогом, т.е. присутствующие в уравнении и в краевых условиях производные аппроксимируются (заменяются) конечными разностями в узлах сетки. В итоге, после постановки их вместо производных в исходную краевую задачу, решение краевой задачи сводится к решению системы уравнений относительно значений искомой функции в узловых точках. Причем, численными методами удается получить только частное решение дифференциального уравнения. Набор разностных уравнений, определенных на некоторой сетке, называется конечно-разностной схемой (или просто разностной схемой). Схему построения численного решения дифференциальных уравнений в частных производных методом конечных разностей можно представить в виде:

Процесс построения численного решения дифференциального уравнения можно представить в следующем виде:

Численное решение дифференциальных уравнений математической физики методом конечных разностей проводится в два этапа: 1) разностная аппроксимация дифференциального уравнения на выбранной сетке – построение разностной схемы (дискретизация); 2) решение на ЭВМ разностных уравнений, представляющих собой систему линейных или нелинейных разностных уравнений большой размерности специального вида (плохая обусловленность, ленточная структура и т.д.). Причем, если исходное дифференциальное уравнение является нелинейным, то конечно-разностная аппроксимация приводит к системе нелинейных уравнений.

Рассмотрим конечно-разностную аппроксимацию производных и оценки погрешности полученных формул (точность аппроксимаций) для функции одной переменной. Для получения формул, аппроксимирующих производные, рассмотрим разложение непрерывной функции в ряд Тейлора в окрестности точки :

(7.7)

При малых значениях , отбросив малые члены более высоких порядков относительно (пренебрегая ими) в разложении (7.7), можно получить выражения для аппроксимации производных. Погрешность аппроксимации определяетс я старшим членом в отброшенном остатке, который содержит , где определяет порядок точности аппроксимации. Для обозначения остаточного члена разложения используется специальная символика – «о малое от », которая определяется как «бесконечно малое относительно », т.е. , . Для обозначения остаточного члена разложения также используется символика – «О большое от », т.е. .

Для аппроксимации производных первого порядка в разложении (7.7) можно оставить два первых члена, т.е. линейную часть относительно :

Тогда конечно-разностные аналоги для аппроксимации производных первого порядка можно записать в виде:

, (7.8)

. (7.9)

Выражение (7.8) используется для аппроксимации правой производной, взятой с шагом вперед, выражение (7.9) – для левой производной, взятой с шагом назад. Определим порядок точности конечно-разностной аппроксимации производных первого порядка по формулам (7.8) и (7.9). Погрешность такой аппроксимации определяется старшим членом в отброшенном остатке. Заменяя в (7.8) значение разложением в ряд Тейлора (7.7), получим:

Таким образом, формула (7.8) имеет аппроксимацию первого порядка. Определим погрешность аппроксимации для левой производной по формуле (7.9):

Формула (7.9) для аппроксимации левой производной имеет первый порядок точности.

Для аппроксимации производных первого порядка также можно построить конечно-разностные аналоги более высокого порядка. Для этого разложение (7.7) запишем в виде:

(7.10)

(7.11)

Далее, если из разложения (7.10) почленно вычесть разложение (7.11), то из разложения разности исчезнут свободный член и члены четных степеней относительно :

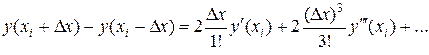
Если в последнем разложении разности оставить линейную часть относительно , то можно получить более точную аппроксимацию первой производной, которая называется центральной разностью:

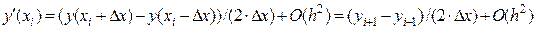. (7.12)

В этом случае остаточный член в отброшенном остатке, определяющий погрешность аппроксимации, будет содержать во второй степени. Таким образом, формула (7.12) имеет второй порядок точности.

Чтобы построить конечно-разностные аналоги для аппроксимации производных второго порядка, следует сложить разложение (7.10) почленно с разложением (7.11). Тогда из разложения суммы исчезнут члены нечетных степеней относительно :

Если в последнем разложении суммы оставить члены до второго порядка включительно относительно , то получим формулу для аппроксимации производной второго порядка ():

.(7.13)

Отброшенный остаток будет содержать член с во второй степени (после деления на ), т.е. формула (7.13) для аппроксимации второй производной имеет второй порядок точности.

Основываясь на выражениях для 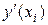, и на формальные правила дифференцирования, можно получить аппроксимации производных третьего, четвертого и более старших порядков.

Например:

, (7.14)

. (7.15)

Это общий подход, который позволяет конструировать аппроксимации производных разностными выражениями так, что ошибка, возникающая при такой замене, будет иметь любой заданный порядок относительно шага сетки для достаточно гладкой функции (гладкость функции – непрерывность ее первых производных). Существуют и другие процедуры построения разностных отношений, например, метод неопределенных коэффициентов. В этом случае общая формула для аппроксимации производных в некоторой точке имеет следующий вид:

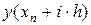где коэффициенты подбираются таким образом, чтобы добиться требуемого порядка аппроксимации. Пределы суммирования и подчиняются условию . Заменяя в уравнении разложением ряда Тейлора в виде

получим следующее разложение:

. Приравнивая коэффициенты при , в левой и правой частях этого выражения, мы придем к системе уравнений для определения 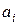: , , …, , , , …, . Если , то мы имеем систему из линейных уравнений для неизвестных . Определитель матрицы коэффициентов этой системы есть определитель Вандермонда, который не равен нулю. Таким образом, в этом случае существует единственный набор коэффициентов , удовлетворяющих системе уравнений. Если , то решение системы относительно коэффициентов 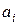не единственно.

Рассмотрим применение метода конечных разностей на примере решения краевой задачи для линейного обыкновенного дифференциального уравнения второго порядка:

(I)

(II)

(III)

где , функции являются непрерывными на заданном отрезке .

Решение краевой задачи заключается в определении значения функции , удовлетворяющего уравнению (I) и краевым условиям (II)-(III). Основная идея численного решения краевой задачи (I)-(III) методом конечных разностей (МКР) заключается в следующем: в заданной области выбирается система узловых точек и задача считается решенной, если найдены значения искомой функции в узловых точках. При этом решение проводится в два этапа: 1) конечно-разностная аппроксимация производных дифференциального уравнения и краевых условий, т.е. составление конечно-разностного аналога задачи (дискретизация) – получается система уравнений; 2) решение полученной системы уравнений относительно значений искомой функции в узлах сетки.

На заданном отрезке выбирается сетка узлов: .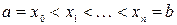

Для удобства расчетов можно выбрать и равномерную сетку: . Далее, дифференциальное уравнение (I)

рассматривается во внутренних узлах , где :

Заменяя первые и вторые производные во внутренних узлах центральными конечно-разностными аналогами (7.12) и (7.13), получим систему из -го уравнения с -им неизвестным относительно :

где .

Недостающие два уравнения получим из аппроксимации краевых условий (II) и (III). Производные первого порядка в краевых условиях заменяются конечно-разностными аналогами (7.8) и (7.9):

В итоге получим недостающие два уравнения:

и .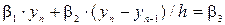

Таким образом, для определения -го неизвестного получили систему из -го линейного алгебраического уравнения:

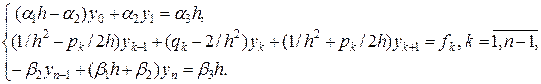(IV)

Несмотря на то, что во внутренних узлах разностные формулы приближают дифференциальное уравнение (I) со вторым порядком аппроксимации, решение получается только с первым порядком из-за понижения порядка аппроксимации краевых условий (II) и (III) в граничных точках. При аппроксимации граничных условий второго и третьего рода (условия на производные и смешанные условия) конечно-разностными аналогами первого порядка в итоге решение краевой задачи получается только с первым порядком аппроксимации. Но все же желательно, чтобы разностная схема имела второй порядок аппроксимации во всех точках, включая и граничные. Существует несколько способов повышения порядка аппроксимации в граничных точках:

1. Использование формул одностороннего дифференцирования более высокого порядка точности.

2. Расширение сеточной области добавлением фиктивного узла.

3. Использование разложения искомой функции в ряд Тейлора в граничных точках.

В качестве примера рассмотрим метод расширения сеточной области добавлением слева и справа по одному узлу, которые находятся за пределами заданного отрезка . Пусть в этих точках также определенны значения сеточной функции: и .

Далее дифференциальное уравнение (I) и краевые условия (II) и (III) аппроксимируем в граничных точках и со вторым порядком. Замена первых и вторых производных дифференциального уравнения (I) в граничных точках и центральными конечно-разностными аналогами второго порядка (7.12) и (7.13) приводит к линейным уравнениям:

, (A)

. (B)

Аппроксимация краевых условий (II) и (III) центральной разностью второго порядка (7.12) в граничных точках и дает уравнения:

(С)

. (D)

Следующим шагом из уравнения (С) исключается значение сеточной функции в фиктивной точке , а из уравнения (D) – значение сеточной функции в фиктивной точке . Для этого из уравнения (A) выражается значение и подставляется это значение в уравнение (С). Аналогично, из уравнения (B) выражается значение и подставляется в уравнение (D). Теперь остается только первое и последнее уравнения системы (IV) заменить новыми уравнениями (С) и (D). В итоге построена разностная схема, которая имеет второй порядок аппроксимации во всех узловых точках сеточной области, включая и граничные.

Для решения полученной системы можно использовать, например, метод Гаусса. Матрица полученной системы является трех диагональной, поэтому для ее решения часто применяют метод прогонки.

Аналогичным образом, как и для функции одной переменной, используя разложение в ряд Тейлора функции многих переменных, можно получить конечно-разностные аппроксимации частных производных. Например, для функции двух переменных выражения для конечных разностей в предположении, что первый индекс относится к координате , а второй – , т.е. и принимая , , будут представлены в виде:

– центральная разность по оси ,

– вторая разность по оси 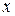, (7.16)

– вторая разность по оси ,

– смешанная разность второго порядка по осям и . В выражениях (7.16) отброшены члены порядка или . Эти формулы являются центрально-разностными аппроксимациями второго порядка. Также возможны другие аппроксимации, более точные.

Конфигурацию узлов, используемую для составления разностной схемы (разностных алгебраических уравнений), называют шаблоном. Для решения одной и той же задачи можно использовать разные шаблоны. На рис.7.1 приводятся некоторые варианты вычислительных шаблонов для конечно-разностной аппроксимации частных производных функции двух переменных:

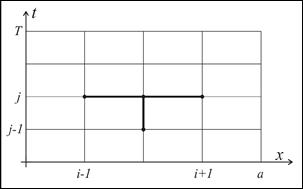Рис. 7.1

Конечно-разностные аппроксимации являются некоторыми приближениями значений производных, имеют разную точность аппроксимации. Существует три источника погрешностей, связанных с численной аппроксимацией:

1) Погрешность округления обусловлена ограничениями на представление чисел в используемой ЭВМ, т.к. дробные числа в двоичной системе счисления представляются в виде бесконечной последовательности двоичных знаков (0 и 1), а число значащих цифр ограничено.

2) Погрешность усечения (дискретизации) связана с тем, что для аппроксимации функции вместо бесконечных рядов используется лишь несколько первичных членов (не зависит от ЭВМ).

3) Погрешность распространения является результатом накопления погрешностей, появившихся на предыдущих этапах счета.

Указанные три источника погрешностей являются причиной наблюдаемых ошибок двух типов:

1) Локальная ошибка – сумма погрешностей, вносимых в вычислительный процесс на каждом шаге вычислений, т.е. разность между вычисленным решением и теоретическим решением, определяемыми одними и теми же данными в некоторой фиксированной точке.

2) Глобальная ошибка – разность между вычисленным и точным решением, определяющая суммарную погрешность численного алгоритма, накопившуюся с момента начала вычислений.

Фундаментальным понятием при оценке точности численного метода является его порядок, который определяется в терминах локальной ошибки, получаемой при применении метода к задачам с гладким решением. Говорят, что численный метод имеет порядок , если существует число , такое, что для локальной ошибки выполняется условие , где – абсолютная величина локальной ошибки между теоретическим решением и приближенным решением, полученным с помощью численного метода на -м шаге, – не зависит от номера шага и величины шага , т.е. имеет место выражение . Расчетная формула численного метода согласуется (совпадает) с разложением решения в ряд Тейлора до членов порядка , тогда – порядок метода. Таким образом, порядок точности численного метода определяется порядком зависимости ошибки от величины шага. Например, метод Эйлера для решения обыкновенных дифференциальных уравнений (ОДУ) имеет первый порядок точности, так как для него зависимость ошибки от величины шага линейна, т.е. при уменьшении шага в 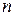раз ошибка также уменьшается в раз. Расчетная формула метода Рунге-Кутты для решения ОДУ содержит первые члены ряда Тейлора до четвертого порядка включительно относительно шага. Следовательно, он имеет четвертый порядок точности.

Следует отметить, если локальная ошибка есть , то глобальная ошибка будет . Также, определение порядка точности численного метода согласуется с определением погрешности аппроксимации производных конечно-разностными аналогами, которая определяется старшим членом в отброшенном остатке разложения в ряд Тейлора. Существует и другие подходы к определению понятия алгебраического порядка точности численного метода. Например, порядком точности численного метода называется наибольшая степень алгебраического полинома, для которой численный метод дает точное решение.