Задания для практической работы

МАТЕМАТИКА

Группа 87

Машинист крана (крановщик)

Марта 2020 г.

Практическое занятие

 

Тема: «Равносильность равнений»

 

Цели:

- обобщить и систематизировать знания учащихся уравнений с одной переменной;

- развитие мышления учащихся; развитие познавательного интереса и умений учебно-познавательной деятельности;

- воспитание организованности, самоконтроля и взаимоконтроля.

 

Продолжительность занятия  - 2 часа

 

Оборудование:  карточки с заданиями, чертежные инструменты, ручка, тетрадь

Краткие теоретические сведения:

Краткое обсуждение  тех теоретических знаний, которыми они обладают и пользуются при решении уравнений.

Допустим, нам необходимо решить уравнение

3-(2х- 5) = 2х + 5.

Преобразуем данное уравнение, выстраивая цепочку уравнений и стараясь получить уравнение вида а х = b, т.е. линейное уравнение

6х - 15 = 2х + 5,        6х - 2х = 5 + 15,      4х = 20.

Откуда получаем, что 5 - корень уравнения. Причём, как последнего уравнения, так и любого из уравнений данной цепочки, так как они являются равносильными уравнениями. По сути, решением уравнения и является выстраивание подобных цепочек уравнений.

1)   Определение. Два уравнения с одной переменной f(х) = g(х) и h(х) = р(х) называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

Например, уравнения 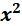 - 4 = 0 и (х + 2)(2^Х - 4) = 0 равносильны; равносильны и уравнения х² + 1 = 0 и 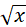= - 2 - они не имеют корней.

2)   Определение. Если каждый корень уравнения    f(х) = g(х) (1)

является в то же время корнем уравнения   h(х) = р(х) (2),

то уравнение (2) называется следствием уравнения (1).

Например, уравнение х - 2 = 3 имеет корень 5, уравнение 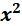 - 25 = 0 имеет корни ± 5. Так как корень уравнения х - 2 = 3 является корнем уравнения х² - 25 = 0, то уравнение х² - 25 = 0 является следствием,, уравнения х - 2 = 3.

Следовательно, два уравнения называют равносильными тогда и только тогда, когда каждое из них является следствием другого.

3)   Если в ходе преобразований, при переходе от одного из уравнений к уравнению-следствию, мы неуверенны в равносильности выполняемогоперехода, то у последнего уравнения могут появиться посторонние корни в отношении исходного уравнения. Поэтому все полученные корни уравнения- следствия необходимо проверить, подставляя их в исходное уравнение. Тем самым, проверка найденных корней уравнения является не проверкой верности выполненных технических преобразований, а неотъемлемой частью, этапом решения уравнения.

4) Итак, мы выяснили, что в процессе решения уравнений (а ещё более при решении неравенств) на каждом этапе преобразований крайне важно знать, равносильный ли переход мы совершаем. Сформулируем и обсудим ряд важных для нас положений.

Теорема 1. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному уравнению.

Теорема 2. Если обе части уравнения возвести в одну и ту же нечётную степень, то получится уравнение, равносильное данному уравнению.

Теорема 3. Показательное уравнение (где > 1, 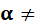 1) равносильно уравнению f(х) = g(х).

Определение. Областью определения уравнения f(х) = g(х) или ОДЗ переменной уравнения называется множество тех значений х, при которых одновременно имеют смысл обе части уравнения f(х) = g(х).

Теорема 4. Если обе части уравнения f(х) = g(х) умножить на одно и то же выражение h(х), которое имеет смысл всюду в области определения (ОДЗ) уравнения f(х) = g(х) и при этом нигде в этой области h(х)  0, то уравнения f(х) = g(х) и h(х)∙f(х) =h(х) g(х) равносильны.

То есть, мы можем обе части уравнения умножать или делить на одно и то же отличное от нуля число, не нарушая при этом равносильности уравнений.

Теорема 5. Если обе части уравнения f(х) = g(х) неотрицательны на ОДЗ уравнения, то после возведения обеих его частей в одну и ту же степень n получится уравнение gⁿ(x), равносильное исходному уравнению.

Теорема 6. Если f(х)>0, = g(х)>0, то уравнение log_α2 f(x) = log_α g(x), где а>0, 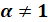, равносильно уравнению f(х) = g(х).

6) Выводы. Исходное уравнение преобразуется в процессе решения в уравнение-следствие, значит, необходимо обязательное выполнение проверки всех найденных корней, если: расширилась ОДЗ уравнения; возводились в одну и ту же чётную степень обе части уравнения; выполнялось умножение обеих частей уравнения на одно и тоже выражение с переменной.

Пусть на дано уравнение 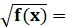g(x) Возведя в квадрат обе части уравнения, получим уравнение f(х) = g²(х) которое можно записать так:

( -g(x)) ( +g(x))=0

Откуда получаем совокупность уравнений: .

Имеем постороннее уравнение, и могут появиться посторонние корни. Следовательно, необходима проверка корней. Если мы захотим выполнить равносильный переход и обойтись без проверки, то исходное уравнение

равносильно смешанной системе:

5) Выводы. При решении иррациональных уравнений - возведении обеих частей уравнения в чётную степень, принадлежность полученных корней ОДЗ уравнения не позволяет сделать вывод, о том являются ли эти корни посторонними или нет. Поэтому выполнение проверки корней обязательно и это этап решения уравнения. Если корень не принадлежит ОДЗ то он, конечно, посторонний корень уравнения. В то же время, записывая систему равносильную уравнению, мы не нарушаем логики решения уравнения: ведь уравнение с пустой ОДЗ равносильно системе, не имеющей решений.

 

Задания для практической работы

Вариант 1   

1. Найти функцию, обратную к данной:

а) у = – 3х + 2; б) у = 2 – х³; в) у = .

2. Выяснить равносильны ли уравнения:

2х² - 9х – 5 = 0 и х(6х – 13) = 14х +15

3. Решить уравнения:

а) ; б) );

4. Решить уравнение:

Вариант 2

1. Найти функцию, обратную к данной:

а) у = 2х – 3; б) у = х² – 3; в) у =

2. Выяснить равносильны ли уравнения:

5 х² + 4х – 1 = 0 и х(2х +11) = - 6 - х²

3.Решить уравнения:

а) s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> ; б) .

 

4. Решить уравнение:

 

 

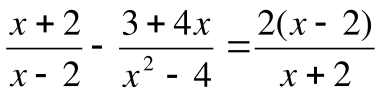
Домашнее задание:

Оформить отчет по практической работе

Список литературы:

Алгебра и начала математического анализа, автор Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева, учебник для общеобразовательных организаций, базовый и углубленный уровни, 5 издание, Москва «Просвещение», 2019г.