Скалярне поле
Нехай  – область у тривимірному просторі (або на площині). Кажуть, що в області
– область у тривимірному просторі (або на площині). Кажуть, що в області  задано скалярне поле, якщо кожній точці
задано скалярне поле, якщо кожній точці  поставлено у відповідність деяке число
поставлено у відповідність деяке число 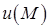 .
.
Прикладами скалярних полів є поле температури даного тіла, поле густини даного неоднорідного середовища, поле вологості повітря, поле атмосферного тиску, поле потенціалів заданого електростатичного поля тощо.
Поверхня (лінія), на якій функція 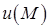 набуває одне й те саме значення, називається поверхнею (лінією) рівня скалярного поля (наприклад, поверхні або лінії постійної температури). Надаючи
набуває одне й те саме значення, називається поверхнею (лінією) рівня скалярного поля (наприклад, поверхні або лінії постійної температури). Надаючи 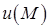 різних постійних значень:
різних постійних значень:  , отримаємо сім’ю поверхонь (ліній) рівня даного скалярного поля.
, отримаємо сім’ю поверхонь (ліній) рівня даного скалярного поля.
Фізичні скалярні поля не залежать від вибору системи координат: величина  є функцією лише точки
є функцією лише точки  і, можливо, часу (нестаціонарні поля).
і, можливо, часу (нестаціонарні поля).
Якщо в просторі ввести прямокутну систему координат  , то точка
, то точка  у цій системі координат матиме певні координати
у цій системі координат матиме певні координати  і скалярне поле
і скалярне поле  стане функцією цих координат:
стане функцією цих координат: 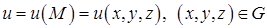 .
.
Векторне поле
Кажуть, що в області  задано векторне поле, якщо кожній точці
задано векторне поле, якщо кожній точці  поставлено у відповідність деякий вектор
поставлено у відповідність деякий вектор  .
.
Фізичні приклади векторних полів: електричне поле системи електричних зарядів, яке характеризується в кожній точці вектором напруженості  ; магнітне поле, утворене електричним струмом і яке характеризується в кожній точці вектором магнітної індукції
; магнітне поле, утворене електричним струмом і яке характеризується в кожній точці вектором магнітної індукції  ; поле тяжіння, утворене системою мас і яке характеризується в кожній точці вектором сили тяжіння
; поле тяжіння, утворене системою мас і яке характеризується в кожній точці вектором сили тяжіння  , що діє в цій точці на одиничну масу; поле швидкостей потоку рідини, яке описується в кожній точці вектором швидкості
, що діє в цій точці на одиничну масу; поле швидкостей потоку рідини, яке описується в кожній точці вектором швидкості  .
.
Зручною геометричною характеристикою векторного поля  є векторні лінії – криві, в кожній точці
є векторні лінії – криві, в кожній точці  яких вектор
яких вектор  напрямлений по дотичній до кривої. Векторні лінії поля тяжіння, електричного і магнітного полів називається силовими лініями, а поля швидкостей – лініями струму.
напрямлений по дотичній до кривої. Векторні лінії поля тяжіння, електричного і магнітного полів називається силовими лініями, а поля швидкостей – лініями струму.
Нехай векторна лінія, яка проходить через точку  , описується рівнянням
, описується рівнянням  , де
, де  – параметр. Умова колінеарності вектора поля
– параметр. Умова колінеарності вектора поля  і дотичного вектора
і дотичного вектора  в довільній точці цієї лінії має вигляд
в довільній точці цієї лінії має вигляд
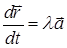 ,(1)
,(1)
де  – деяке число. Умову (1) можна записати також у вигляді
– деяке число. Умову (1) можна записати також у вигляді
 (2)
(2)
або, помноживши на  , у вигляді
, у вигляді
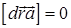 .(3)
.(3)
Кожне із рівнянь (1) – (3) є диференціальним рівнянням векторних ліній у векторній формі і визначає множину векторних ліній. Конкретна векторна лінія, яка проходить через задану точку  , визначається додатковою умовою
, визначається додатковою умовою
 ,(4)
,(4)
де 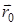 – радіус-вектор точки
– радіус-вектор точки  .
.
Фізичні векторні поля не залежать від системи координат: в кожній точці  вектор
вектор  повністю визначається своїм модулем
повністю визначається своїм модулем 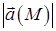 і напрямом. Якщо в просторі введена прямокутна система координат
і напрямом. Якщо в просторі введена прямокутна система координат  , то векторне поле
, то векторне поле  описується вектор-функцією трьох змінних
описується вектор-функцією трьох змінних  або трьома скалярними функціями – її координатами:
або трьома скалярними функціями – її координатами:
 .
.
Оскільки в прямокутних координатах 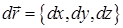 , то векторне рівняння (3) для векторних ліній еквівалентне системі диференціальних рівнянь
, то векторне рівняння (3) для векторних ліній еквівалентне системі диференціальних рівнянь
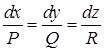 ,(5)
,(5)
а додаткове векторне рівняння (4) еквівалентне таким умовам:
 ,(6)
,(6)
де 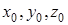 – координати точки
– координати точки  .
.
Похідна за напрямом
Скалярне і векторне поля
 і
і 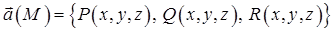
Називаються диференційованими 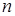 разів, якщо функції
разів, якщо функції

диференційовані 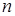 разів. Надалі розглядатимемо поля, диференційовані потрібне нам число разів.
разів. Надалі розглядатимемо поля, диференційовані потрібне нам число разів.
Нехай 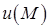 – скалярне поле, задане в області
– скалярне поле, задане в області  ,
,  – одиничний фіксований вектор;
– одиничний фіксований вектор;  – фіксована точка;
– фіксована точка; 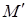 – довільна точка із
– довільна точка із  , відмінна від
, відмінна від  і така, що вектор
і така, що вектор  колінеарний
колінеарний  . Нехай, далі,
. Нехай, далі,  – величина напрямленого відрізка
– величина напрямленого відрізка  (вона дорівнює його довжині
(вона дорівнює його довжині 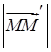 , якщо напрям вектора
, якщо напрям вектора  збігається з напрямом вектора
збігається з напрямом вектора 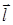 , і дорівнює –
, і дорівнює – 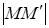 , якщо вектори
, якщо вектори  і
і 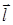 є протилежними).
є протилежними).
Означення. Число  називається похідною скалярного поля
називається похідною скалярного поля 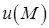 (функції
(функції 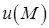 ) в точці
) в точці  за напрямом
за напрямом 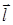 і позначається символом
і позначається символом  .
.
Похідна за напрямом  є швидкістю зміни функції
є швидкістю зміни функції 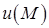 за напрямом
за напрямом 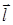 в точці
в точці  .
.
Якщо в прямокутній системі координат 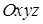
 , то
, то
 .(7)
.(7)
Зокрема, якщо вектор 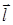 збігається з одним із ортів
збігається з одним із ортів 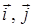 або
або  , то похідна за напрямком
, то похідна за напрямком 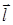 збігається з відповідною частинною похідною. Наприклад, якщо
збігається з відповідною частинною похідною. Наприклад, якщо 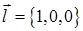 , то
, то
 .
.
Аналогічно визначається похідна за напрямом векторного поля.
Означення. Вектор  називається похідною векторного поля
називається похідною векторного поля  (вектор-функції
(вектор-функції  ) в точці
) в точці  за напрямом
за напрямом 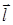 і позначається символом
і позначається символом 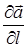 .
.
Якщо в прямокутній системі координат 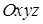
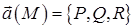 , то
, то
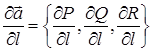 .
.
Градієнт скалярного поля
скалярне векторне поле дивергенція
Означення. Градієнтом скалярного поля  називається вектор-функція
називається вектор-функція
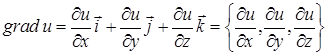 .
.
Із рівності (7) випливає, що
 ,(8)
,(8)
Звідси  , оскільки
, оскільки 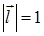 .
.
Тут  – кут між векторами
– кут між векторами 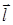 і
і  в точці
в точці  . Очевидно, що
. Очевидно, що 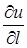 має найбільше значення при
має найбільше значення при 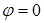 , тобто у напрямі
, тобто у напрямі  в даній точці. Інакше кажучи, вектор
в даній точці. Інакше кажучи, вектор  в даній точці вказує напрям найбільшого зростання поля
в даній точці вказує напрям найбільшого зростання поля 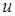 (функції
(функції 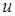 ) у цій точці, а
) у цій точці, а  є швидкість зростання функції
є швидкість зростання функції 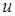 в цьому напрямі. Таким чином, вектор
в цьому напрямі. Таким чином, вектор  не залежить від вибору системи координат, а його модуль і напрям у кожній точці визначається самою функцією
не залежить від вибору системи координат, а його модуль і напрям у кожній точці визначається самою функцією 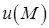 .
.
Потенціальне поле
Означення. Векторне поле 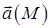 називається потенціальним в області
називається потенціальним в області 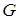 , якщо воно збігається в області
, якщо воно збігається в області 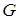 з полем градієнта деякого скалярного поля
з полем градієнта деякого скалярного поля 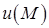 :
:
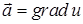 .(9)
.(9)
Функція  називається скалярним потенціалом векторного поля
називається скалярним потенціалом векторного поля  . Якщо
. Якщо 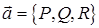 , то із рівності (9) випливає, що
, то із рівності (9) випливає, що
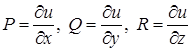 .
.
Інколи потенціалом векторного поля  називають таку функцію
називають таку функцію 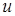 , що
, що  .
.
Розглянемо, наприклад, поле тяжіння точкової маси  , розміщеної на початку координат. Воно описується вектор-функцією
, розміщеної на початку координат. Воно описується вектор-функцією  (
(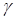 – гравітаційна стала,
– гравітаційна стала,  ). З такою силою діє це поле на одиничну масу, розміщену в точці
). З такою силою діє це поле на одиничну масу, розміщену в точці 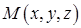 . Поле тяжіння є потенціальним. Його можна подати у вигляді градієнта скалярної функції
. Поле тяжіння є потенціальним. Його можна подати у вигляді градієнта скалярної функції 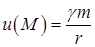 , яка називається ньютонівським потенціалом поля тяжіння точкової маси
, яка називається ньютонівським потенціалом поля тяжіння точкової маси 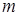 . Дійсно
. Дійсно
 .
.
Аналогічно  , звідси
, звідси
 .
.
Далі, розглянемо ще один приклад. Нехай задано електричне поле точкового заряду 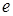 , розміщеного на початку координат. Воно описується в точці
, розміщеного на початку координат. Воно описується в точці  вектором напруженості
вектором напруженості
 .
.
Це поле також є потенціальним полем. Його можна подати у вигляді 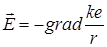 . Функція
. Функція  називається потенціалом електричного поля точкового заряду
називається потенціалом електричного поля точкового заряду 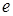 .
.
Поверхні рівня потенціала 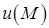 називаються еквіпотенціальними поверхнями.
називаються еквіпотенціальними поверхнями.
Дивергенція
Означення. Дивергенцією векторного поля  називається скалярна функція
називається скалярна функція
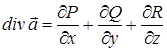 .
.
Слово «дивергенція» означає «розбіжність».
Дивергенція характеризує густину джерел даного векторного поля в розглянутій точці.
Розглянемо, наприклад, електричне поле точкового заряду 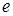 , розміщеного в початку координат:
, розміщеного в початку координат:
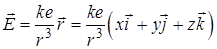 ,
,
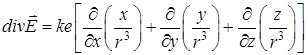 .
.
Оскільки  , і аналогічно
, і аналогічно  , то
, то 
(при 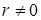 ). Цей результат означає відсутність поля у довільній точці, крім початку координат. В початку координат
). Цей результат означає відсутність поля у довільній точці, крім початку координат. В початку координат  .
.
Ротор
Означення. Ротором (або вихором) векторного поля
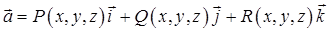
називається вектор-функція
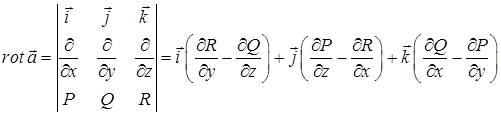 .
.
Зокрема, для плоского поля  маємо
маємо
 .
.
Розглянемо тверде тіло, яке обертається навколо осі  із сталою кутовою швидкістю
із сталою кутовою швидкістю  (рис. 1).
(рис. 1).
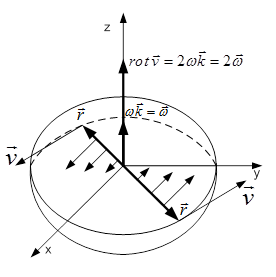
Рисунок 1 – Тверде тіло, яке обертається навколо осі 
Векторне поле швидкостей  точок цього тіла можна подати у вигляді
точок цього тіла можна подати у вигляді
 .
.
Знайдемо ротор поля швидкостей 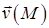 :
:
 .
.
Таким чином,  є сталим вектором, напрямленим уздовж осі обертання
є сталим вектором, напрямленим уздовж осі обертання 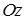 , а його модуль дорівнює подвоєній кутовій швидкості обертання тіла:
, а його модуль дорівнює подвоєній кутовій швидкості обертання тіла:
 .
.
Розглянемо потенціальне поле  . Його потенціал
. Його потенціал  . Обчислимо ротор цього поля:
. Обчислимо ротор цього поля:
 .
.
Взагалі, ротор довільного потенціального поля дорівнює нулю (див. підрозділ 2). Тому кажуть, що потенціальне поле є безвихровим.
Соленоїдальне поле
Векторне поле  називається соленоїдальним в області
називається соленоїдальним в області  , якщо в цій області
, якщо в цій області  . Оскільки
. Оскільки 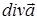 характеризує густину джерел поля
характеризує густину джерел поля  , то в тій області, де поле соленоїдальне, немає джерел цього поля.
, то в тій області, де поле соленоїдальне, немає джерел цього поля.
Наприклад, електричне поле 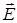 точкового заряду соленоїдальне (задовольняє умову
точкового заряду соленоїдальне (задовольняє умову  ) всюди поза точкою, де знаходиться заряд (в цій точці
) всюди поза точкою, де знаходиться заряд (в цій точці  ). Векторні лінії соленоїдального поля не можуть починатися або закінчуватися на межі області, або бути замкненими кривими. Прикладом соленоїдального поля з замкненими векторними лініями є магнітне поле, яке створюється струмом у провіднику.
). Векторні лінії соленоїдального поля не можуть починатися або закінчуватися на межі області, або бути замкненими кривими. Прикладом соленоїдального поля з замкненими векторними лініями є магнітне поле, яке створюється струмом у провіднику.
Якщо векторне поле  можна подати як ротор деякого векторного поля
можна подати як ротор деякого векторного поля 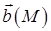 , тобто
, тобто  , то вектор – функція
, то вектор – функція 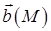 називається векторним потенціалом поля
називається векторним потенціалом поля  .
.
Можна перевірити (див. докладніше п. 2), що 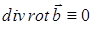 , тобто поле
, тобто поле 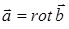 є соленоїдальним.
є соленоїдальним.
Довільне векторне поле можна подати у вигляді суми потенціального і соленоїдального полів.
Оператор Гамільтона
Згадаємо, що символ  називається оператором частинної похідної по
називається оператором частинної похідної по 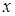 . Під добутком цього оператора на функцію
. Під добутком цього оператора на функцію 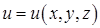 розумітимемо частинну похідну
розумітимемо частинну похідну  , тобто
, тобто  . Аналогічно,
. Аналогічно,  і
і  – оператори частинних похідних по
– оператори частинних похідних по 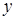 і по
і по  .
.
Введемо векторний оператор «набла» або оператор Гамільтона:
 .
.
За допомогою цього символічного (операторного) «вектора» зручно записувати і виконувати операції векторного аналізу.
У результаті множення вектора  на скалярну функцію
на скалярну функцію 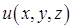 отримуємо
отримуємо 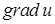 :
:
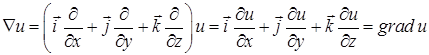 .
.
Скалярний добуток вектора  на вектор – функцію
на вектор – функцію  дає
дає 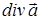 :
:
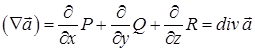 .
.
Векторний добуток вектора  на вектор – функцію
на вектор – функцію 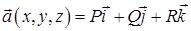 дає
дає  :
:
 .
.
Нестаціонарні поля
Нехай в області  визначено нестаціонарне скалярне поле
визначено нестаціонарне скалярне поле 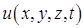 : величина
: величина 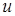 є функцією точки
є функцією точки 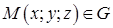 і часу
і часу  . Приклад такого поля – змінний з часом розподіл температури в будь-якому середовищі (наприклад, в потоці рідини). Розглянемо точку
. Приклад такого поля – змінний з часом розподіл температури в будь-якому середовищі (наприклад, в потоці рідини). Розглянемо точку  , яка рухається в області
, яка рухається в області  (частинку рідини). Координати точки (частинки) змінюються з часом за відомим законом
(частинку рідини). Координати точки (частинки) змінюються з часом за відомим законом  . Величина
. Величина 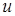 в рухомій точці
в рухомій точці 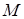 є складеною функцією
є складеною функцією 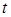 :
:
 .
.
Обчислимо похідну по  цієї функції (вона називається повною похідною). За правилом диференціювання складеної функції знаходимо
цієї функції (вона називається повною похідною). За правилом диференціювання складеної функції знаходимо
 .
.
Вводячи в точці 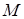 вектор швидкості
вектор швидкості 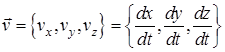 , отримуємо
, отримуємо
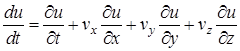
Або
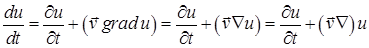 .(11)
.(11)
Аналогічно, якщо в області  задано нестаціонарне векторне поле
задано нестаціонарне векторне поле  , то для рухомої точки
, то для рухомої точки  векторна величина
векторна величина  є складеною функцією
є складеною функцією  :
: 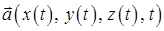 . Повну похідну по
. Повну похідну по  для кожної координати вектор – функції
для кожної координати вектор – функції  можна обчислити за формулою (11). Помноживши результати на базисні вектори
можна обчислити за формулою (11). Помноживши результати на базисні вектори  і складаючи, отримуємо
і складаючи, отримуємо
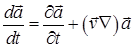 .(12)
.(12)
У формулах (11) і (12) доданки  і
і  виражають швидкості зміни величин
виражають швидкості зміни величин  та
та  з часом при фіксованих координатах, тобто характеризують локальні зміни цих величин, і тому називаються локальними похідними. Доданки
з часом при фіксованих координатах, тобто характеризують локальні зміни цих величин, і тому називаються локальними похідними. Доданки  і
і  утворюються за рахунок зміни координат точки, її руху (конвекції). Тому ці доданки у виразах повних похідних називаються конвективними похідними.
утворюються за рахунок зміни координат точки, її руху (конвекції). Тому ці доданки у виразах повних похідних називаються конвективними похідними.
Локальні похідні характеризують нестаціонарність розглянутого поля у даній точці простору. Конвективні похідні характеризують неоднорідність поля у даний момент часу.
Размещено на Allbest.ru
 2020-04-20
2020-04-20 253
253