2020-04-20
124
В даній курсовій роботі ми дослідили еліптичний інтеграл першого роду при різних значеннях аргументу k (при 0≤k≤1) різними методами: Сімпсона, Нютона-Котеса, Чебишева. В результаті ми отримали таблицю значень, з якої можна спостерігати як впливає значення коефіцієнта на сам інтеграл. Для проміжку інтегрування (0;1) та для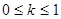 
при кроці h=0.05 дані зведені в таблицю 4.1.
Таблиця 4.1 Результати експерементальних досліджень
| k | f(k,φ) | ||
| м-д Сімпсона | м-д Нютона-Котеса | м-д Чебишева | |
| 0.00 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 | 1.00000000 0.99863505 0.99452144 0.98760122 0.97777176 0.96487713 0.94869113 0.92888802 0.90499073 0.87626529 | 1.00000000 0.99863511 0.99452150 0.98760098 0.97777128 0.96487653 0.94868988 0.92888618 0.90498829 0.87626225 | 1.00000000 0.99863511 0.99452144 0.98760092 0.97777128 0.96487647 0.94868994 0.92888629 0.90498835 0.87626213 |
Як видно з таблиці 4.1 коефіціент k впливає на значення інтегралу обернено-пропорційно. Тобто при збільшені коефіцієнта значення функції зменшується.
Оцінка похибок отриманих результатів
Для аналізу похибок необхідно знати точне та наближене значення. Для функції тестування провести аналіз похибки набагато простіше, адже точне значення знаходиться дуже легко. Так наприклад при обчисленні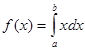 
точні значення інтегралу взагалі можна обраховувати „в умі”. Для тестування функції 
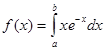ми скористаємось допомогою середовища “MathCad”
|
|
|
Знайдемо похибку трьох методів для першого і другого тесту, що описані в розділі 3.2. При обчисленні наближеними методами (програмою) ми отримали результати, приведені в таблиці 3.1 та 3.2. Розраховані похибки обчислень тесту №1 приведені в таблиці 5.1 та 5.2. Похибки для тесту №2 приведені в таблиці 5.3 і 5.4.
Таблиця 5.1 Оцінка абсолютних похибок тесту №1
| x | Абсолютна похибка Δ | ||
| Сімпсона | Нютона-Котеса | Чебишева | |
| 0.00 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 1.00 | 0.000 0.000 0.000 0.000 0.000 0,00000003 0,00000004 0,00000006 0.00000008 0.00000009 0.00000018 | 0.000 0.000 0.000 0.000 0,00000001 0.000 0,00000001 0.00000005 0.00000005 0.00000009 0.00000018 | 0.000 0.000 0.000 0.000 0,00000001 0.000 0,00000001 0.00000005 0.00000005 0.00000009 0.00000012 |
Таблиця 5.2 Оцінка відносних похибок тесту №1
| x | Відносна похибка ε, % | ||
| Сімпсона | Нютона-Котеса | Чебишева | |
| 0.00 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 1.00 | 0.000 0.000 0.000 0.000 0.000 0.000024 0.000031 0.000038 0.000041 0.000044 0.000083 | 0.000 0.000 0.000 0.000 0,0000125 0.000 0,0000125 0.000034 0.000038 0.000044 0.000083 | 0.000 0.000 0.000 0.000 0,0000125 0.000 0,0000125 0.000034 0.000034 0.000038 0.000066 |
Таблиця 5.3 Оцінка абсолютних похибок тесту №2
| x | Абсолютна похибка Δ | ||
| Сімпсона | Нютона-Котеса | Чебишева | |
| 0.00 0.40 0.80 1.20 1.60 2.00 2.40 2.80 3.20 3.60 4.00 | 0.000 0.00000069 0.00000111 0.00000135 0.00000143 0.00000239 0.0000166 0.0000170 0.0000158 0.0000157 0.0000159 | 0.000 0.00000001 0.00000001 0.00000001 0.00000001 0.00000055 0.00000220 0.00000718 0.00001946 0.000004585 0.000009672 | 0.000 0.000 0.00000002 0.00000004 0.000 0.00000003 0.000000150 0.000000498 0.000001380 0.000003253 0.000006886 |
|
|
|
Таблиця 5.4 Оцінка відносних похибок тесту №2
| x | Відносна похибка ε, % | ||
| Сімпсона | Нютона-Котеса | Чебишева | |
| 0.00 0.40 0.80 1.20 1.60 2.00 2.40 2.80 3.20 3.60 4.00 | 0.000 0.0011 0.00058 0.00040 0.000301 0.0004434 0.00024 0.00226 0.00192 0.00192 0.00192 | 0.000 0.000 0.000 0.000 0.000 0.0000932 0.0003184 0.000944 0.00137 0.0052 0.00107 | 0.000 0.000 0.000 0.000 0.0000118 0.0000091 0.0002697 0.000655 0.00168 0.000373 0.0007651 |
Отже як видно з приведеного аналізу найменшу похибку має метод Чебишева, тобто він є найточнішим
