Скалярное произведение векторов.
Определение 1. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначение 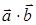 или
или 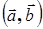 :
:
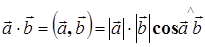 .
.
Алгебраические свойства скалярного произведения.
1°. 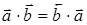 − выполняется коммутативный закон;
− выполняется коммутативный закон;
2°. 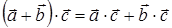 − выполняется дистрибутивный закон;
− выполняется дистрибутивный закон;
3°. 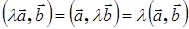 − константу можно выносить за знак скалярного произведения;
− константу можно выносить за знак скалярного произведения;
4°. 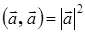 − скалярный квадрат вектора равен квадрату его модуля;
− скалярный квадрат вектора равен квадрату его модуля;
5°. 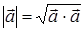 .
.
Пример.
Найти 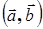 и
и 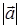 , если
, если 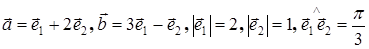 .
.
Решение.
 ,
,
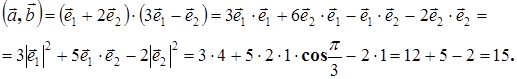
Ответ: 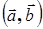 =15,
=15, 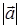 =
= 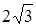 .
.
Скалярное произведение в декартовой системе координат.
Скалярное произведение базисных ортов декартовой системы:
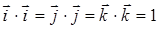 ,
,
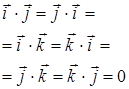 , т.к. все орты взаимно перпендикулярны, а
, т.к. все орты взаимно перпендикулярны, а 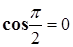 .
.
Теорема 1. Если векторы 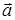 и
и 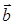 заданы своими координатами в декартовой системе координат, то их скалярное произведение равно сумме произведений соответствующих координат. Т.е.
заданы своими координатами в декартовой системе координат, то их скалярное произведение равно сумме произведений соответствующих координат. Т.е.
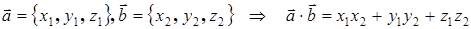 .
.
Доказательство:
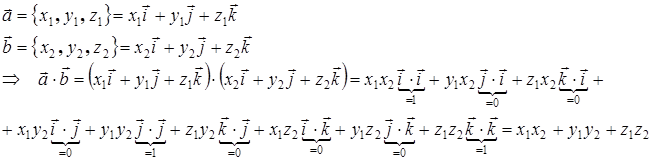 что и требовалось доказать.
что и требовалось доказать.
Геометрические приложения скалярного произведения.
1°. 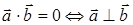 − условие ортогональности двух векторов.
− условие ортогональности двух векторов.
2°. 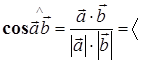 в декартовом базисе
в декартовом базисе 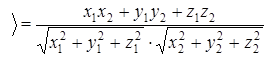 .
.
3°. 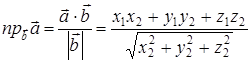 .
.
Пример.
Найти угол между векторами 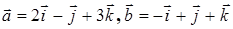 .
.
Решение.
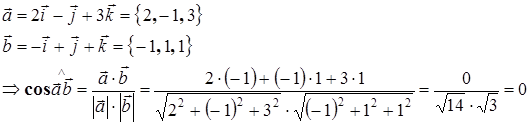
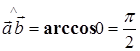
Ответ: угол между векторами равен 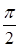 .
.
Векторное произведение векторов.
Определение 2. Упорядоченная тройка векторов называется правой, если с конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки
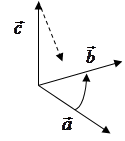 тройка
тройка 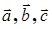 − правая.
− правая.
Определение 3. Упорядоченная тройка векторов называется левой, если с конца третьего вектора кратчайший поворот от первого ко второму виден по часовой стрелке
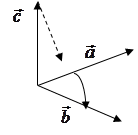 тройка
тройка 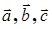 − левая
− левая
Очевидно, что если в тройке поменять местами хотя бы пару векторов, то ориентация тройки изменится. Поэтому мы и говорим об упорядоченности.
Определение 4. Векторным произведением вектора 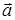 на вектор
на вектор 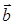 называется вектор
называется вектор  , обладающий следующими свойствами:
, обладающий следующими свойствами:
1) длина вектора  равна произведению длин перемножаемых векторов на синус угла между ними;
равна произведению длин перемножаемых векторов на синус угла между ними;
2) вектор  перпендикулярен каждому из перемножаемых векторов;
перпендикулярен каждому из перемножаемых векторов;
3) упорядоченная тройка векторов  − правая.
− правая.
Обозначение 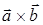 или
или 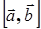 :
:
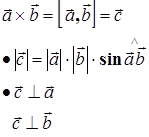
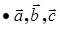 − правая.
− правая.
Алгебраические свойства скалярного произведения.
1°. 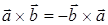 − коммутативный закон не выполняется.
− коммутативный закон не выполняется.
2°. 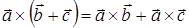 − дистрибутивный закон выполняется.
− дистрибутивный закон выполняется.
3°. 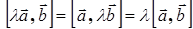 − константу можно выносить за знак векторного произведения.
− константу можно выносить за знак векторного произведения.
4°. 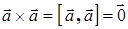 − векторный квадрат любого вектора равен нулю.
− векторный квадрат любого вектора равен нулю.
Пример.
Упростить выражение 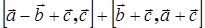 .
.
Решение.
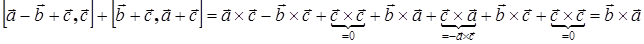 Ответ:
Ответ: 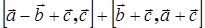 =
= 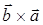 .
.
Векторное произведение в декартовой системе координат.
Векторное произведение базисных ортов декартовой системы удобно выполнять так:
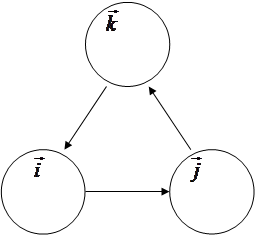 по схеме: в противоположном направлении:
по схеме: в противоположном направлении:
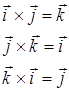
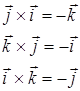
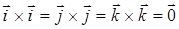 .
.
Теорема 2. Если векторы 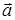 и
и 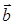 заданы своими координатами в декартовой системе координат, то их векторное произведение равно значению обобщенного определителя, в котором элементами первой строки являются базисные орты, элементы второй строки – координаты первого из перемножаемых векторов, а элементы третьей строки – координаты второго вектора.
заданы своими координатами в декартовой системе координат, то их векторное произведение равно значению обобщенного определителя, в котором элементами первой строки являются базисные орты, элементы второй строки – координаты первого из перемножаемых векторов, а элементы третьей строки – координаты второго вектора.
Т.е., если  , то
, то 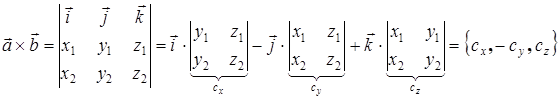 .
.
(без доказательства)
Геометрические приложения векторного произведения.
1°. Модуль вектора 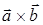 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах 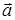 и
и 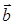 .
.
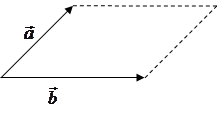
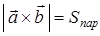
2°. 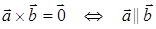 − условие коллинеарности двух векторов.
− условие коллинеарности двух векторов.
Замечание. В таком виде условие коллинеарности используется редко, обычно мы считаем, что векторы коллинеарны, если их координаты пропорциональны. И наоборот:
если  , то
, то 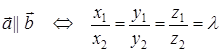 .
.
При этом, если λ > 0, то векторы сонаправлены 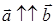 и угол между ними равен нулю, если же λ < 0, то векторы противоположно направлены
и угол между ними равен нулю, если же λ < 0, то векторы противоположно направлены 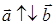 и угол между ними равен π.
и угол между ними равен π.
Пример.
Найти площадь треугольника АВС, заданного координатами своих вершин А (2, 1, 0), В (3, -2, 1), С (0, 1, 3).
Решение.
Площадь треугольника АВС  равна половине площади параллелограмма ABCD, построенного на векторах
равна половине площади параллелограмма ABCD, построенного на векторах 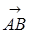 и
и 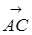 . Следовательно, его площадь равна половине модуля векторного произведения этих векторов. Координаты векторов:
. Следовательно, его площадь равна половине модуля векторного произведения этих векторов. Координаты векторов: 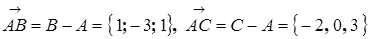 .
.
Их векторное произведение равно:
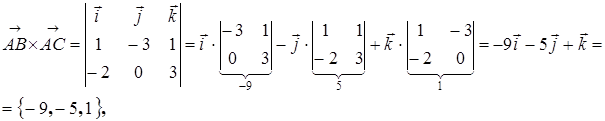
Модуль этого вектора равен:
 , следовательно, площадь треугольника АВС равна
, следовательно, площадь треугольника АВС равна 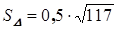 .
.
Ответ: 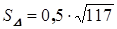 .
.
 2020-04-20
2020-04-20 293
293







