2020-04-20
127
Реферат
В работе реализуется нахождение решения одной задачи на тему максимизации функций многих переменных. При этом рассматриваются методы дихотомии и покоординатного спуска.
Пояснительная записка к курсовой работе состоит из двух основных частей: теоретической и практической.
В теоретической части рассматривается поиск максимума одной функции многих переменных методом покоординатного спуска и с помощью метода дихотомии.
Практическая часть содержит разработку программного обеспечения для решения заданной задачи выше указанными методами, реализованную на языке С++.
Объем пояснительной записки: 1
Количество рисунков: 3
Количество используемых источников: 3
Содержание
Введение
1. Постановка задачи
2. Решение задачи с использованием метода дихотомии
2.1 Описание метода дихотомии
2.2 Алгоритм решения
3. Решение задачи с использованием метода покоординатного спуска
3.1 Описание метода покоординатного спуска
3.2 Алгоритм решения
Заключение
|
|
|
Список используемой литературы
Приложение 1. Листинг программы№1
Приложение 2. Листинг программы №2
Приложение 3. Листинг программы №3
Приложение 4. Результаты работы программы №1
Приложение 5. Результаты работы программы №3
Введение
В работе рассмотрены способы нахождения таких значений аргументов, при которых исходная функция максимальна, а вспомогательная (от которой зависит исходная) – минимальна. В параграфе 2 изложено решение задачи с использованием метода дихотомии. В параграфе 3 произведено исследование задачи методом покоординатного спуска.
Постановка задачи
Исходная функция имеет вид:
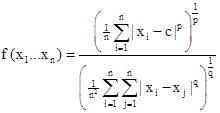, где:
xi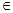 
R –– параметры исходной функции;
p, q 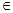R –– некоторые параметры удовлетворяющие условию 1<p 
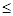q<∞;
с=c(x1…xn) –– вспомогательная функция, записанная в неявном виде
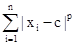→min.
Задача:
Найти xi*,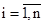 
: f(x1*…xn*)= 
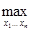f(x1…xn).
Выполним следующую замену: xi=axi+b, 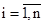. При этом значение функции не изменится:
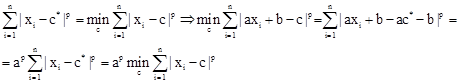
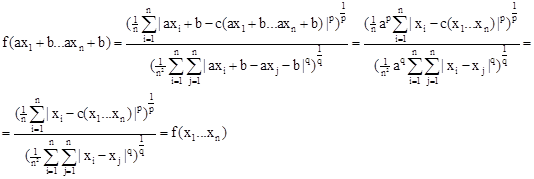
Таким образом, исходную область определения функции можно сузить до xi 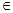R[0;1]. Так как знаменатель не должен быть равным нулю, то xi≠xj 
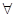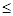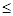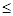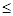i≠j. Но тогда все параметры можно расположить по возрастанию: x1 x2 … xi xi+1 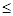… 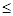xn, а выбором a и b можно привести x1=0, xn=1.
Далее будем рассматривать задачу от n-2 переменных, т.к. x1 и xn являются константами.
Решение задачи с использованием метода дихотомии
