Средние структурные показатели

Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным её расчет не может быть выполнен.

Структурные средние, в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определёнными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.

Наиболее широко применяются в статистике такие разновидности структурных средних, как мода и медиана.

1). Мода (Мо) представляет собой значение признака (варианты), повторяющееся в изучаемой совокупности с наибольшей частотой.

В дискретном ряду мода – это варианта с наибольшей частотой.

В интервальном ряду модой считают центральную варианту модального интервала. В пределах интервала надо определить то значение признака, который обладает наибольшей частотой. Для определения моды используют следующую формулу:

, где:

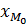- нижняя граница модального интервала;

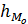- величина модального интервала;

- частота модального интервала;

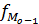- частота, следующая за модальным интервалом;

- частота, предшествующая модальному интервалу.

Мода обладает определённой устойчивостью к вариации признака. Если в совокупности первичных признаков нет повторяющихся значений, то для определения моды проводят группировку.

Модальные показатели широко используются в экономическом анализе. Например, при изучении рыночной конъюнктуры обычно рассчитывается модальная цена, т. е. цена, по которой продаётся максимальное количество товаров того или иного вида.

2). Медианой (Ме) называют значение признака, приходящееся на середину упорядоченной (ранжированной в возрастающем или убывающем порядке) совокупности. Медиана делит ряд на две одинаковые части таким образом, чтобы по обе её стороны находилось одинаковое число единиц совокупности. В итоге у одной половины единиц совокупности значение признака больше медианного уровня, а у другой – меньше его.

В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера и значения варианты у этого номера.

В дискретном ряду с нечётным числом членов медианой является варианта, расположенная в центре ряда. Её порядковый номер определяется по формуле:

В дискретном ряду с чётным числом членов медианой будет являться среднее значение между двумя вариантами, определёнными по формуле:

Нахождение медианы в интервальных вариационных рядах требует предварительного определения интервала в котором находится медиана, т. е. медианного интервала – этот интервал характеризуется тем, что его накопленная частота равна или превышает половину общей суммы всех частот совокупности.

В зависимости от этого медиану определяют по формуле:

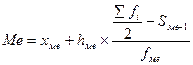
где - нижняя граница (начальное значение) медианного интервала;

- величина медианного интервала;

- сумма частот ряда;

- сумма накопленных частот до частоты медианного интервала;

- частота медианного интервала.

Также в интервальных вариационных рядах медиана может быть найдена с помощью кумуляты как значение признака, для которого

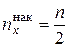или .

Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы всегда меньше, чем сумма отклонений вариант от любой другой величины: .

В симметричных рядах имеет место следующее соотношение моды, медианы и средней арифметической: .

В случае, если , имеет место левосторонняя асимметрия ряда.

В случае, если , имеет место правосторонняя асимметрия ряда.

1 2 3

1 – распределение с левосторонней асимметрией

2 – распределение с правосторонней асимметрией

3 – нормальное (симметричное) распределение

Мода и медиана,в отличие от степенных средних, являются конкретными характеристиками совокупности. Медиана – характеризует центр, вычисляется проще и не чувствительна к концам интервала. Мода – наиболее вероятное значение в изучаемой совокупности (например, наиболее возможные результаты).

Графически отобразить моду по гистограмме можно следующим образом: нужно взять столбец, имеющий наибольшую высоту и из его левого верхнего угла провести отрезок в угол последующего столбца, а из правого угла – в верхний правый угол предыдущего столбца, абсцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности. Медиану приближенно можно определить графически – по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения и есть медиана (рисунок 1).

Рис. 1. Графическое отображение интервального вариационного ряда

3). Квартили – значения признака, делящие ранжированную совокупность на четыре равные части.

Различают нижний квартиль 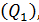отделяющий ¼ часть совокупности с наименьшими значениями признака, и верхний квартиль , отсекающий ¼ часть с наибольшими значениями признака. Средний квартиль совпадает с медианой.

Квартили рассчитываются аналогично медиане, только сумма часто берётся с другими коэффициентами – или .

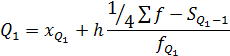
- нижняя граница интервала, содержащего нижний (верхний) квартиль;

h - величина интервала;

- накопленная частота интервала, предшествующего интервалу, содержащему нижний (верхний) квартиль;

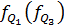- частота интервала, содержащего нижний (верхний) квартиль.

4). Квинтили – значения признака, делящие ряд на пять равных частей.

5). Децили – варианты, делящие ранжированный ряд на десять равных частей.

6). Перцентили – значения признака, делящие ряд на 100 равных частей.

Схема вычисления приведённых показателей аналогична схеме расчёта квартилей.

Пример 3.1.

Определить медиану, если:

Стаж рабочих, лет	Численность рабочих, чел.	Накопленные частоты
0-5	146	146
5-10	495	641
10-15	237	878
15-20	103	981
20 и более	19	1000
Всего:	1000

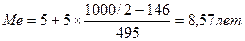
Вывод: из 1000 рабочих 500 чел. имеет стаж работы меньше 8,57 лет.

Пример 3.2.

Имеются данные о распределении работников предприятия по уровню среднемесячной заработной платы:

№ группы	Заработная плата, ден. ед.	Число работников, чел.	Сумма накопленных частот
1 2 3 4 5 6	500-600 600-700 700-800 800-900 900-1000 свыше 1000	10 30 70 60 25 5	10 40 110 - - -

Определить модальный размер и медианный интервал заработной платы.

Решение: Первоначально по наибольшей частоте признака определим модальный интервал. Наибольшее число работников (70 человек) имеют заработную плату в интервале 700-800 ден. ед., который и является модальным.

ден. ед.

Модальный доход показывает, что большинство работников получали заработную плату в размере 780 ден. ед.

Определяем медианный интервал, в котором находится порядковый номер медианы. Для этого подсчитаем сумму частот накопленным итогом до числа, превышающего половину объема совокупности (200/2=100).

В графе «сумма накопленных частот» значение 110 соответствует интервалу 700-800. Это и есть медианный интервал, в котором находится медиана.

ден. ед.

Из расчета видно, что половина работников предприятия имеют заработную плату до 785,7 ден. ед., а половина – выше этой суммы.

Пример 3.3

По результатам зимней экзаменационной сессии студентов экономического факультета очной формы обучения было получено следующее распределение оценок:

Балл оценки знаний студентов	2	3	4	5	Итого
Число оценок, полученных студентами	6	75	120	99	300

Определить:

1) средний балл оценки знаний студентов;

2) модальный балл успеваемости;

3) медианное значение балла успеваемости.

Сделать вывод о характере данного распределения баллов.

Решение:

1). Средний балл оценки знаний студентов рассчитывается по формуле средней арифметической взвешенной, где в качестве весов выступает количество полученных оценок:

2). Модальным баллом успеваемости является 4, так как именно эта оценка в дискретном ряду распределения имеет наибольшую частоту – 120.

3). Так как данный ряд распределения является дискретным с чётным количеством единиц (300), то медиана расположена между 150 и 151 единицей совокупности. Медианный балл успеваемости равен 4, так как количество студентов, сдавших сессию на 2 и 3, равно 81 чел., что меньше 150, а количество студентов, сдавших сессию на 2, 3 и 4, равно 201 чел., что больше 151.

Поскольку значения средней, моды и медианы оказались равными друг другу, то распределение оценок студентов является симметричным.

Пример 3.4.

Дано следующее распределение студентов факультета по росту:

Рост, см.	Численность студентов, чел.
До 162 162 – 166 166 – 170 170 – 174 174 – 178 178 – 182 182 и более	30 55 90 125 130 50 20
Итого:	500

Определить среднюю величину, моду и медиану роста студентов.

Решение:

1). Данный ряд распределения является интервальным с величиной интервала, равной 4 см. Тогда нижняя граница первого интервала составляет: 162 – 4 = 158 см, а верхняя граница последнего интервала равна: 182 + 4 = 186 см.

Для расчёта среднего роста студентов будем брать середины каждого из интервалов: 160, 164, 168, 172, 176, 180 и 184 см. Подставляем данные значения в формулу средней арифметической взвешенной:

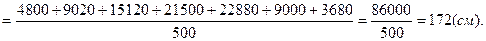
2). Модальный интервал – 174 – 178 см, так он имеет наибольшую частоту по сравнению с остальными интервалами – 130 чел.

Рассчитываем значение моды:

3). Для определения медианного интервала рассчитаем накопленные частоты:

Рост, см.	Накопленная частота численности студентов, чел.
До 162 162 – 166 166 – 170 170 – 174 174 – 178 178 – 182 182 и более	30 30+55=85 85+90=175 175+125=300 300+130=430 430+50=480 480+20=500

Полусумма частот – 250, значит медианный интервал – 170 – 174, так как его накопленная частота 300 больше 250.

Рассчитываем значение медианы: